二叉树定义:
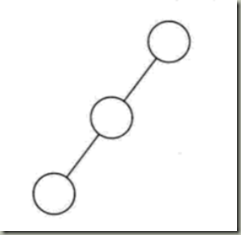
1、斜树
所有的结点都只有左子树(左斜树),或者只有右子树(右斜树)。

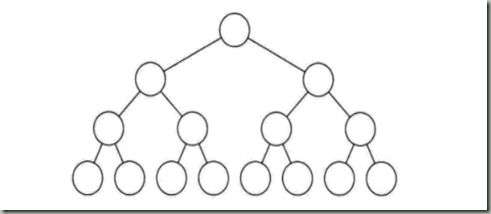
2、满二叉树
所有的分支结点都存在左子树和右子树,并且所有的叶子结点都在同一层上。
3、完全二叉树
对一棵具有n个结点的二叉树按层序排号,如果编号为i的结点与同样深度的满二叉树编号为i结点在二叉树中位置完全相同,就是完全二叉树。满二叉树必须是完全二叉树,反过来不一定成立。

4、二叉搜索树(BST)
它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
5、平衡二叉树(AVL)
它或者是一棵空树,或者是具有下列性质的二叉树:它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,同时,平衡二叉树必定是二叉搜索树,反之则不一定。

二叉树遍历:

1、前序遍历
基本思想:先访问根结点,再先序遍历左子树,最后再先序遍历右子树。即 根—左—右。
如上图遍历结果为:ABDHECFG
2、中序遍历
基本思想:先中序遍历左子树,然后再访问根结点,最后再中序遍历右子树。即 左—根—右。
如上图遍历结果为:HDBEAFCG
3、后序遍历
基本思想:先后序遍历左子树,然后再后序遍历右子树,最后再访问根结点。即 左—右—根。
如上图遍历结果为:HDEBFGCA
~~~ 可能有些新手,对于树的节点一多,就很难分清遍历到底应该怎么走。其实很简单,把树分解成各个子树就好办了。只要是非叶子节点,那就可以把它看做是根节点,然后也就是只有根左右 3 个节点,
例如上图,先分为左右子树
ps:前序遍历,根—左—右,即从根节点A往左子树查找,只要左子树的左边有节点,就不要管左子树的右边,可得出 ABDH ,左边没有节点的时候,再在左子树右边从下向上查找,如果右边节点又有子节点,那么继续重复上面的步骤即可。如上图,H节点是叶子节点,左边已无节点,从下向上找右边,也就是E,得到 ABDHE,当然了,如果E下面有E1和E2左右两个节点,那么应该得到A B D H E E1 E2,相当于E是根节点,按照 根—左—右 就行了,左边查完,走右边就行了,右边得到ACFG,合并之后即ABDHECFG
























 940
940

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








