数据结构：二叉树的遍历

最新推荐文章于 2023-10-30 22:33:27 发布
最新推荐文章于 2023-10-30 22:33:27 发布
阅读量821 收藏 9
点赞数 1
CC 4.0 BY-SA版权
分类专栏： 习题 文章标签： 二叉树
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/e_t_e_r_n_i_t_y/article/details/111699180
该博客围绕二叉树实验展开，目的是让学生理解二叉树链式存储、遍历算法及递归含义。实验内容包括实现二叉树创建、多种遍历算法及求深度，非递归算法需自行实现栈和队列操作。还给出了测试用例及设计思想，涉及创建、遍历和求深度的具体思路。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

（1）实验目的
通过该实验，使学生理解二叉树的链式存储，掌握二叉树的几种遍历算法，并通过该实验使学生理解递归的含义，掌握C语言编写递归函数的方法和注意事项。
（2）实验内容
实现教材中算法6.4描述的二叉树创建算法，在此基础上实现二叉树的先序、后序递归遍历算法、两种非递归中序遍历、层序遍历、求二叉树的深度。注意：在非递归算法中用到栈和队列时，不要调用系统的栈和队列，需要自己实现栈和队列的操作。
（3）参考界面

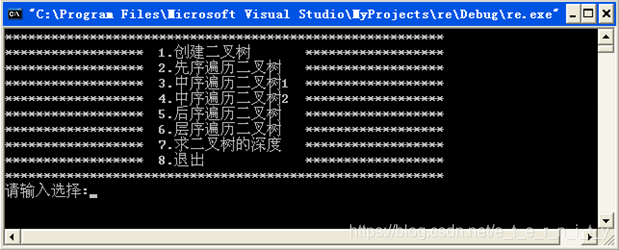
在这里插入图片描述
（4）验收/测试用例

  • 创建

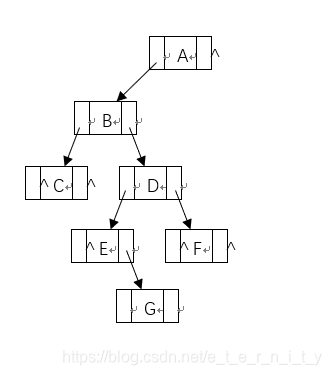
输入 ：ABC$ $ DE$ G $ $ F$ $ $ ($表示空格)
该输入对应的树如图所示

  • 先序 屏幕输出 A B C D E G F
  • 后序 屏幕输出 C G E F D B A
  • 中序 屏幕输出 C B E G D F A
    (两种中序非递归还需看源代码)
  • 层序 屏幕输出 A B C D E F G
  • 深度 屏幕显示 深度为5
  • 另外自己画出一棵树，再测试一遍。
    在这里插入图片描述
    设计思想
    创建二叉树：按先序次序输入二叉树中结点得值（一个字符），空格字符表示空树，
    构造二叉链表表示的二叉树T。
    先序遍历：采用二叉链表存储结构，递归
    先序遍历二叉树T，对每个结点调用函数Visit一次且仅一次。
    一旦visit（）失败，则操作失败。
    后序遍历：同先序；
    非递归中序遍历：先遍历左子树，然后再遍历根节点，最后遍历右子树，
    故需要一个空间存放遍历左子树时经过的节点，且
    后遍历的节点先调用，故该空间可用栈来存放。
    层序遍历：树是肯定没发直接将一层的节点挨个遍历，它只能将一个树枝上
    的节点遍历完后再去遍历其他节点（否则不容易检查节点是否被遍历）
    显而易见，这肯定需要另一个空间存储该树枝上该层下的节点
    并且先放进去的节点是原节点下一层的节点所以最好先取出来
    故该存储空间选用队列 继续分析下去， 当根节点进入又推出时，该 左右孩子都进入了，此时需要判断一下其是否有左右孩子。
    求二叉树深度：递归
    主要源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define OK 1
#define ERROR 0
#define OVERFLOW -2
//--------------二叉树的二叉链表存储表示------------------- 
#define INIT_SIZE 100     //初始分配量 
#define CREMENT 10        //分配增量

typedef int status;     //status是函数的类型，其值是函数结果状态代码。
typedef int TElem;      //自定义

/*
    二叉链表 
    data：存储数据或者权值；
	lchild,rchild ：左右孩子指针 
*/
typedef struct BiTNode{
	TElem data;
	struct BiTNode *lchild,*rchild;//左右孩子指针 
}BiTNode,*BiTree;

//链队列 
typedef struct QNode{
	BiTree data;
	struct QNode *next;
}QNode,*Queue;

typedef struct {
	Queue front;
	Queue rear;
}LQueue;

//顺序栈 
typedef struct {
	BiTree *base;  
	BiTree *top;
	int stacksize;     
}SqStack;   

//---------------基本操作的函数原型说明------------
 
//二叉树 
status CreatBiTree(BiTree &T);
       //按先序次序输入二叉树中结点得值（一个字符），空格字符表示空树，
	   //构造二叉链表表示的二叉树T。
status visit(TElem e);
       //对结点进行访问 
status PreOrderTraverse(BiTree T,status(*visit)(TElem e));
       //采用二叉链表存储结构，递归 
	   //先序遍历二叉树T，对每个结点调用函数Visit一次且仅一次。
	   //一旦visit（）失败，则操作失败。
status InOrderTraverse(BiTree T,status(*visit)(TElem e));
       //同上，中序遍历，递归 
status PostOrderTraverse(BiTree T,status(*visit)(TElem e));
       //同上，后序遍历 ，递归 
status InOrderTraverse1(BiTree T,status(*visit)(TElem e));
       //非递归中序遍历1 
status InOrderTraverse2(BiTree T,status(*visit)(TElem e));
       //非递归中序遍历2 
status LevelOrderTraverse(BiTree T,status(*visit)(TElem e));
       //同上，层序遍历
status BiTreeDepth(BiTree T);	
       //求二叉树深度    
 
 //栈      
status InitStack(SqStack &S);
       //创建栈 
status Push(SqStack &S,BiTree T); 
       //入栈 
status StackEmpty(SqStack S);
       //栈判空 
status GetTop(SqStack S,BiTree &e);
       //取栈顶元素 
status Pop(SqStack &S,BiTree &e); 
       //出栈 

//队列函数
status InitQueue(LQueue &L);
       //初始化队列 
status QueueEmpty(LQueue L);
       //队列判空 
status EnQueue(LQueue &L,BiTree T);
       //入队列 
status DeQueue(LQueue &L,BiTree &e);
       //出队列 
//---------------主函数---------------------------- 
int main(){
	int i;
	BiTree T = NULL;
	
	int choice;
	while (1){
		//菜单
		printf("--------------------------------------------------------------\n");
		printf("\t\t\t 1---创建一个二叉树\n");
		printf("\t\t\t 2---先序遍历二叉树\n");
		printf("\t\t\t 3---中序遍历二叉树1\n");
		printf("\t\t\t 4---中序遍历二叉树2\n");
		printf("\t\t\t 5---后序遍历二叉树\n");
		printf("\t\t\t 6---层序遍历二叉树\n");
		printf("\t\t\t 7---求二叉树的深度\n");	
		printf("\t\t\t 退出，输入一个负数！");
		printf("\n");
		printf("--------------------------------------------------------------\n");
		printf("\n");
		printf("请输入你需要的操作：\n");
		//退出
		scanf("%d",&choice);
		if(choice<=0){
			printf("已退出\n");
			return 0;
		} 
		switch (choice){
			case 1:
				i = CreatBiTree(T);
				if(i == -2){
					printf("空间开辟失败\n");
				}else{
					printf("创建成功！\n");
				}
				break;
			case 2:
				i = PreOrderTraverse(T,visit);
				if(i == 1){
					printf("\n先序遍历成功！\n");
				}else{
					printf("先序遍历失败！\n");
				}
				break;
			case 3:
				
				i == InOrderTraverse1(T,visit);
				if(i == 1){
					printf("\n中序遍历成功！\n");
				}else{
					printf("中序遍历失败！\n");
				}
				
				break;
			case 4:
				i == InOrderTraverse2(T,visit);
				if(i == 1){
					printf("\n中序遍历成功！\n");
				}else{
					printf("中序遍历失败！\n");
				}
				break;
			case 5:
				i == PostOrderTraverse(T,visit);
				if(i == 1){
					printf("\n后序遍历成功！\n");
				}else{
					printf("后序遍历失败！\n");
				}
				break;
			case 6:
				i == LevelOrderTraverse(T,visit);
				if(i == 1){
					printf("\n层序遍历成功！\n");
				}else{
					printf("层序遍历失败！\n");
				}
				break;
			case 7:
				i = BiTreeDepth(T);
				if(i == 0){
					printf("该树是空树\n");
				} else{
					printf("该树的深度为%d\n",i);
				}
				break;
			default:
				printf("选择失败！请重新选择！\n");
				break; 	 	 	 			
		}
		system("pause");   //请按任意键结束 
		system("cls");     //清屏 
	}
	return 0;
} 

//---------------基本操作的算法描述----------------
status CreatBiTree(BiTree &T){ 
    //按先序次序输入二叉树中结点得值（一个字符），空格字符表示空树，
	//构造二叉链表表示的二叉树T。
	char ch = ' ';
	printf("请输入结点值（空格表示空）：");
	getchar();    //清空缓存区，否则scanf会直接读取选择后的回车键。 
	scanf("%c",&ch);
	if(ch ==' '){
		T = NULL;
	}else {
		T = (BiTNode*)malloc(sizeof(BiTNode));
		if(!T){
			return OVERFLOW;
		}
		T->data = ch;     //生成该节点值，第一个则生成根节点 
		CreatBiTree(T->lchild);//构造左孩子 
		CreatBiTree(T->rchild);//构造右孩子 
	}
	return OK; 
} 

status visit(TElem e){
	//对结点进行访问,有值则输出该值返回OK，为空则输出$返回ERROR 
	 if(e){
	 	printf("%c",e);
	 	return OK;
	 }else{
	 	return ERROR;
	 }
};
 
//递归调用的三种遍历     
status PreOrderTraverse(BiTree T,status(*visit)(TElem e)){
	//采用二叉链表存储结构，Visit是对结点操作的应用函数。
	//先序遍历二叉树T，对每个结点调用函数Visit一次且仅一次。
	//一旦visit（）失败，则操作失败。
	if(T){
		if(visit(T->data)==1){
			if(PreOrderTraverse(T->lchild,visit) == 1){
				if(PreOrderTraverse(T->rchild,visit) == 1){
					return OK;
				}
			}
		}
		return ERROR;
	}else{
		return OK;
	}
}
  
status InOrderTraverse(BiTree T,status(*visit)(TElem e)){
	//采用二叉链表存储结构，Visit是对结点操作的应用函数。
	//中序遍历二叉树T，对每个结点调用函数Visit一次且仅一次。
	//一旦visit（）失败，则操作失败。
	if(T){
		if(InOrderTraverse(T->lchild,visit) ==1){
			if(visit(T->data)== 1){
				if(InOrderTraverse(T->rchild,visit) == 1){
					return OK;
				}
			}
		}
		return ERROR;
	}else{
		return OK;
	}
}

status PostOrderTraverse(BiTree T,status(*visit)(TElem e)){
	//采用二叉链表存储结构，Visit是对结点操作的应用函数。
	//后序遍历二叉树T，对每个结点调用函数Visit一次且仅一次。
	//一旦visit（）失败，则操作失败。
	if(T){
		if(PostOrderTraverse(T->lchild,visit) ==1){
			if(PostOrderTraverse(T->rchild,visit) == 1){
				if(visit(T->data) == 1){
					return OK;
				}
			}
		}
		return ERROR;
	}else{
		return OK;
	}
}

//非递归调用的两种中序遍历 
status InOrderTraverse1(BiTree T,status(*visit)(TElem e)){
	//非递归中序遍历1。
	/*中序：先遍历左子树，然后再遍历根节点，最后遍历右子树，
	        故需要一个空间存放遍历左子树时经过的节点，且
			后遍历的节点先调用，故该空间可用栈来存放 
	*/ 
	BiTree p = NULL;
	int i = 0;
	SqStack S = {NULL,NULL,0};
	i = InitStack(S);  //构造一个栈
	i = Push(S,T);  //将根指针进栈
	while(StackEmpty(S) != OK){
		while(GetTop(S,p) == OK && p != NULL){
			//当可取栈顶元素时 
			i = Push(S,p->lchild);  //一路到最左
		}
		i = Pop(S,p);  //结束时会有一个空指针进栈，故需要将其退出
		if(StackEmpty(S) != OK){
			//访问结点，向右一步 
			i = Pop(S,p);
			if(visit(p->data) != 1){
				 return ERROR;
			} 
			i = Push(S,p->rchild);
		} 
	}
	return OK;
}

status InOrderTraverse2(BiTree T,status(*visit)(TElem e)){
	//同上，中序遍历2 
	int i = 0;
	SqStack S = {NULL,NULL,0};
	i = InitStack(S);
	BiTree p = T;
	while(p || StackEmpty(S) != OK){
		if(p){
			//根指针进栈，遍历左子树 
			i = Push(S,p);
			p = p->lchild;
		}else{
			//根指针退栈，访问根节点，遍历右子树
			i = Pop(S,p);
			if(visit(p->data) != 1){
				return ERROR;
			} 
			p = p->rchild;
		}
	} 
	return OK;
}
    
status LevelOrderTraverse(BiTree T,status(*visit)(TElem e)){
	//层序遍历，从上到下，从左到右
	/* 
	  树是肯定没发直接将一层的节点挨个遍历，它只能将一个树枝上
	  的节点遍历完后再去遍历其他节点（否则不容易检查节点是否被遍历） 
	  显而易见，这肯定需要另一个空间存储该树枝上该层下的节点
	  并且先放进去的节点是原节点下一层的节点所以最好先取出来
	  故该存储空间选用队列
	  继续分析下去， 当根节点进入又推出时，该其左右孩子都进入了，此时
	  需要判断一下其是否有左右孩子。 
	*/
	LQueue L = {NULL,NULL};
	int i = 0;
	BiTree e;
	i = InitQueue(L);//初始化队列
	i = EnQueue(L,T);//根节点入队列
	while(QueueEmpty(L) != OK){
		i = DeQueue(L,e);
		if(visit(e->data) != OK){
			return ERROR;
		}
		if(e->lchild != NULL){
			//如果有左孩子，则将左孩子入队列
			EnQueue(L,e->lchild); 
		}
		if(e->rchild != NULL){
			EnQueue(L,e->rchild);
		}
	}
	return OK;
}
       
status BiTreeDepth(BiTree T){
	//求二叉树深度,同样需要用到递归调用
	/*对该节点左右孩子节点调用该函数，
	  并进行比较 ，取节点深度更大的那个 
	*/
	if(T){
		int m = BiTreeDepth(T->rchild);//定义一个m为右孩子的深度
		int n = BiTreeDepth(T->lchild);//定义一个n为左孩子的深度
		int max = m>n?(m+1):(n+1);//求两者最大值，并返回最大值加一
		return max;  //max为最大值加一，因为返回到上一层深度加一 
	} else{
		return ERROR;
	}
}	
         
//栈函数
status InitStack(SqStack &S){
	//构造一个空栈。 
	S.base = (BiTree*)malloc(INIT_SIZE * sizeof(BiTree));
	S.top = S.base;
	S.stacksize = INIT_SIZE;  //初始为100 
	return OK; 
}

status Push(SqStack &S, BiTree T){
	//用于存储节点
	if((S.top - S.base) >= S.stacksize) {
		//栈满,追加空间 
		S.base = (BiTree*)realloc(S.base,(S.stacksize + CREMENT) * (sizeof(BiTree))); 
		S.top = S.base + S.stacksize;
		S.stacksize += CREMENT;
	}
	*(S.top) = T; //将数据存入栈
	S.top++;	
	return OK;
}

status StackEmpty(SqStack S){
	//对栈进行判空
	if(S.top == S.base){
		return OK;
	}else{
		return ERROR;
	}
} 

status Pop(SqStack &S,BiTree &e){
	//出栈
	e = *(S.top-1);	
	S.top--;
	return OK; 
}

status GetTop(SqStack S,BiTree &p){
	//取栈顶元素 
	if(S.top == S.base){
		return ERROR;
	}else{
		p = *(S.top-1);
		return OK;
	}
}
    

//队列函数
status InitQueue(LQueue &L){
	//初始化队列
	L.front = L.rear = (Queue)malloc(sizeof(QNode));
	L.front->next = NULL;
	return OK;
} 

status QueueEmpty(LQueue L){
	//判空
	if(L.front == L.rear){
		return OK;
	} else{
		return ERROR;
	}
}

status EnQueue(LQueue &L,BiTree T){
	//入队列
	Queue p;
	p = (Queue)malloc(sizeof(QNode));
	p->data = T;
	p->next = NULL;
	L.rear->next = p;
	L.rear = p;
	return OK;
}

status DeQueue(LQueue &L,BiTree &e){
	//出队列
	Queue p;
	p = L.front->next;
	e = p->data;
	L.front->next = p->next;
	if(L.rear == p){
		L.rear = L.front;
	} 
	free(p);
	return OK;
}
算法之二叉树各种遍历
落日小屋
03-07 20万+
树形结构是一类重要的非线性数据结构，其中以树和二叉树最为常用。 二叉树是每个结点最多有两个子树的有序树。通常子树的根被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用作二叉查找树和二叉堆或是二叉排序树。二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2的 i -1次方个结点；深度
1364：二叉树遍历(flist)
weixin_67264402的博客
04-25 1225
【题目描述】 树和二叉树基本上都有先序、中序、后序、按层遍历等遍历顺序，给定中序和其它一种遍历的序列就可以确定一棵二叉树的结构。 假定一棵二叉树一个结点用一个字符描述，现在给出中序和按层遍历的字符串，求该树的先序遍历字符串。 【输入】 两行，每行是由字母组成的字符串（一行的每个字符都是唯一的），分别表示二叉树的中序遍历和按层遍历的序列。 【输出】 一行，表示二叉树的先序序列。 【输入样例】 DBEAC ABCDE 【输出样例】 ABDEC 读入后，根据层序找出根节点，用
6-4 二叉树的遍历
missing_snoopy的博客
10-30 384
二叉树的4种遍历，前序遍历，中序遍历，后序遍历，层序遍历。
详解二叉树的遍历
supermouse的博客
02-16 1万+
概述 二叉树的遍历是一个很常见的问题。二叉树的遍历方式主要有：先序遍历、中序遍历、后序遍历、层次遍历。先序、中序、后序其实指的是父节点被访问的次序。若在遍历过程中，父节点先于它的子节点被访问，就是先序遍历；父节点被访问的次序位于左右孩子节点之间，就是中序遍历；访问完左右孩子节点之后再访问父节点，就是后序遍历。不论是先序遍历、中序遍历还是后序遍历，左右孩子节点的相对访问次序是不变的，总是先访问左孩子...
二叉树的非递归遍历
Ekertree的博客
11-07 232
本题要求用非递归的方法实现对给定二叉树的 3 种遍历。 函数接口定义： void InorderTraversal( BinTree BT ); void PreorderTraversal( BinTree BT ); void PostorderTraversal( BinTree BT ); 其中BinTree结构定义如下： typedef struct TNode *Position; typedef Position BinTree; struct TNode{ ElementType
数据结构实验之二叉树二：遍历二叉树
王小平
08-10 385
题目链接 Problem Description 已知二叉树的一个按先序遍历输入的字符序列，如abc,,de,g,,f,,, (其中,表示空结点)。请建立二叉树并按中序和后序的方式遍历该二叉树。 Input 连续输入多组数据，每组数据输入一个长度小于50个字符的字符串。 Output 每组输入数据对应输出2行： 第1行输出中序遍历序列； 第2行输出后序遍历序列。 Example I
非线性数据结构：二叉树的遍历算法详解
12-03
最后，讨论了二叉树遍历在查找元素、复制二叉树和层次遍历等方面的应用，并对其时间复杂度和空间复杂度进行了分析。 适合人群：具备一定编程基础，正在学习或从事数据结构相关工作的研发人员。 使用场景及目标：① ...
数据结构：二叉树层次遍历算法解析及C语言实现
最新发布
12-03
以二叉链表作为二叉树的存储结构，编写以下算法： （5）计算二叉树最大的宽度（二叉树的最大宽度是指二叉树所有层中结点个数的最大值）。 分析 • 求最大宽度可采用层次遍历的方法，记下各层结点数， • 每层遍历...
数据结构实验2.2：二叉树遍历的一些应用.doc
10-29
此外，实验还涉及了三种基本的二叉树遍历方法： - 先序遍历：先访问根节点，再遍历左子树，最后遍历右子树。先序遍历常用于创建二叉树，因为它可以按照输入顺序构建出与原始序列对应的二叉树。 - 中序遍历：先遍历...
数据结构与算法：二叉树层次遍历及其应用
12-03
使用场景及目标：本篇文章适合用于提高对数据结构的理解和对算法的应用能力，尤其是在处理涉及多层级关系的数据集时。学习并练习文章中提到的技术点有助于提升面试表现和技术解决问题的能力。 其他说明：阅读时应...
二叉树的遍历
E_N_T_J的博客
12-07 524
         二叉树的遍历问题是二叉树的基本核心问题，其他的所有问题基本都是在利用遍历来进行求解，遍历是访问所有的元素并打印或保存访问的元素，而其他问题也是访问所有元素，只不过有特殊的对访问元素的处理操作，因此基本所有问题都是遍历问题的改动。有时二叉树的遍历题目还需要结合集合类的工具，collection中的集合工具对数据进行操作。           二叉树的遍历常见的有先序、中序、后序、...
二叉树的层次遍历
L的博客
01-28 1594
本题依然是层序遍历，只不过在单层遍历的时候记录一下本层的头部节点，然后在遍历的时候让前一个节点指向本节点就可以了。需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点.关键点在于queue.size()在上一题基础上反转结果即可。
JAVA中的树(二叉树AND红黑树)
懿的博客
05-19 3105
JAVA中在HashMap中，在JDK1.8之后，就出现了红黑树，那么我们就得研究一下这个数据结构了，毕竟框架都是对底层进行的封装，那么我们 一起看一下吧。 二叉树 二叉树：二叉树是每个节点最多有2个子树的一种数据结构。 我们画图来了解一下吧，毕竟画图比较清晰。 二叉树的最高层就是根节点，下面又有很多的子节点，25是15的父节点，而15又是25的子节点，其实就是一个相互的关系， 而15和44又...
6-4 二叉树的非递归遍历 (25分)_二叉树与红黑树
weixin_39867662的博客
11-28 273
红黑树在工程中的使用，红黑树是平衡树的一种。1. 红黑树顺序的功能2. 快速查找的功能1.二叉树插入1. 如果比当前根节点大，就插到右子树2. 如果比当前根节点小，就插到左子树3. 再与根节点的子树去比较，决定插入到左子树，还是右子树。一直到左右子树为空的情况。注意：二叉树的插入，只能作为叶子节点。代码中的tmp指向的是node的父节点。下图的根节点是tmp指向的，node是指向根节点的子节点。/...
6.4二叉树的遍历-非递归
wangwei14309的专栏
10-22 599
6.4二叉树的遍历-非递归 （0）
数据结构-二叉树
雨后的空气
04-04 604
二叉树是树的特殊一种，具有如下特点：1、每个结点最多有两颗子树，结点的度最大为2。2、左子树和右子树是有顺序的，次序不能颠倒。3、即使某结点只有一个子树，也要区分左右子树。一、特殊的二叉树及特点 1、斜树所有的结点都只有左子树（左斜树），或者只有右子树（右斜树）。这就是斜树，应用较少2、满二叉树所有的分支结点都存在左子树和右子树，并且所有的叶子结点都在同一层上，这样就是满二叉树。就是完美圆满的意思...
6-4 二叉树的非递归遍历 (25分)_Python常用算法学习(5) 树二叉树（原理+代码）-最全总结
weixin_39901213的博客
11-23 375
1，树　　树是一种非常重要的非线性数据结构，直观的看，它是数据元素(在树中称为节点)按分支关系组织起来的结构，很像自然界中树那样。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到了广泛应用，如在编译源程序时，可用树表示源程序的语法结构。又如在数据库系统中，树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可以用树来描述。　　树(Tre...
二叉树
luyuncsd123的专栏
09-05 993
二叉树的遍历是指按照一定次序访问二叉树中的所有节点，且每个节点仅被访问一次的过程。是最基本的运算，是其他运算的基础。      二叉树有两种存储结构：顺序存储和链式存储     顺序存储：  （对完全二叉树来说，可以充分利用存储空间，但对于一般的二叉树，只有少数的存储单元被利用） [cpp] view plaincopyprint? typedef struct
二叉树遍历（前序、中序、后序、层次遍历、深度优先、广度优先）
热门推荐
My_Jobs的专栏
02-03 43万+
二叉树是一种非常重要的数据结构，很多其它数据结构都是基于二叉树的基础演变而来的。对于二叉树，有深度遍历和广度遍历，深度遍历有前序、中序以及后序三种遍历方法，广度遍历即我们平常所说的层次遍历。因为树的定义本身就是递归定义，因此采用递归的方法去实现树的三种遍历不仅容易理解而且代码很简洁，而对于广度遍历来说，需要其他数据结构的支撑，比如堆了。所以，对于一段代码来说，可读性有时候要比代码本身的效率要重要的
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值