KNN
相关概念及流程
概念
- 邻近算法,常见数据挖掘分类算法中最简单的方法之一。所谓K近邻,即K个距离最近的邻居,说的是每个样板都可以用它最近的K个邻居来代表。
类型
- 分类算法,基于实例的学习(instance-based learning)。 数据集实现已有分类和特征值,待收到新样本后直接进行处理,与急切学习(eager learning)相对应
特点
- 惰性学习(lazy learning:无训练阶段),数据集已经有了分类和特征值
- 待收到新样本直接进行处理。
算法思想
KNN是通过测量不同特征值之间的距离进行分类。
实现思路
- 如果一个样本在特征空间中的K个最近邻的样本中大多属于某一个类别,则该样本也划分为这个类别(已有多数样本最佳类别投票表决新样本分类)
注意事项
- KNN算法中,选择的邻居都是一件进行正确分类的对象,该方法在定类决策上只依据最近邻的一个或几个样本类别来决定待分样本所属的类别。
图示

需要确定绿点属于哪个颜色(红色或蓝色),通过计算红色和蓝色点距离目标点的距离,要做的就是选出距离目标点距离最近的k个点,看这个k个点大多数的颜色是什么颜色。
当k=3时,我们可以看到距离最近是三个,分布是红色、红色、蓝色,因此得到目标点为红色。
步骤
- 计算目标点(测试数据)与各个训练数据(已知样本类别)之间的距离
- 按照距离目标点的距离进行递增排序
- 选取距离最小的k个点(可以对各个样本的距离集合进行排序)
- 选取距离最小的k个点
- 确定前k个点所在类别的出现频率(前k个点各个类别出现次数)
- 将k个点中出现频率最高的类别作为目标点(测试数据)的预测分类
关于K的取值
K的意义
临近数 -- 预测目标时去几个距离最近的邻近的的来预测,非常重要。
k值选取注意事项
- k值选取过小,一旦有噪音成分存在将会对预测产生较大影响.如k=1,一旦最近的一个点是噪声,那么就会出现偏差。k值得减小就意味整体模型变得复杂,易过拟合。
- k值选取过大,相当于用较大邻域中的训练实例进行预测,学习的近似误差会增大。这是与输入的目标点较远实例也会对预测起作用,使预测发生错误。同时意味整体模型变得简单。
- k值如果k==N(为数据所有样本分类下最多的点),去实例中所某分类下最多的点,对预测无意义。
- k值尽量取奇数,以保证在计算结果最后会产生一个较多的类别,如果取偶数可能会产生相等的情况,不利于进行预测。
k值取法
- 一般从k=1开始,使用检验集估计分类器的误差率。重复该过程,每次递增1,允许增加一个近邻,选取产生误差率最小的k值。
- 一般k取值不易超过20,上限是N的开方,N为所有样本分类最多的点的总数。
- 随着数据集的增大,k值也要增大。
关于距离输入的目标点的距离选取
距离度量方法
- 距离即平面两点的直线距离
- 度量方法
- 欧几里得距离(欧氏距离):计算坐标上两点的实际距离
- 计算公式(两个点或元组P1=(x1,y1),P2=(x2,y2))
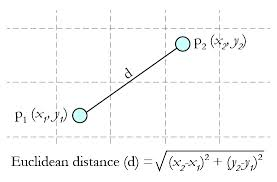
- 多个维度(是多个维度各自求方差后再同意开方)

- 计算公式(两个点或元组P1=(x1,y1),P2=(x2,y2))
- 欧几里得距离(欧氏距离):计算坐标上两点的实际距离
总结
- KNN算法是最简单最有效的分类算法,简单且容易实现。当训练集很多时,需要大量存储空间,而且需要计算待测样本与训练集中所有样本距离。所以非常耗时。
- KNN对随机分布的数据集分类效果较差;对类内间距小,类间间距大的数据集分类效果,而且对于边界不规则的数据集效果好于线性分类器
- KNN对于样本分布不均衡的分类效果不好,需改进。改进方法对k个近邻数据赋予权重,距离越近,权重越大。
- KNN比较耗时,时间复杂度为o(n),一般使用样本数据较少。当数据量大时,可以将数据以树的形式呈现,能提高速度,常用的有kd-tree,ball-tree.
python实现
#-*- coding:utf-8 -*-
#Author:Jerry
import csv
import random
import math
import operator
class KNNClassfier:
def __init__(self, k, filename):
self.k = k
self.filename = filename
def load_dataset(self, filename, spilt, traing_data, test_data):
"""
从csv中加载数据集
:param filename:
:param spilt: 数据拆分的比例
:param traing_data: 已存在的数据集
:param test_data:输入的待预测数据
:return:
"""
csv_file=open(filename,mode='r')
read_csv = csv.reader(csv_file)
# 将csv文件转换为集合
dataset = list(read_csv)
for x in range(len(dataset)-1):
for y in range(4):
dataset[x][y] = float(dataset[x],[y])
# 将数据集随机拆分
if random.random() < spilt:
traing_data.append(dataset[x])
else:
test_data.append(dataset[x])
def enclidean_distance(self, instance1, instance2, length):
"""
计算已有数据每个样本与待预测目标点的距离
:param instance1: 待预测目标点
:param instance2: 已知数据集的每个样板
:param length: 每个样本包含特征数量
:return:
"""
distance = 0
# 根据多维度欧式距离计算公式进行计算
for x in range(length):
# sum = (a1-a2)^2 + (b1-b2)^2 + (c1-c2)^2 +...+ (z1-z2)^2
distance += math.pow(instance1[x]-instance2[x],2)
# 对sum开根号后返回
return math.sqrt(distance)
def get_nearest_k_neighbors(self, traing_data, test_instnace, k):
"""
计算待测目标点与已有数据集每个样本的距离
:param traing_data: 已有数据集
:param test_instnace: 待测目标点样本
:param k: k 近邻个数
:return:
"""
# 存放已有数据集与待测目标点的距离
distances = list()
# 已有数据集中每个样本的特征数量,不包含y标签(分类结构)
length = len(test_instnace) - 1
for x in range(len(traing_data)):
# 获取待测目标点与已有数据集的每个样本的距离
dist = self.enclidean_distance(test_instnace, traing_data[x], length)
# 保存已有数据集每个样本和与待测目标距离的对应关系
distances.append((traing_data[x], dist))
# 对保持待测目标点与已有数据集样本的距离的集合进行逆序(降序排列)
# 根据距离进行排序
distances.sort(key=operator.getitem(1))
# 获取k个距离最近的样本的分类的类别集合
k_neighbors = list()
for x in range(k):
# 将k个距离最近的已有数据集样本作为k个近邻
k_neighbors.append(distances[x][0])
return k_neighbors
def predict(self,k_neighbors):
"""
通过获取k个近邻的多数分类的类别数量
将类别最多的类别作为待测目标的类别(k近邻的多数类别作为待测目标点的类别)
:param k_neighbors:
:return:
"""
class_votes = dict()
for x in range(k_neighbors):
# 获取k个近邻样本数据中的最后一个字段(类别,y_label)
# k_neighbors为二位数组,获取每个元素数组的最后一个元素
y_label = k_neighbors[x][-1]
# 进行k个近邻的类别统计
if y_label in class_votes:
class_votes[y_label] += 1
else:
class_votes[y_label] = 1
# 对 k个近邻的类别进行降序排列,获取类别出现频率最多的一个类别
# a = {"a": 1, "b": 2, "c": 5, "d": 6}
# sorted(a.items(), key=lambda kv: kv[1], reverse=True)
# [('d', 6), ('c', 5), ('b', 2), ('a', 1)]
sorted_class_votes = sorted(class_votes.items(),key=lambda kv:kv[1],reverse=True)
# 返回类别频率最后的一个
return sorted_class_votes[0][0]
@staticmethod
def accuracy(test_data, predictions):
"""
计算测试集的预测的准确率
:param test_data: 测试数据集
:param predictions: 测试集类别预测结果集合
:return:
"""
correct = 0
for x in range(len(test_data)):
# 如果预测的结果跟待测的数据集类别相同,则+1
if test_data[x][-1] == predictions[x]:
correct += 1
return (correct/float(len(test_data)))*1000
if __name__ == '__main__':
# train_data
train_data = list()
# 测试集
test_data = list()
# 数据拆分比例(训练集与测试机的比例)
split = 0.67
k = 3
csv_path = "/home/jerry/iris.csv"
knn = KNNClassfier(k=k, filename=csv_path)
knn.load_dataset(knn.filename, split, train_data, test_data)
# 存放测试集每个样本预测类别
predictions = list()
# 获取测试数据集每个样本的k个近邻
for x in range(len(test_data)):
neighbors = knn.get_nearest_k_neighbors(train_data, test_data[x], k)
# 获取测试集每个样本的预测标签
result = knn.predict(neighbors)
predictions.append(result)
print("predicted = "+repr(result)+', actual = '+repr(test_data[x][-1]))
# 计算准确率
accuray = knn.accuracy(test_data,predictions)
print("Accuray = "+repr(accuray)+"%")
sklearn实现
#-*- coding:utf-8 -*-
#Author:Jerry
from sklearn import neighbors
from sklearn import datasets
from sklearn.mode_selection import train_test_split #引入数据集拆分的模块
#加载数据集
iris = datasets.load_iris()
#数据拆分比例及随机种子
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
#构建模型
knn = neighbors.KNeighborsClassifier()
#计算训练集与测试集的距离
knn.fit(X_train, X_test)
#预测测试集类别
predictedLabel = knn.predict([[0.1, 0.2, 0.3, 0.4]])
print ("predictedLabel is :" + predictedLabel)

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








