左 . （进阶）算法---树 专题

二叉树的三种遍历方式（递归/非递归）

时间复杂度为O(n)

额外空间复杂度均为O(h)   h为树的高度

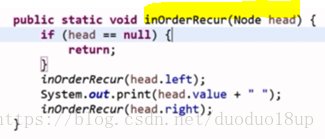
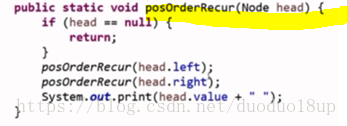
递归版：

非递归版：

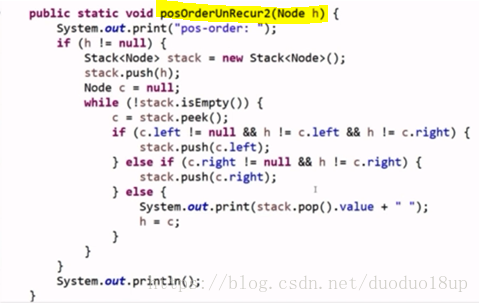
后序遍历的非递归（用2个栈）：

后序遍历的非递归（用1个栈）：

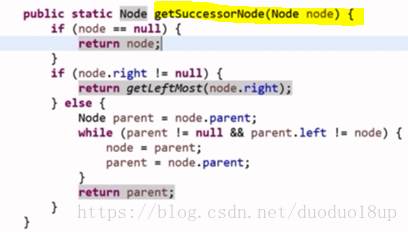
在二叉树中找到一个节点的后继节点：

思路： 中序遍历  左根右

主要考虑两种情况（有无右孩子节点）

如果该节点    有右孩子节点 ，  则是右孩子节点中的最左孩子节点。

                     没有右孩子节点---则找父节点----直到找到是其父节点左孩子的节点

存在特殊情况：  如果node是整棵二叉树的最后一个节点---则在逐步往上走父节点的时候----可能会走到根节点--- 根节点的父节点为null  (有判断父节点是否为空）----所以最后一个节点的后继节点为null

如果题目改为求 一个节点的前驱结点：

考虑 是否有 左孩子节点 ----  如果 有左孩子节点 ---则前驱结点就是左孩子节点最右节点

                                             如果没有左孩子节点---则往上追溯--只要父节点是当前节点的右孩子即可

二叉树的序列化和反序列化：

按照先序遍历的思路（递归式）

序列化：

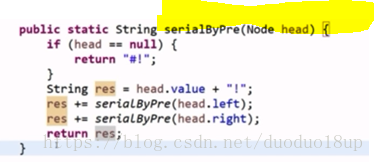
反序列化：

按照层序遍历的思路（非递归式）

序列化：

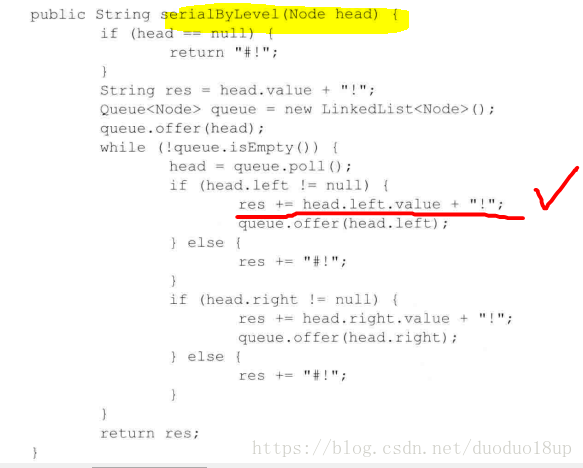
反序列化：

 

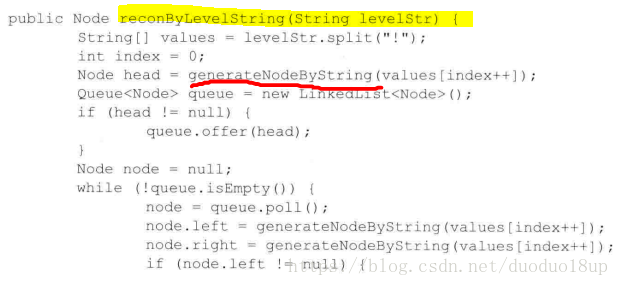
判断一棵二叉树是否是平衡二叉树？

解决这个问题：我们需要充分利用递归的特点

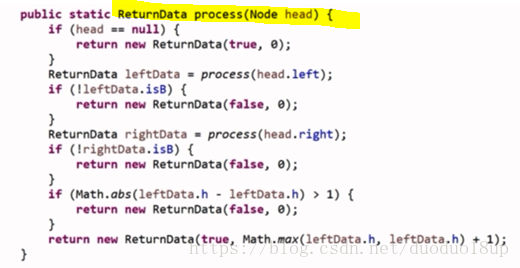
判断一个节点是否平衡   需要获取的信息有： 左平    右平   左高  右高    

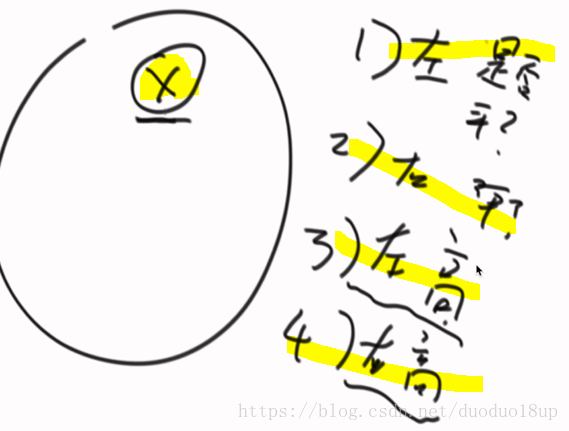
定义  需要返回的内容信息（是否平衡+ 高度）：

开始递归函数的逻辑：

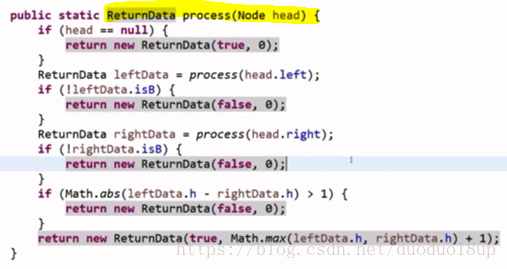
主函数逻辑：

判断一棵树是否是搜索二叉树，判断一棵树是否为完全二叉树？

思路：

搜索二叉树

是  :  根节点的左子树值<根节点的值    右子树的值>根节点的值

所以想到  中序遍历的结果如果是 升序的 则证明是一个二叉搜索树

在非递归中序遍历中  我们记录上一个弹出结果值和当前弹出结果值  比较大小  然后加一个return值

黄色区域改为

  if(pre< head.val)
      pre=head.val;
  else 
       return false;


XXXXXX
return true;

完全二叉树：

考虑两种逻辑：

1    当前节点有右孩子 没有左孩子  直接返回false

2    当前节点 有左孩子 但是没有右孩子   或者 左右孩子都没有    则 判断后面遇到的节点是否都为叶节点 

按层序遍历的思路 ：

其中左右判断阶段代码等同于：

已知一棵完全二叉树 ，求其节点个数：

思路：

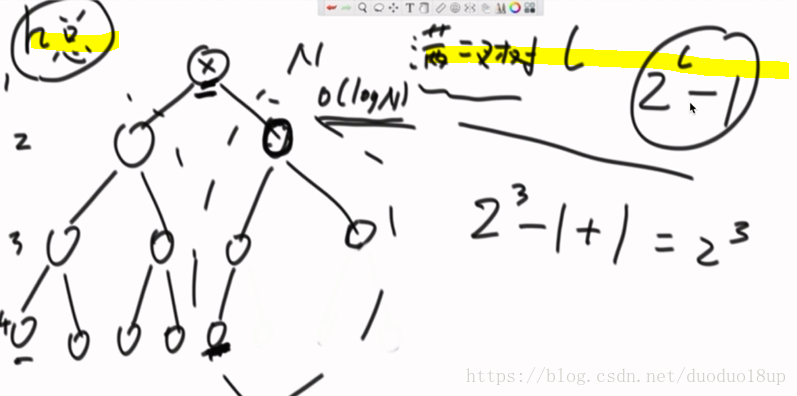
满二叉树个数：        深度L    总个数为 2L-1  （L为指数）

当前节点标记为X：  一直到左孩子  统计深度    

                                然后找到X的右孩子的最左节点---    情况1 ：如果最左节点已经到了最后一层  （见上图）

                                                                                                    则根节点的左节点数目确定2（L-1)-1 +1 =2(L-1)

                                                                                                    之后再确定 右孩子的具体个数  ------求和

                                                                                       情况2 ：最左节点没有到最后一层 （见下图）

                                                                                                    此时右子树是满的 +再确定左边个数--->和 为两部分加起来

      

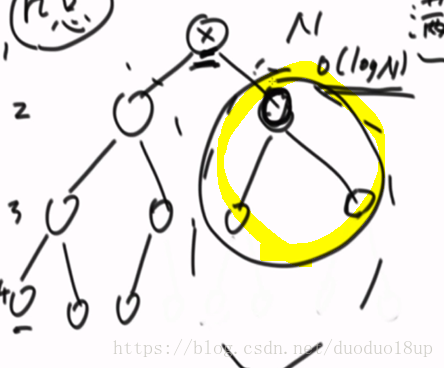
总的思路：

bs(以node 为根节点 在level层  h为总的深度（固定值）的完全二叉树的节点个数

最左节点深度到h则计算左边完全二叉树节点个数+递归右边求节点总个数

没到h 则右边完全二叉树节点个数固定  +递归左边求节点总个数

分析时间复杂度：

进阶篇：

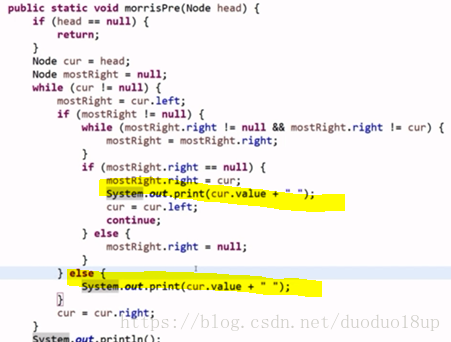
1 遍历方法的优化（Morris遍历）：

时间复杂度O(n) 空间复杂度为O(1)的二叉树遍历：

思路：

代码： 一一对应上述解说

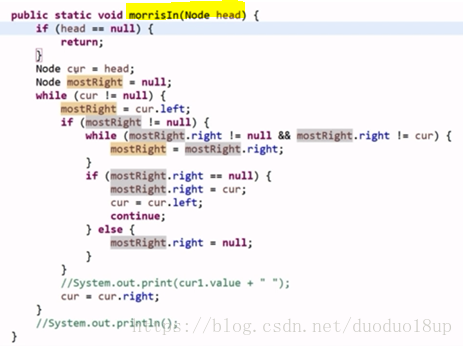
如何从基础理解：

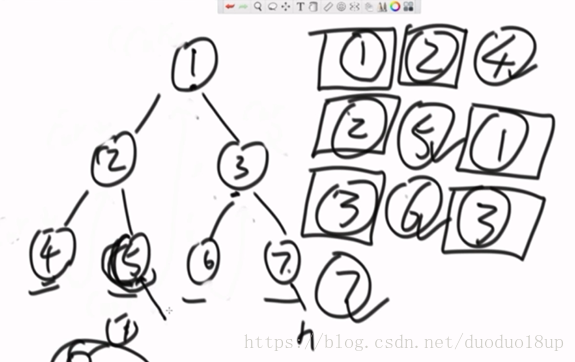
1.  还原到最初的遍历递归过程---

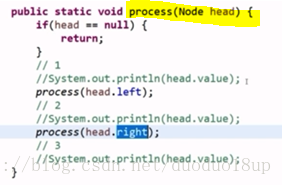
2. 理解：

先是head---head.left----head---head.right--head   只要节点不空则3次来到此节点

而Morris遍历 仿照此过程：     只是head.left时候  到达此节点2次    没有head.left时 只是到达一次

根据当前节点的左子树的最右节点是否指向当前节点  来判断是第几次指向

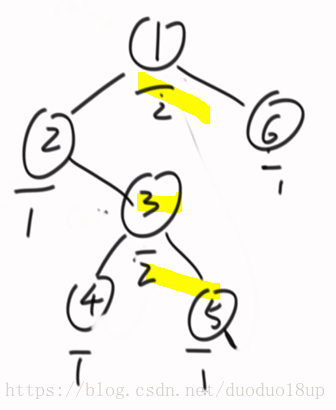
3 .对于那三种遍历方式  每一种的差别其实在于从哪次经过点时进行打印

    其实 最基础的均是递归  只是打印的时间点不同

4  想要改成先序遍历的方式  则只要在第一次经过节点的时候进行打印即可

     1） 当前节点没有左子树的时候 则不分中和左（相当于合并在一起）----打印之后---直接到右子树

     2）当前节点有左子树，则找到左子树的最右子树，此时打印即可

5  改成中序遍历的方式：

     左中右

     只要在往右边之前进行打印即可

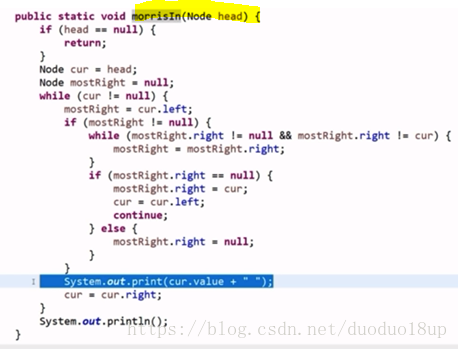
6  后序遍历：

只关注能够来到自己2次的节点 

打印时机是第二次来到，刚好将cur2.right重新调整回null的时候，逆序打印左子树的右边界 ，以及 最后在退出之前单独打印整棵树的右边界

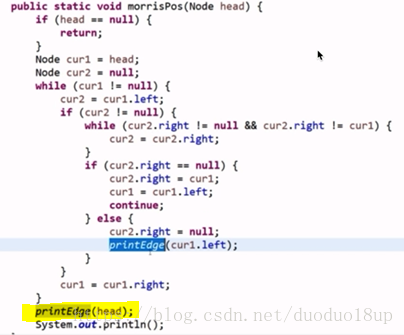
注意： 如何能够打印右边界

利用类似于链表reverse的功能

7 分析时间复杂度：O（N)

    右边界只是经过有限次

2 搜索二叉树

A.  常规的hashmap   里面的key-value  key 没有顺序

而TreeMap  中的key-value  key按照某种顺序（其实就是搜索二叉树）  底层红黑树（具有一定平衡性的搜索二叉树）

好处： 将key按照一定顺序组织之后 就能实现更多功能（e.g.查找某一个支对应节点是哪个位置）

B. 在实际工程中 ，如果单纯按照顺序插入删除搜索二叉树  那么树的形状可能和输入数字顺序有关

e.g.   1 2 3 4 5

我们必须对此作出一些调整：

引申为一些变体：

1 )  AVL树：（平衡性最严苛的一种树结构）

            要求：任何一个节点的左子树和右子树高度差不超过1 ，即使输入顺序不符合要求，但能够根据旋转等调节方式使其变平衡。

             优点：调整的代价依然是O(logn)

             缺点：可能调整的频率比较高

2）红黑树：

              要求：1. 每个节点都有颜色  头和叶节点必然为黑 相邻节点颜色不能都是红

                         2. 任何一条链黑色相差不能超过1

              暗含：每一条链都不能超过最短链的两倍（极端情况：一个使劲塞红 一个全是黑）

                        暗含了高度差最大不能超过两倍（也是一种平衡性的体现）

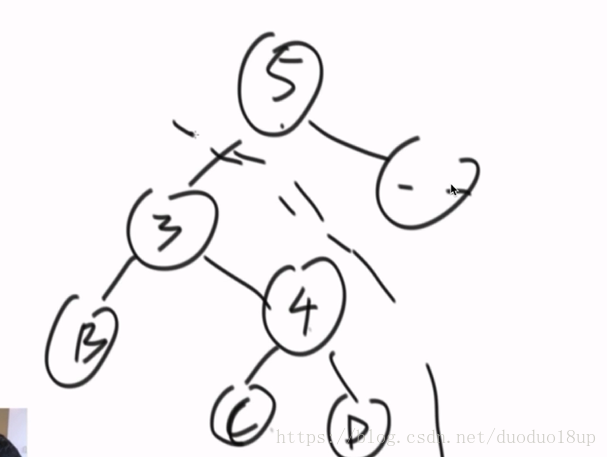
3）SB树： 如图所示

                  X是父节点

                  Y和Z是兄弟节点

                  Y是Y1.Y2的叔叔节点   同理Z

                    要求：作为叔叔节点 整棵树上的节点不能比任何一个子侄节点的节点树要少

                 e.g. Y的整棵树节点数不能比z1的整棵树的节点数要少。

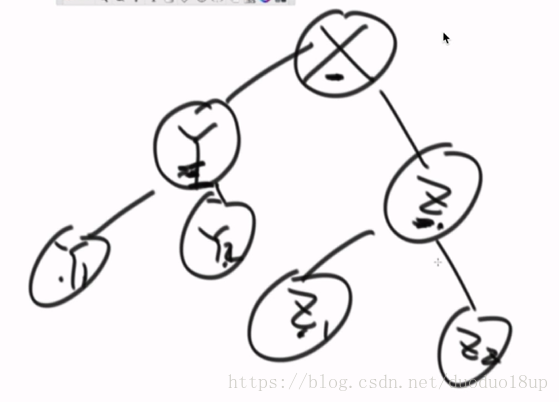
平衡性的要求 的目的：  为了实际中的调整方便（尽量左右达到一定的平衡性）

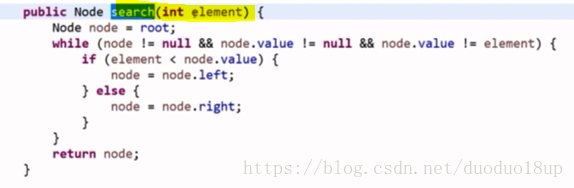
C  代码实现（增删查）：

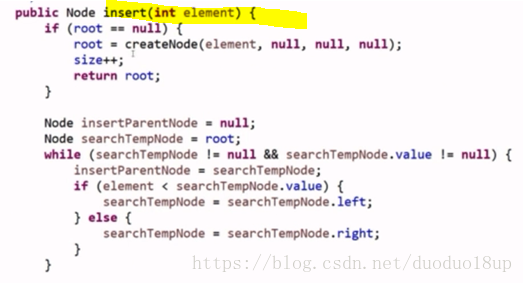
删除的逻辑：

1  如果要删除节点没有左节点/右节点   则直接存在的那方节点提上

2  如果双全  则选择后继节点（该节点左子树的最右节点代替 其下的移交即可）

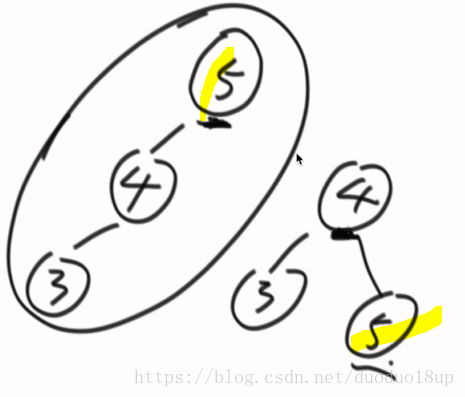
D . 对于所有这些变体的调整都是：左旋和右旋基础动作的组合

e.g.右旋  ：原来的头节点变成了新头节点的右节点

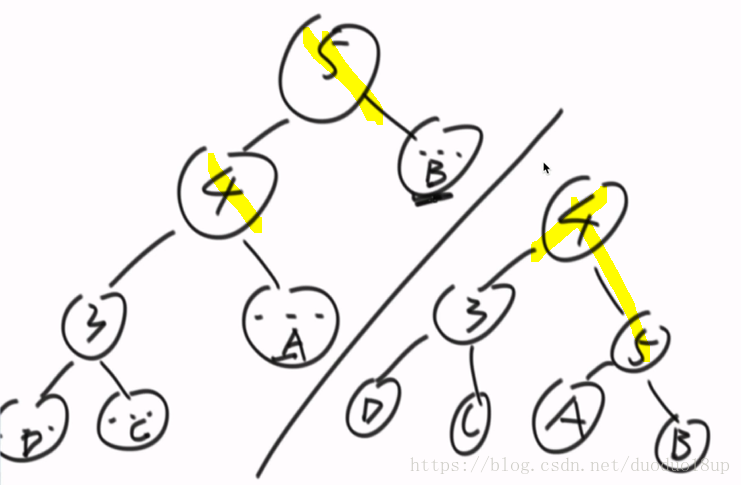
e.g.  左旋： 原来的头节点变成新头节点的左孩子

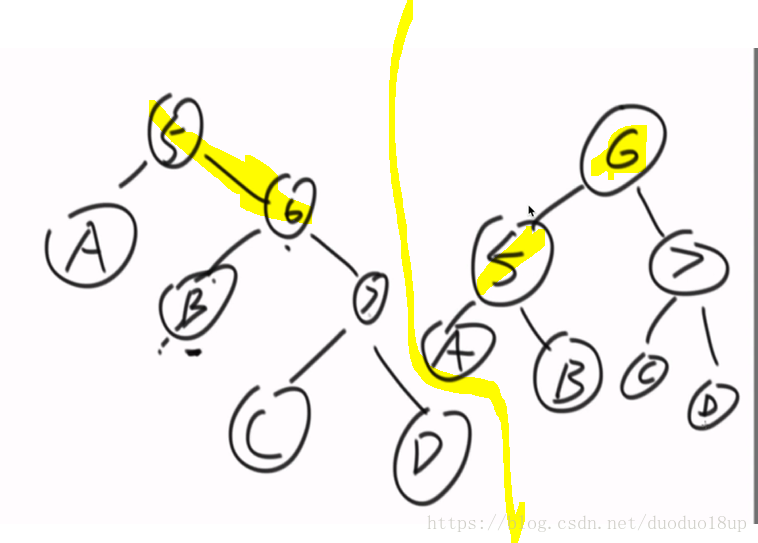
E  如何发现不平衡 需要进行修改~

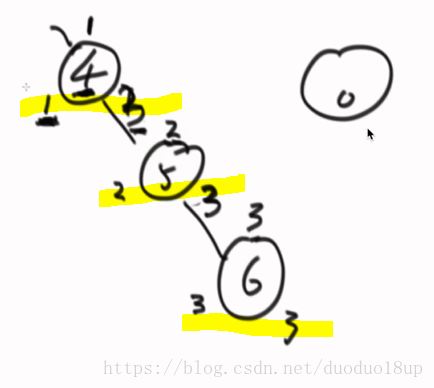
  每个节点会记录左右高度  只要插入一个节点 就会往上追溯  使高度+1

刚开始只有节点4   左右记录均为1 1

后插入5 后    5左右为2 2  往上追溯   到4的记录+1

直到后来发现左右差距不符合要求时需要进行相应的操作

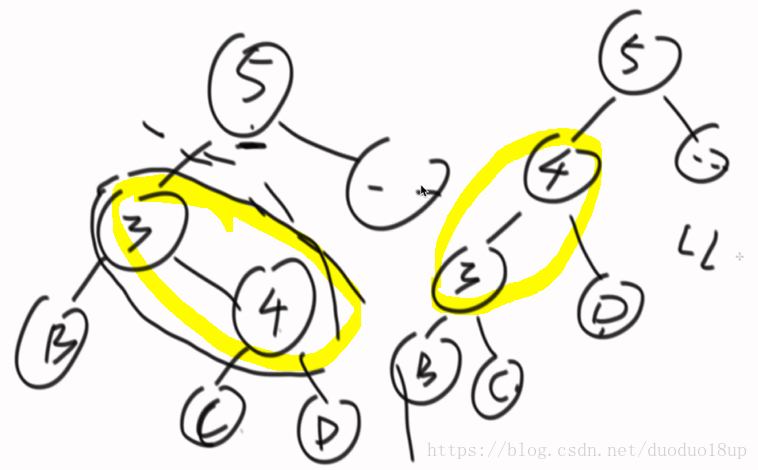
F。调整的组合有4种：

         LL   

         LR

         RR

         RL

  以AVL为例：

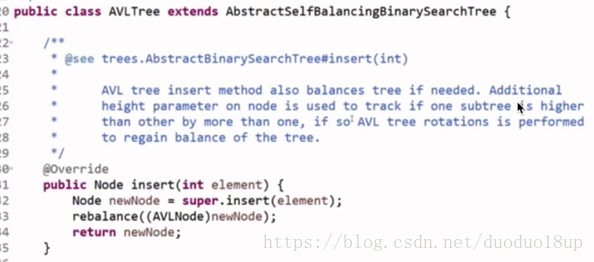
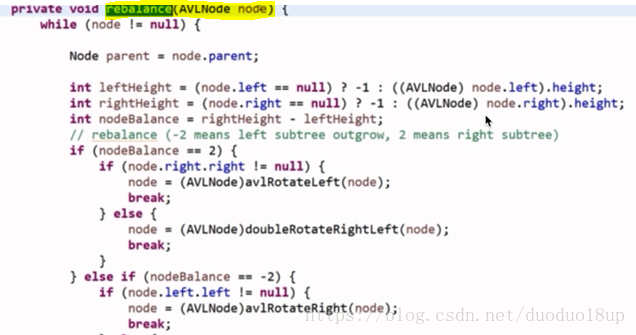
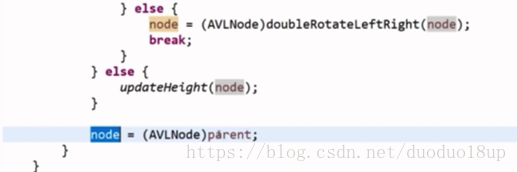
G .  LL：只有右旋操作 同RR  单一动作

LR： 先进行左旋--LL---再进行右旋  同理RL

3  搜索平衡二叉树的使用：

不要求会创建，要求会使用~

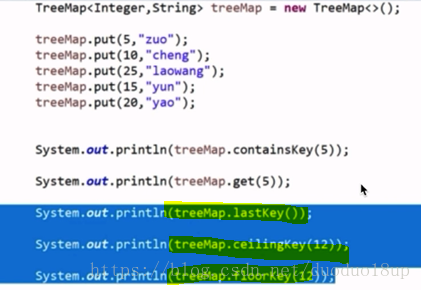
TreeMap底层结构是红黑树----插入元素按照一定顺序进行排序--每次修改只要时间复杂度为O(logn)

treeMap.lastKey()---最右端的值（就是最大值）  此时为25

treeMap.ceilingKey(num)---离num最近刚比num大的数字

treeMap.floorkey(num)----刚比num小的数字

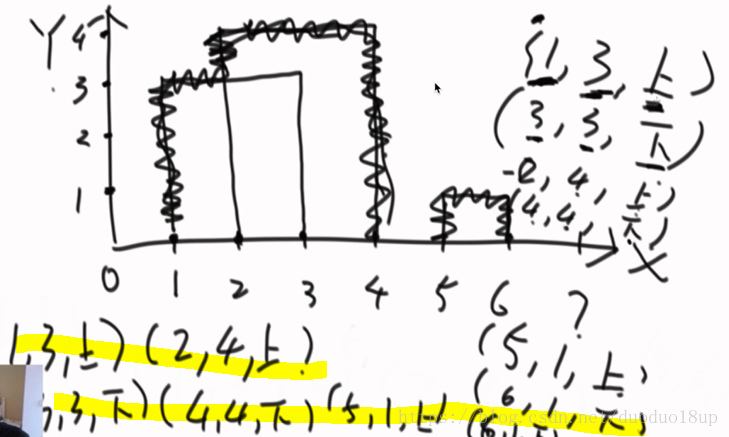
3.1  大楼轮廓线问题：

理解题意：

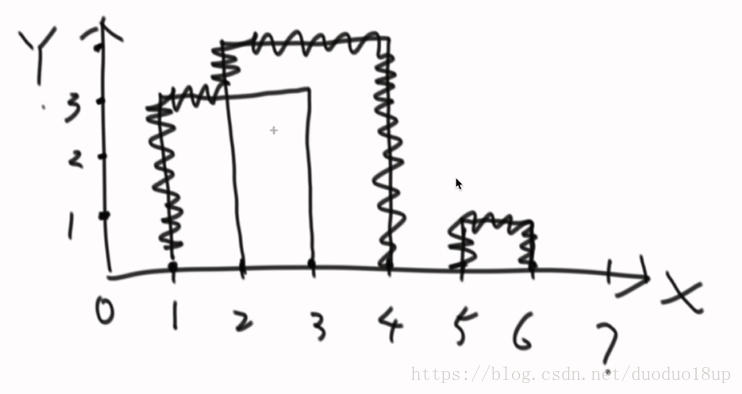
思路：

将原有的{1,3,3}---拆成两个   {1,3,top},   {3,3,down}  意思是： 在1处上去了高度为3

举例说明：

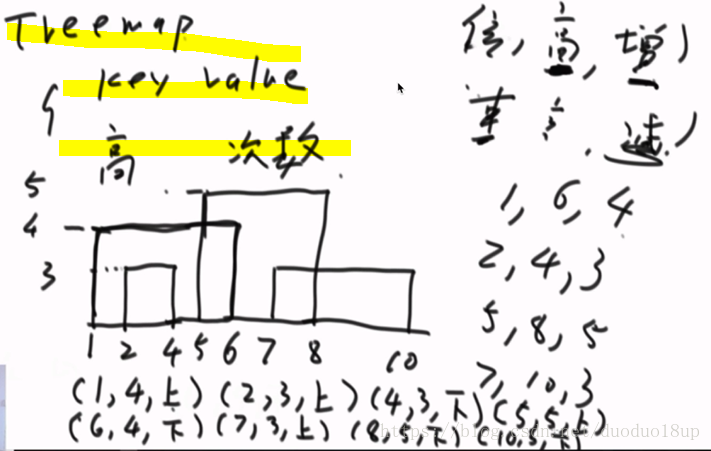
举例分析流程：

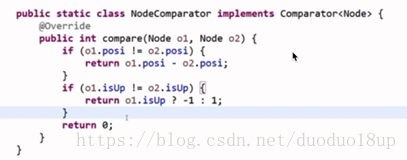
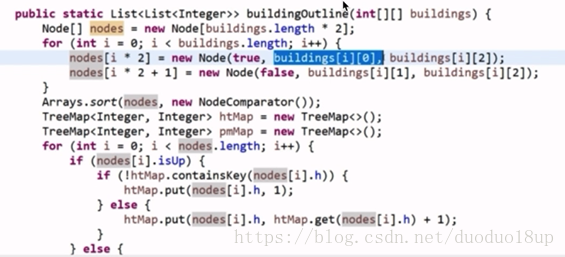
1  将原有数组分为两个部分--原有格式(o,d,h)---变成（o,h,up)+ (d,h,down)

2  建立一个TreeMap htMap 用来记录 key=高度  value=高度出现的次数

     注意： 当数组元素为(o,h,up)时 htMap记录并将次数+1   而当元素为(d,h,down)时 htMap记录次数-1

3  建立一个TreeMap pmMap 用来记录key=pos  value=pos对应的最大高度  

    注意： 主要就是根据htMap的记录来判断  -----若htMap为空 证明所有元素均已经走完 则高度最终降为0

               -----若htMap不为空 则每次获取lastKey 即为最大高度

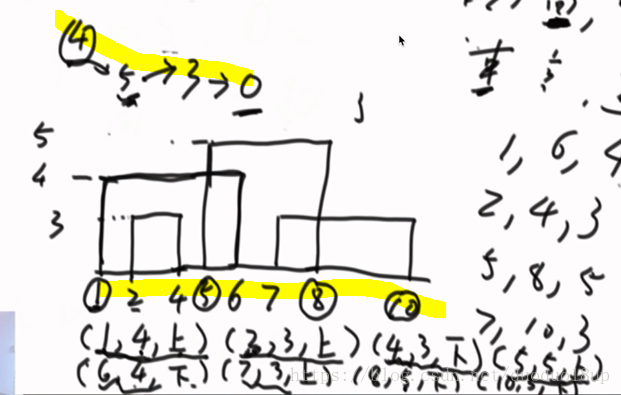
pmMap的记录实例：

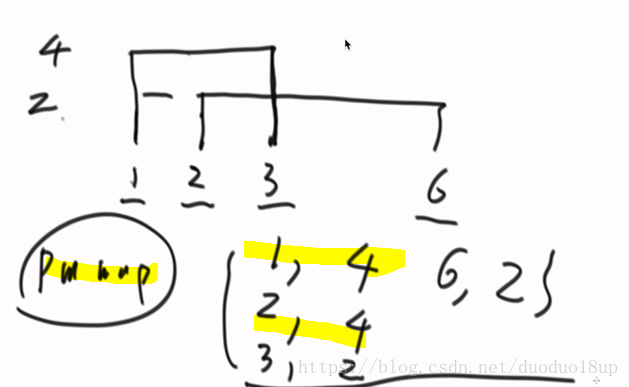
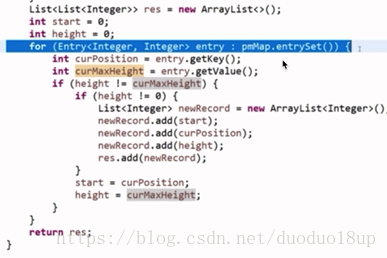
重建轮廓线的流程：

根据最大高度变化的位置进行切点  需要判断原高度与现在最大高度是否一样

若不一样 证明开始出现轮廓线    且必须注意之前的高度不为0时才有格式为(原开始位置， 当前高度变化位置， 原高度）

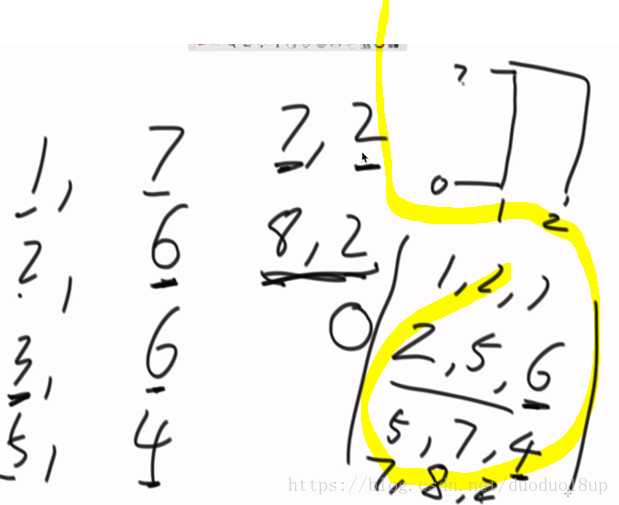
代码实现：

最核心逻辑： 跟踪每个位置最大高度的变化，生成所有轮廓线~

根据每个map记录值的大小 判断是否是上升或者下降 阶段--画出轮廓线

htMap:  key为高度  value为出现此种高度的次数

pmMap； 当前位置（key)的最大高度(value)

             

     

       

3.2 累加和给定的最长子数组问题：

题意： 给定一个无序数组  有0 正 负数 再给定一个整数aim

           求累加和为aim 值的最长子数组

举例：

思路：

超级巧妙（这种连续子数组问题  均可以考虑从0开始累加至 sum-aim的范围  则剩下的部分即为满足条件的最长子数组）

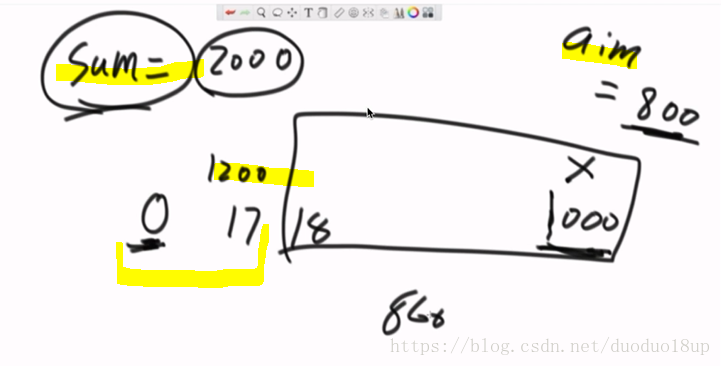
举例说明：

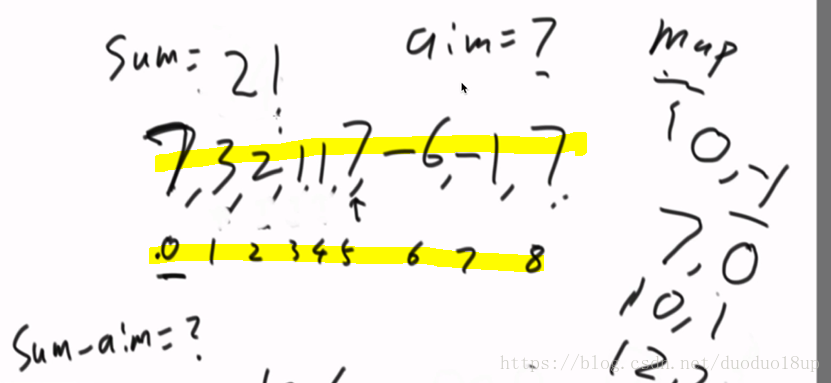
 数组 7 3 2 1 1 7 -6 -1 7

其中 sum=0;  aim=7; map{0,-1}{...}

 1   sum=7   aim=7   map{0,-1} {7,0}

 2   sum=10  aim=7  以3结尾构不成需要结构   因为0位置为7

-----一直到sum=14  到i=4位置时  此时aim=7  从0-0  刚好为sum-aim =7 所以最长子数组为1-4 位置上元素构成的子数组

------ 一直走到数组完毕

map 记录第一次出现从0-某一位置的和： { 0,-1}  {7，0} {10，1}  {12，2} {13，3}  {14，4} {21，5} {15，6}

在sum=14  i=7 时   最长子数组 1-7位置   长度为7  更新最长子数组   但是map不进行更新 

在sum=21    i=8时  最长子数组4-8   长度为4   不更新最长子数组

注意：初始map一定得有{0,-1}这条记录  因为我们每次都是从下一位置到当前 位置   所以不加就会错过0 开始的多种可能。

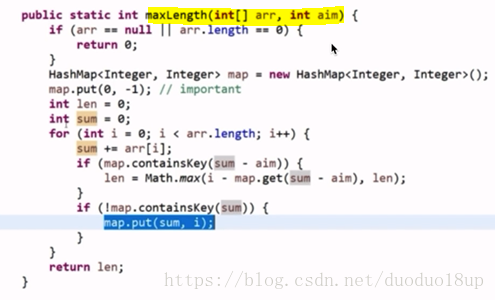
代码实现：

3.3 变体：求奇数和偶数个数相等的最长子数组

思路： 奇数1  偶数-1  求累加和为0的中最长子数组即可

再变体：  一个数组中 只含有0 和1   求含有0和1 个数相等的最长子数组  

                 ----解法：1 仍然为1  0为-1  求累加和为0 的最长子数组

再变体：  一个数组中 0 12   1 和2 数目相等的子数组    2-->-1   依然求累加和为0 的最长子数组

3.4 异或和为0的子数组最多 问题（not resolve)：

题意：

一个数组可以有多种切分方式  如何切分成许多不相容子数组  使得出现异或和为0 的子数组个数最多？

举例说明：

需要知道：

异或运算  满足交换律和结合律

0和任何数异或都是0

解题思路：

1  0----i  0--i+1 --------0--n-1即为结果

2   在0--i中 ：有两种可能：  1) 包含i的最后部分异或和不为0    2).....为0

                1）和0---i-1 上切分数目一样（类似于dp)

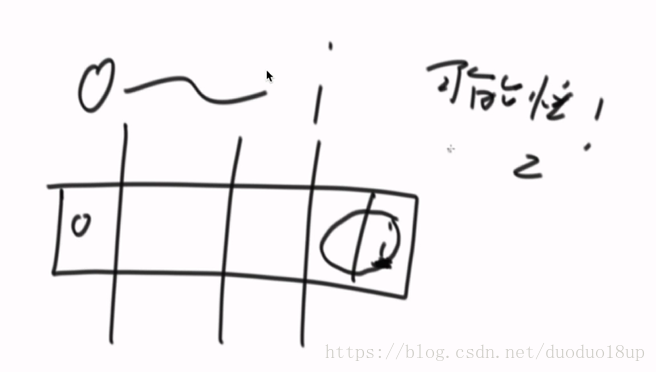
     2） 假设最后一个最优划分 为0 的部分是从k到i  则中间一定不存在更优的划分  

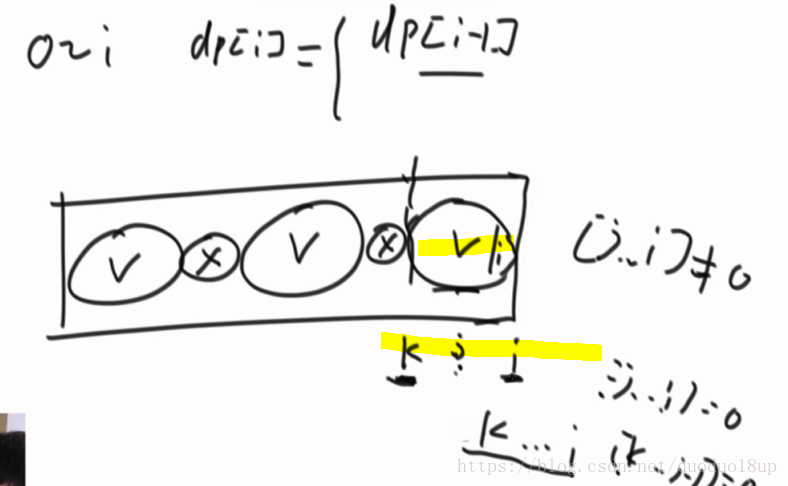
则综合上述可以推导出 式子：

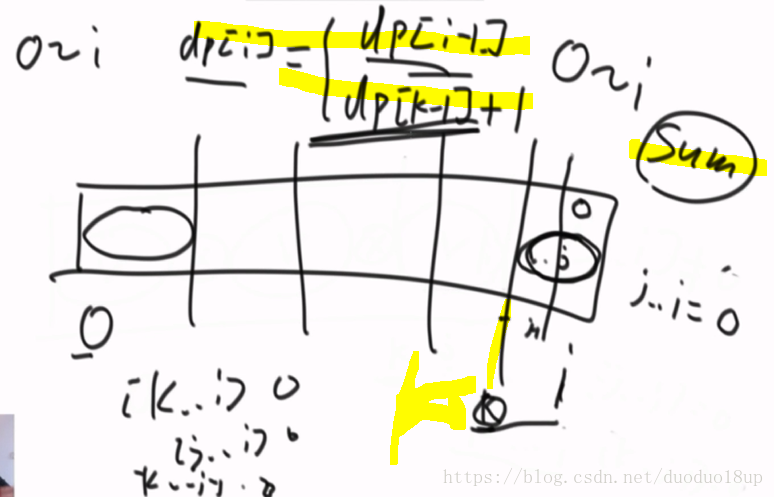
则问题转换为  k最晚出现的位置

代码实现：

注意  ：最后map.put(xor,i)   因为要求最晚出现的 ，所以需要不断的更新map 。

4 最大搜索二叉树的大小：

思路分析（有3种可能性）：

1  头节点的左子树 中含有最大搜索二叉树

2  头节点的右子树 。。。

3  头节点左子树和右子树均为搜索二叉树  ，且符合以头节点的规则  则整棵树就是最大搜索二叉树。

e.g.1

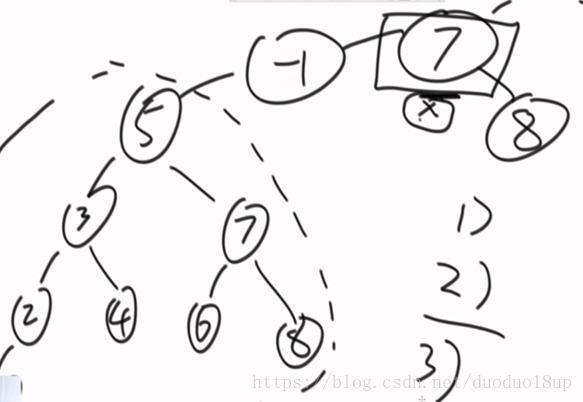
思路逻辑：

就是分别获得左右子树的相关信息----再确定头节点是否参与-判断第3种情况~

使用递归的思路---

需要拿到 的信息是:  

1 .左子树上最大搜索二叉树的大小

2. 右子树上最大搜索二叉树的大小

3 .左最搜的头部是否是头节点的左孩子（相当于判断左子树是否整个都是）

4 .右。。。。。。同3

5 左树上的max

6 右树上的min

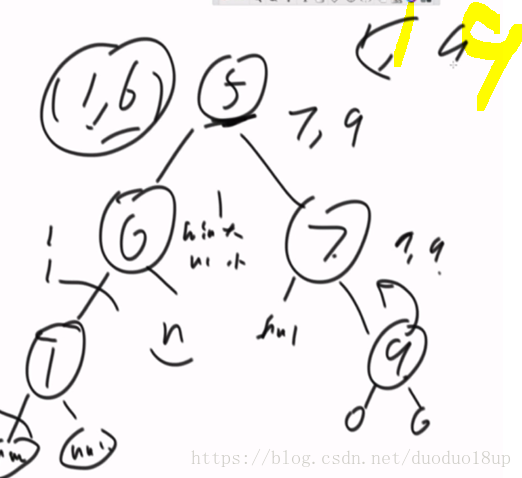
举例：不满足3

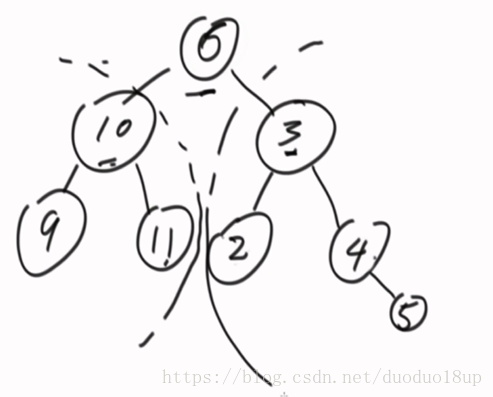
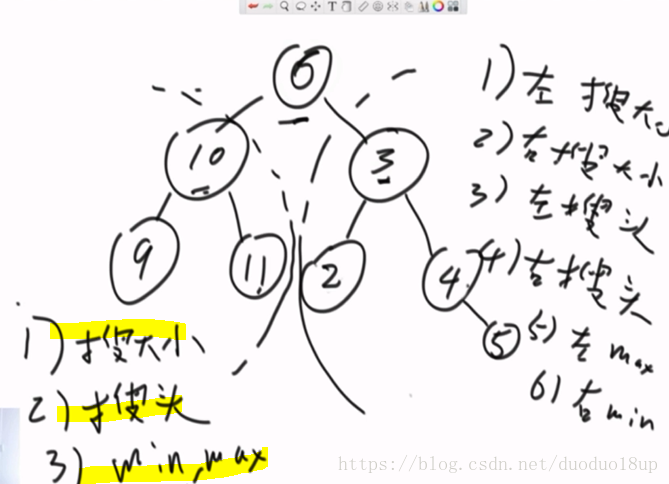
精简思路：

统一结构体~

简单例子：

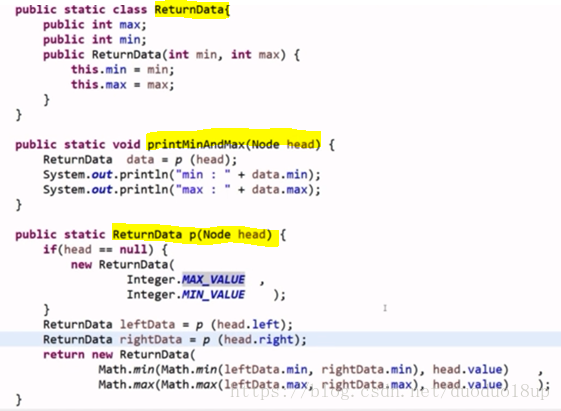
整棵树上求最大值和最小值

注意：head为空时：用系统最大值代替min 用系统最小值代替max

对应：

原题代码书写：

中间是可能性3  后面两个p1 p2为可能性1 和2

 

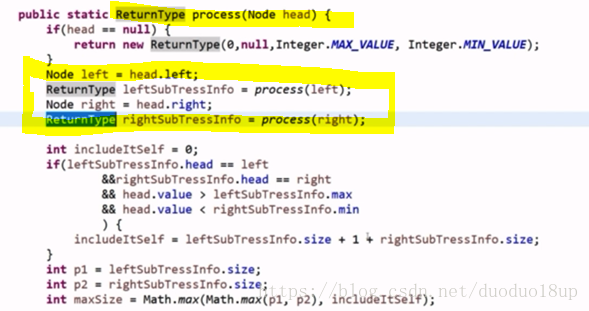
4.1  变体：二叉树上最远距离

分析题意 存在3 种可能性：

1 在头节点的左子树上最大深度

2 在头节点的右子树上

3 经过头节点  左子树上最大深度  右子树上的最大深度

代码实现：

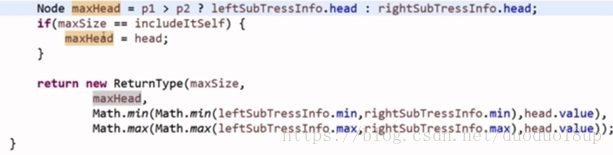
对应3种情况-----递归--黑盒解决---最终返回

  主函数：

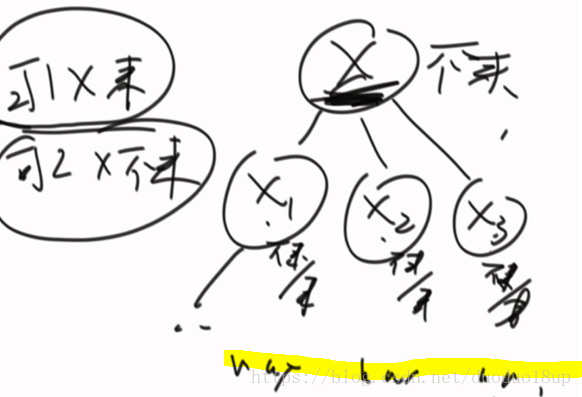
4.2 变体   结合实际例子

画图说明：

分析可能性：

1 节点X来的活跃度   

2  节点X不来的活跃度：   来/不来中选择最大的

代码实现：

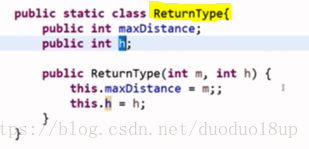
多叉树节点自定义：

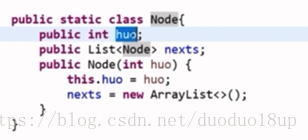
返回类型定义：

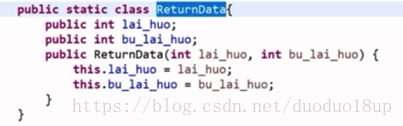
处理逻辑：

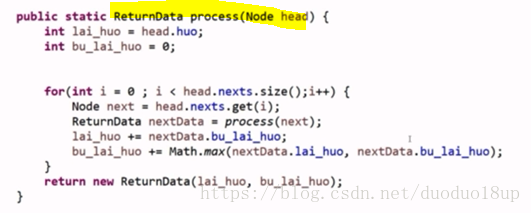
主函数：

4.3  总结：

先分析子树---再分析总树---把可能性列出来---视为黑盒---在解决黑盒----返回

注意basecase的情况~

4.4: 判断一棵树是否为平衡二叉树：

逻辑：