图的表示和遍历

来自《图解数据结构---使用Java》

图的表示常见到的有：

• 相邻矩阵法
• 相邻表法

（1）相邻矩阵法 

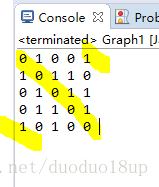
某个点arr[x][y]值为1则表示对应顶点有边存在，为0则表示对应顶点无边存在。 

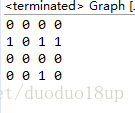
无向图（矩阵对称）   有向图（矩阵不对称）

package com.duoduo.day316;
/*无向图*/
public class Graph1 {

	public static void main(String [] args) {
		int[][] arr=new int[6][6];   //5个顶点 长度6
		int i,j,temp1,temp2;
		int [][] data= {{1,2},{2,1},{1,5},{5,1},{2,3},{3,2},{2,4},{4,2},{3,4},{4,3},{3,5},{5,3},{4,5},{5,4}};
		
		//初始化相邻矩阵
		for(i=0;i<6;i++) {
			for(j=0;j<6;j++) {
				arr[i][j]=0;
			}
		}
		
		
		//读取data矩阵信息 并将边信息填入arr矩阵
		for(int k=0;k<13;k++) {      //读取data
				temp1=data[k][0];
				temp2=data[k][1];
				arr[temp1][temp2]=1;
		}
		
		//输出矩阵
		for(i=1;i<6;i++) {
			for(j=1;j<6;j++) {
				System.out.print(arr[i][j]+" ");
			}
			System.out.println();
		}
	}
}
	

package com.duoduo.day316;
/**
 * 有向图

 * @author 多多
 *
 */
public class Graph {
	public static void main(String [ ] args) {
		int [][] arr=new int[5][5];   //4个顶点  1,2,3,4   声明矩阵
		int i,j,temp1,temp2;
		int[][] data= {{1,2},{2,1},{2,3},{2,4},{4,3}};  //图形各边的起始点和终点值
		
		//初始化相邻矩阵为0
		for( i=0;i<5;i++) {
			for( j=0;j<5;j++) {
				arr[i][j]=0;
			}
		}
		
		//读取边信息  填入arr矩阵 
		for(i=0;i<5;i++) {
			temp1=data[i][0];   //起始顶点
			temp2=data[i][1];   //终止顶点
			arr[temp1][temp2]=1; //有边的点填入1
		}
		
		//打印矩阵
		for(i=1;i<5;i++) {
			for(j=1;j<5;j++) {
				System.out.print(arr[i][j]+" ");
			}
			System.out.println();
		}
	
	}
}

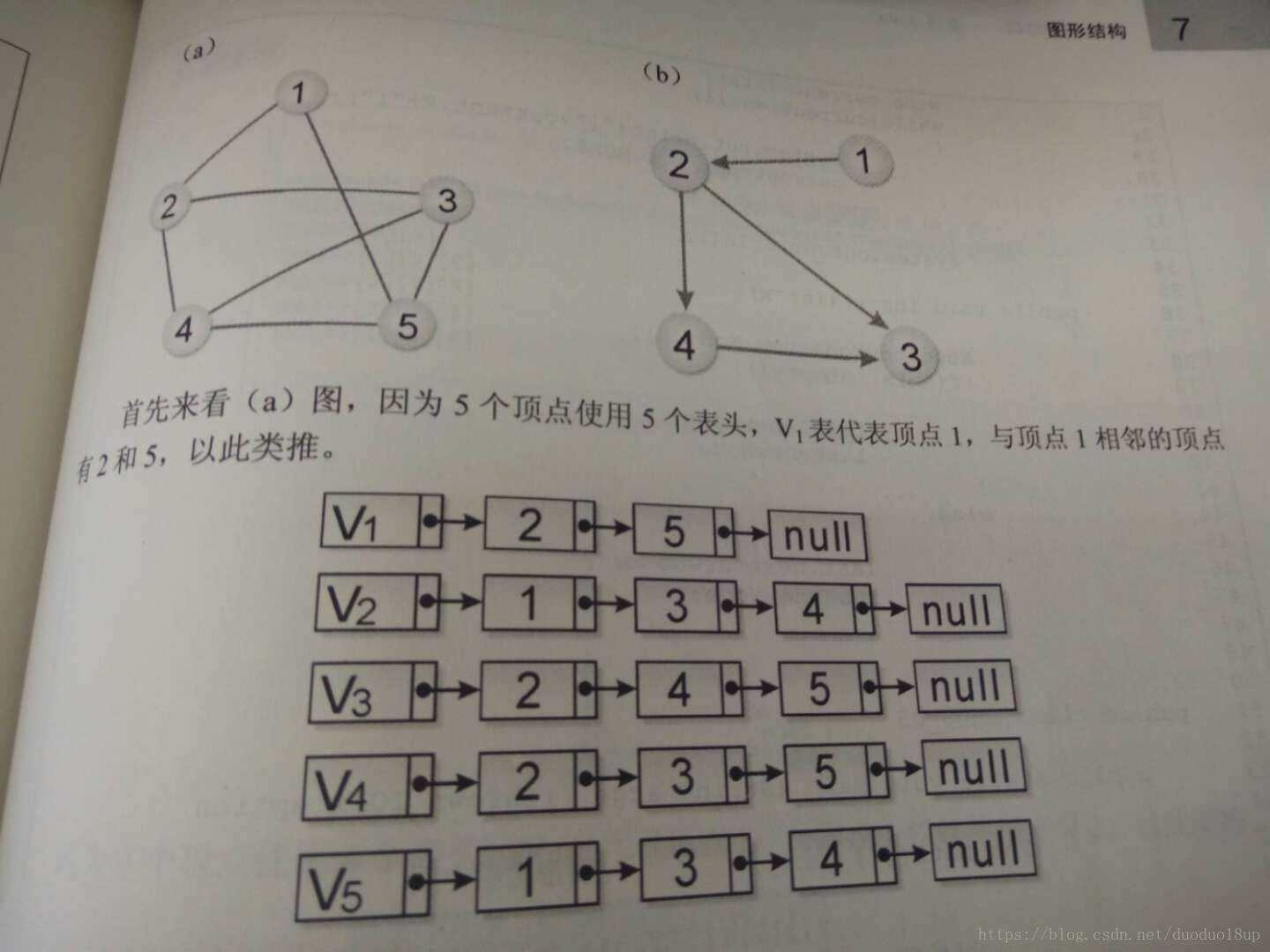
(2)相邻表法 

图形A有n个顶点，则用n个表（链表）来表示，每个顶点后面接着的表节点元素表示该顶点到该元素存在边，每个表的最后一个元素为null。

package com.duoduo.day316;
import com.duoduo.day316.Node;
/**
 * 相邻表法
 * 每一个顶点使用一个表
 * @author 多多
 *
 */
public class GraphLink {
	public  Node first;  //头节点
	public Node last;   //尾节点
	
	/*判断链表是否为空*/
	public  boolean isEmpty() {
		return first==null;
	}
	
	/*打印链表节点*/
	public void print() {
		Node current=first;
		while(current!=null) {
			System.out.print("["+current.data+"]");
			current=current.next;
		}
	System.out.println();
	}
	
	/*插入链表节点*/
	public void insert(int newData) {
		Node newNode=new Node(newData);   //新建节点
		//判断链表是否为空
		if(isEmpty()) {
			first=newNode;
			last=newNode;
		}else {
			last.next=newNode;
			last=newNode;
		}
	}
		
	
	public static void main(String [] args) {
		int[][] Data= {{1,2},{2,1},{1,5},{5,1},{2,3},{3,2},{2,4},{4,2},{3,4},{4,3},{3,5},{5,3},{4,5},{5,4}};
		int newData;                            //插入的新节点
		int i,j;
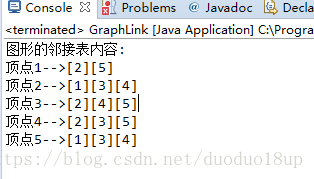
		System.out.println("图形的邻接表内容:");
		GraphLink [] head=new GraphLink[6];     //5个顶点  长度为6     储存顶点链表的数组
		for(i=1;i<6;i++) {                     //每个顶点建立一个单链表
			head[i]=new GraphLink();          
			System.out.print("顶点"+i+"-->"); 
			for(j=0;j<14;j++) {
				if(Data[j][0]==i) {             //若起始顶点为i时 
					newData=Data[j][1];         //则将终止节点视为新节点---插入至以i为起始顶点的单链表中
					head[i].insert(newData);
				}
			}
			head[i].print();
		}
	}
}