C++ 模拟实现 并查集

借用大佬的一句话来解释并查集：
你是我的朋友，那么你的朋友也可以是我的朋友

并查集的实现原理

并查集，也就是一些与集合有关的合并和查找操作。

如果我们相对一些由很多元素组成的不同的集合进行操作，然后按照一定的规律对一些集合进行合并，那么这时候就需要使用并查集来解决。

• 当我们按照图形的方式来看待的时候，他可以说是多叉树的结构
• 但是我们在存储的时候，缺可以使用数组的形式进行存储

有 0-9 一根10个数
0，1，2 是一个集合
3，4，5 是一个集合
6，7，8，9 是一个集合

那么使用并差集的结构，可以看成是这样的

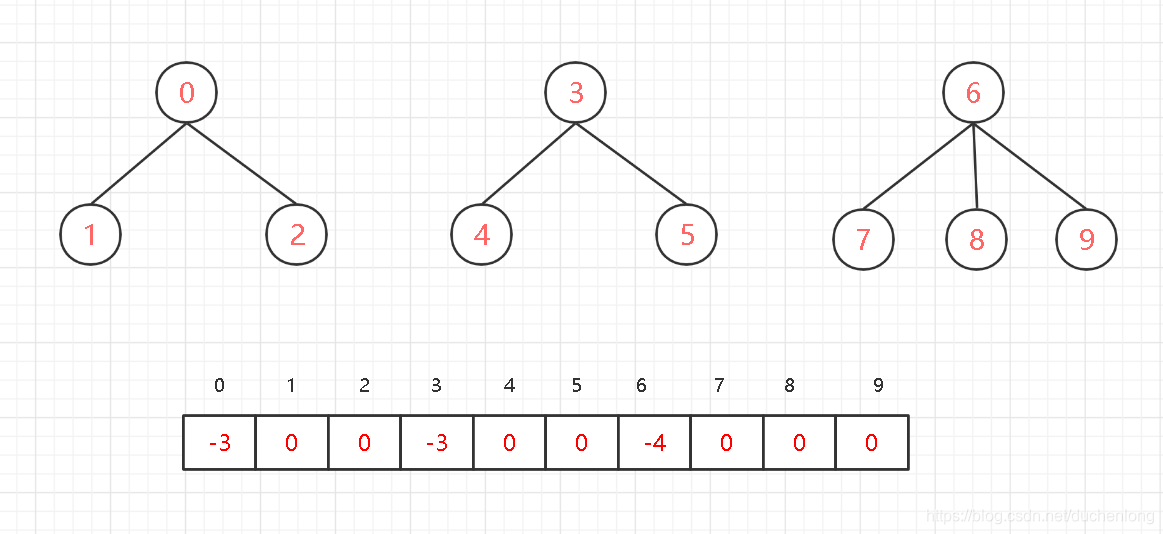
对于存储结构而言，我们可以在初始化的时候为每一个位置赋值为-1

1. 数组的下标对应集合中元素的编号
2. 数组中的数据如果为正数或者0，就表示该元素的双亲所在的位置
3. 数组中数据如果为负数，就表示当前位置是一个根节点，他的绝对值就是这棵树有多少个节点（包括自己）

并查集的描述

template<class T>
class unionFindSet
{
public:
	unionFindSet(const int size)
	{
		_ufs = vector<T> (size,-1);
	}

	//递归查找
	int Find_recu(const int pos);
	//迭代查找
	int Find_iter(const int pos);
	//合并
	bool Union(const int le, const int ri);
private:
	vector<T> _ufs;
};

查找

这里的查找并不是指查找这个节点，而是通过这个节点，找到他所在的这棵树的根节点

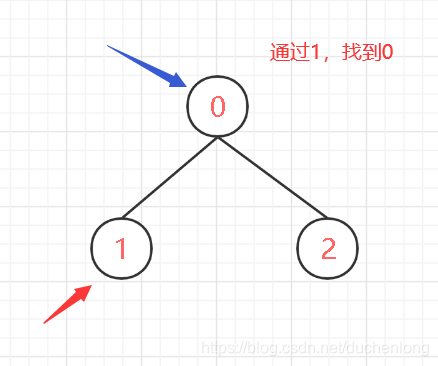
而我们所设计的并查集中，数组的下标如果为非负数，那么这个非负数就是他的双亲节点，我们只需要一直通过这个双亲节点，就可以迭代的找到整棵树的根节点

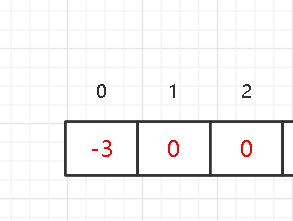
	//递归查找
	int Find_recu(const int pos)
	{
		if (_ufs[pos] >= 0)
			_ufs[pos] = Find(_ufs[pos]);
		return _ufs[pos];
	}

	//迭代查找
	int Find_iter(const int pos)
	{
		int res = _ufs[pos];
		while (res >= 0)
			res = _ufs[res];
		return res;
	}

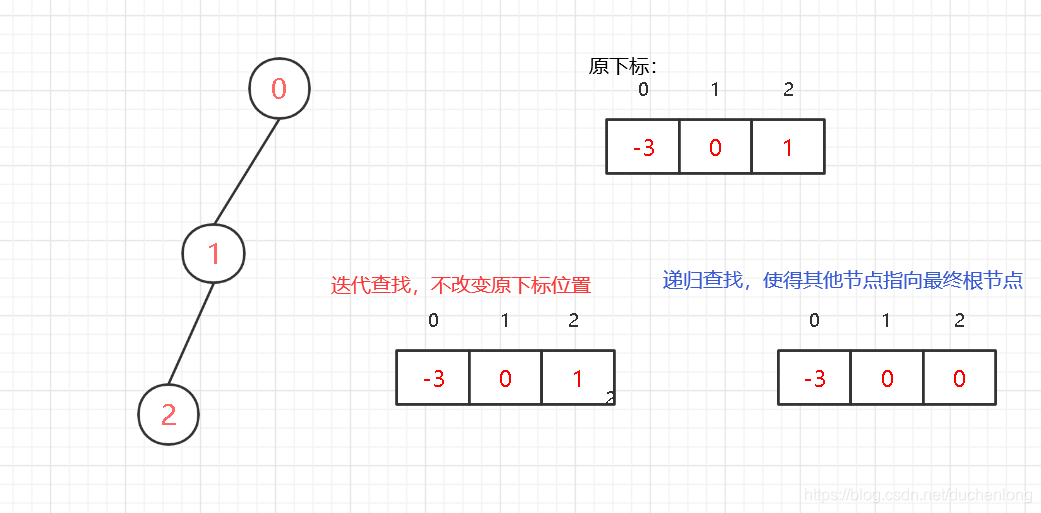
这里需要注意，同样都是遍历一次，如果我们需要方便下次更快的查找同一个节点，可以一步直接找到根节点，那么就可以采用这种递归的方式进行查找，或者采用迭代查找时，遍历两次。

使用迭代查找，只遍历一次，那么下次再通过同一个节点找他的根节点，那么所花费的时间不会减少。

合并

合并两个点，我们需要先确认这两个点所在的集合是否是同一个集合

• 如果是同一个集合，那么我们就无需合并
• 不是同一个集合，我们需要合并的就是两个集合的根节点了，按照实际情况决定合并后根节点的所在。

怎么确定是否是同一个集合呢？

对于并查集中的集合而言，唯一标识一个集合的就是他们的公共的根节点了，只需要通过查找操作找到这个根节点就可以了

/*
	 **		le_root ri_root			分别为两个节点的根节点的位置
	 **		le_root == ri_root	说明两个节点在同一棵树中，不需要进行合并
	 **
	 **		le_root != ri_root	说明不在同一棵树中，需要进行合并
	 **			le 位置需要 + ri位置所存节点个数;  再更新 ri 位置的根节点下标 为 le
	*/
	bool Union(const int le, const int ri)
	{
		int le_root = Find_iter(le);
		int ri_root = Find_iter(ri);

		if (le_root == ri_root)
			return false;

		_ufs[le] += _ufs[ri];
		_ufs[ri] = le;
		return true;
	}

一个并查集的类

template<class T>
class unionFindSet
{
public:
	unionFindSet(const int size)
	{
		_ufs = vector<T> (size,-1);
	}

	//递归查找
	int Find_recu(const int pos)
	{
		if (_ufs[pos] >= 0)
			_ufs[pos] = Find(_ufs[pos]);
		return _ufs[pos];
	}

	//迭代查找
	int Find_iter(const int pos)
	{
		int res = _ufs[pos];
		while (res >= 0)
			res = _ufs[res];
		return res;
	}

	/*
	 **		le_root ri_root			分别为两个节点的根节点的位置
	 **			le_root == ri_root	说明两个节点在同一棵树中，不需要进行合并
	 **
	 **			le_root != ri_root	说明不在同一棵树中，需要进行合并
	 **					le 位置需要 + ri位置所存节点个数;  再更新 ri 位置的根节点下标 为 le
	*/
	bool Union(const int le, const int ri)
	{
		int le_root = Find_iter(le);
		int ri_root = Find_iter(ri);

		if (le_root == ri_root)
			return false;

		_ufs[le] += _ufs[ri];
		_ufs[ri] = le;
		return true;
	}
private:
	vector<T> _ufs;
};