排序算法（三）

6、归并排序
原理：将两个及以上的有序表合并成一个有序表。将待排序列分成若干个序列，将各个小序列排成有序，最后合并将整个有序序列。基本思路，开始，将相邻两个元素合并成一个有序序列，然后，相邻两个序列再合并成一个有序序列，不断循环，直到整个序列合并为一个有序序列。
示例如下：

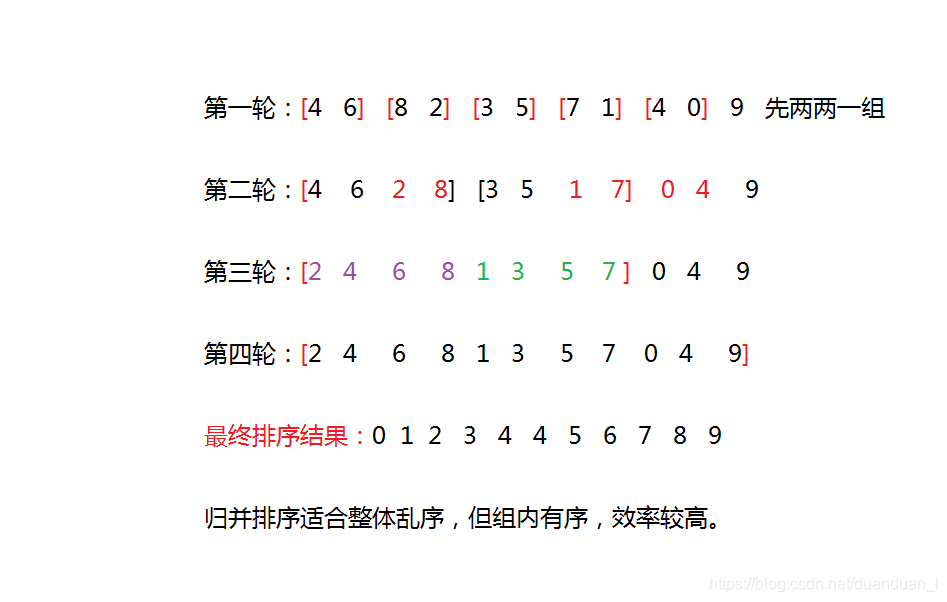
代码实现：

public class MergeSort {
    public static void merge(int[] arr,int left,int middle,int right){
        int[] brr = new int[arr.length];
        int mid = middle+1;
        int i = left;
        int j = left;
        while(left <= middle && mid <= right){//将两个数组中较小的数放到中间数组
            if(arr[left] <= arr[mid]){
                brr[j++] = arr[left++];
            }else{
                brr[j++] = arr[mid++];
            }
        }
        while(left <= middle){//将剩余部分放到中间数组
            brr[j++] = arr[left++];
        }
        while (mid <= right){
            brr[j++] = arr[mid++];
        }
        while(i <= right){//将中间数组放回原数组中
            arr[i] = brr[i++];
        }
    }
    public static void mergeSort(int[] arr,int left,int right){
        if(left < right){
            int middle = (left+right)/2;
            mergeSort(arr,left,middle);//左边递归
            mergeSort(arr,middle+1,right);//右边递归
            merge(arr,left,middle,right);//合并
        }
    }
    public static void main(String[] args){
        int[] arr = new int[]{3,0,6,9,7,4,0,1,4,8,2,6};//test
        mergeSort(arr,0,arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
}

算法分析：
(1)性能分析

(2)时间复杂度
归并排序的形式是一棵二叉树，它遍历的次数就是二叉树的深度，根据完全二叉树可以得到它的时间复杂度为O(Nlog2N)；
(3)稳定性
归并排序中，相等元素的前后顺序不会改变，所以它是一种稳定的算法。
(4)空间复杂度
在排序过程中，需要大小为N的空间保存整个序列，所以其空间复杂度为O(N)。
7、堆排序
原理：堆排序是一种树形排序算法，利用堆（顺序存储的完全二叉树）进行排序，利用大根堆（或小根堆）堆顶记录最大（或最小）的特征，使得在无序区中获得最大（或最小）记录变得简单。堆是一棵顺序存储的完全二叉树，若每个节点的值小于或等于其左右孩子节点的值，称为小根堆；每个节点大于等于其左右孩子节点的值，称为大根堆。
举例来说，对于序列{R1，R2，，，Rn}，满足下列条件之一，称为堆：
(1) 当Ri <= R2i+1 &&　Ri <= R2i+２，称为小根堆；　
(2) 当Ri ＞= R2i+1 &&　Ri ＞= R2i+２，称为大根堆；
思想：
(1) 将原始数组构建堆升序排列构建大根堆（降序排列构建小根堆），从最后一个节点开始调整，构建初始堆；
(2) 每一次交换R0和Rn，输出Rn（最大元素），再把剩下元素调整为大根堆，当输出最后一个元素，则排序完成（升序排列）。
举例如下：
初始序列为：{1,3,5,0,9,3,8,2,6,1}

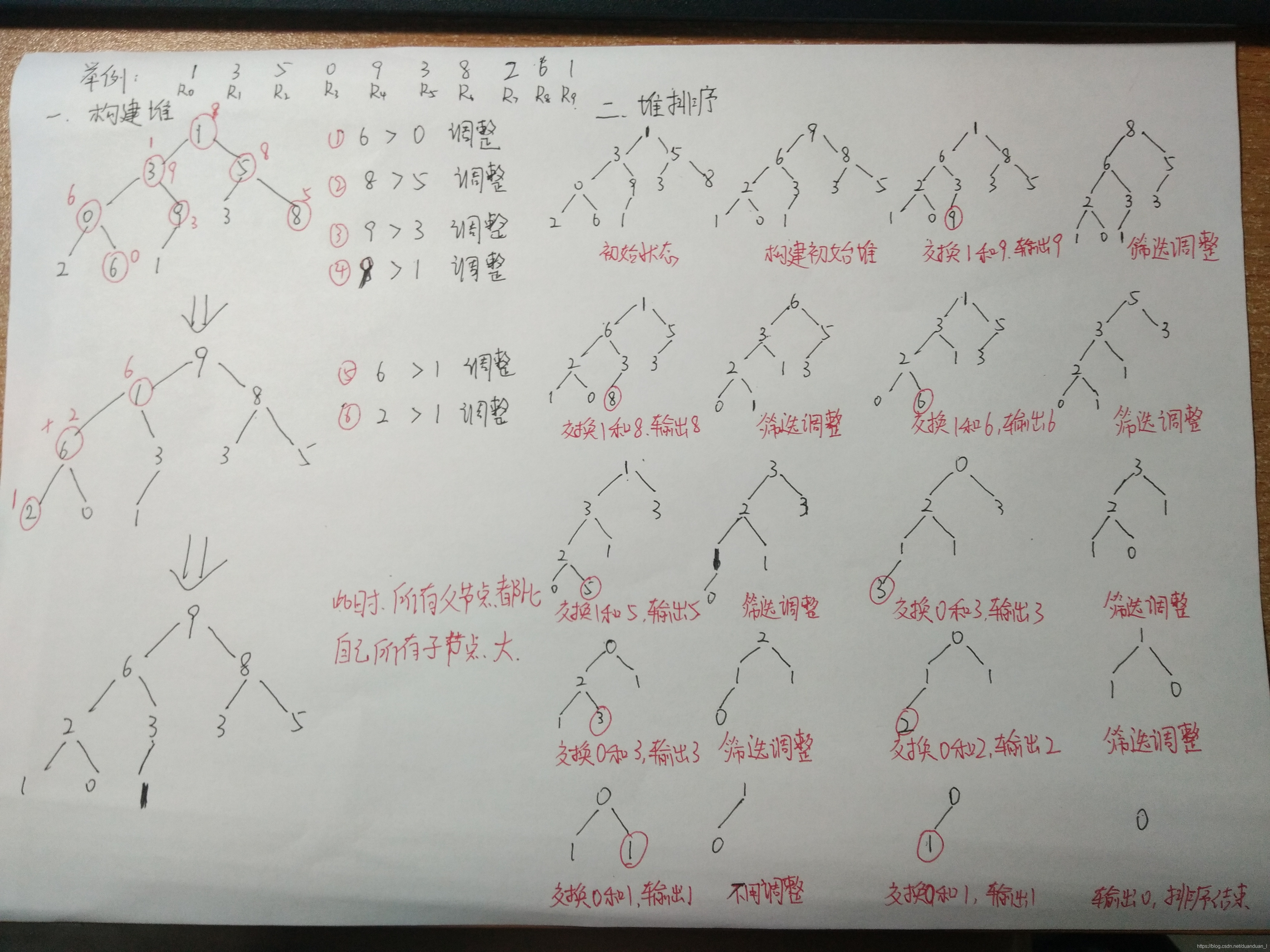
代码如下：

public class HeapSort {
    public static void headAdjust(int[] arr,int parent,int length){
        int temp = arr[parent];//temp保存父节点
        int child = 2*parent+1;//先获取左孩子
        while(child < length){
            //若一个节点有右孩子节点且右孩子节点的值大于左孩子节点，则取右孩子节点
            if(child+1 < length && arr[child+1] > arr[child]){
                child++;
            }
            //若父节点大于等于孩子节点的值，结束
            if(temp >= arr[child]){
                break;
            }
            arr[parent] = arr[child];
            //选取孩子节点的左孩子节点，继续向下筛选
            parent = child;
            child = 2*parent+1;
        }
        arr[parent] = temp;
    }
    public static void headSort(int[] arr){
        //循环建立初始堆
        for(int i = arr.length/2;i >= 0;i--){
            headAdjust(arr,i,arr.length);
        }
        //将最后一个元素与第一个元素交换
        for(int i = arr.length-1;i > 0;i--){
            int temp = arr[i];
            arr[i] = arr[0];
            arr[0] = temp;
            headAdjust(arr,0,i);//筛选调整
        }
    }
    public static void main(String[] args){
        int[] arr = new int[]{2,5,8,2,4,6,9,8,8,7,7,2};
        System.out.print("排序前：");
        System.out.println(Arrays.toString(arr));
        headSort(arr);
        System.out.print("排序后：");
        System.out.println(Arrays.toString(arr));
    }
}

算法分析：
(1)性能分析

(2)时间复杂度
堆的存储表示是顺序的（完全二叉树是顺序存储的），当需要对第k个最小的元素之前的部分序列进行排序，最好用堆排序。
(3)稳定性
堆排序是一种不稳定的算法，在筛选调整时，有可能对于相同的元素排在后面的交换到前面来。