leetcode - [字符串、动态规划] - （1）最大回文子串

1、问题描述

给定一个字符串s，求s得最长回文子串，你可以假设s得最大长度为1000。
例如：输入的字符串为"babad"，则输出最大的回文子串为"bab"和"aba"。

2、解题思路

• 边界条件：输入字符为空，直接返回空串；
• 思路1：最简单的方法，这道题可以分解为两个步骤：（1）求s的每一个子串p；（2）判断子串p是否为回文串。表示一个子串时，可以用它的起始、终止位置索引对（start，end）来表示。start表示该子串的起始位置，end表示该子串的终止位置。由于这样的索引对有$\frac{(n+1)n}{2}=n+(n-1)+...+1$对，所以步骤1花费的时间为$O(n^2)$，而判断每一个子串是否为回文串时，我们可以采用双指针来实现，花费的时间为$O(n)$，所以这种方法最终的时间复杂度为$O(n^3)$。
• 思路2：实际上，如果采用动态规划的方法，可以实现在$O(n^2)$的时间内完成回文串的判断，这种具体做法如下：
  （1）定义状态
  我们可以使用一个二维数组ispal来表示一个子串是否为回文串，数组的行坐标表示子串的起始位置，列坐标表示子串的终止位置，数组中元素的值表示以行坐标为起始位置，列坐标为终止位置的子串是否为回文串，例如ispal(0，1)=true表示起始位置为0，终止位置为1的子串为回文串，由于矩阵的终止位置一定大于或等于起始位置，所以矩阵的下三角元素值没有意义。
  （2）定义状态转移方程
  我们清楚这样一些事实：
  a、当子串只有1个字符时，它一定是回文字符串；
  b、当子串的长度超过2个字符时，如果s[l，r]是一个回文串，比如s[l,r]=“abccba”，则将这个回文串的两边（如果可以的话）各往里收缩一个字符之后形成的子串s[l+1，r-1]也一定是一个回文串。即如果s[l，r] == true，则s[l+1，r-1] ==true。
  由上面的的事实可知，当s[l]==s[r]，字符串s[l，r]是否为回文串完全由s[l+1，r-1]决定，但这里还需要考虑原字符串去除左右边界之后子串的边界情况：
  这里，我们要求s[l+1，r - 1]至少包含两个字符，才有必要继续判断下去，否则直接根据左右边界是否相等就能判断原字符串是否是回文串，而s[l+1，r-1]至少包含两个字符等价于l+1<r-1，即r-1>2，
  综合上述分析，最终的状态转移方程如下：
  $$ispal(l，r)=\{\begin{array}{ll}true& ifs[l]==s[r]andispal(l+1，r-1)==true)\\ false& others\end{array}$$
• 以"s=babad"为例，使用动态规划方法的过程如下：
• 

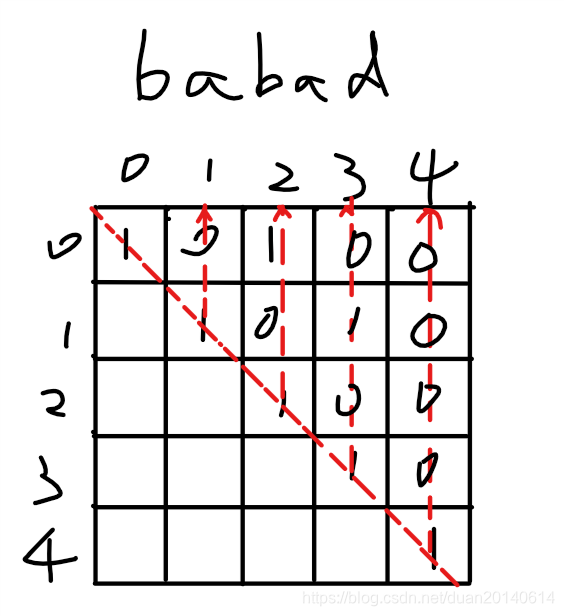
3、代码实现

class Solution:
    def longestPalindrome(self, s: str) -> str:
        
        longestp = ""
        
        if len(s) != 0:
            
            ispal =[[False] * len(s) for i in range(len(s))]
            
            for r in range(0,len(s)):
                for l in range(0,r + 1):
                    l = r - l
                    if r - l <= 2:
                        if s[l] == s[r]:
                            ispal[l][r] = True
                    else:
                        if s[l] == s[r] and ispal[l+1][r-1] == True:
                            ispal[l][r] = True
            
            max_len = 0                       
            for l in range(0,len(s)):
                for r in range(l,len(s)):
                    if r - l + 1 > max_len and ispal[l][r] == True:
                        max_len = r - l + 1
                        longestp = s[l: r + 1]
                        
            
        return longestp