本文探讨了正则化的逻辑回归，详细介绍了未正则化逻辑回归的代价函数及其正则化后的形式，并讲解了如何用梯度下降法解决正则化逻辑回归问题。
1、正则化的逻辑回归
（1）未正则化的逻辑回归的代价函数：
J(θ)=−1m∑i=1m[y(i)log(hθ(x(i))+(1−y(i))log(1−hθ(x(i)))]J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]J(θ)=−m1i=1∑m[y(i)log(hθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
（2）正则化的逻辑回归的代价函数：
J(θ)=−1m∑i=1m[y(i)log(hθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+12m∑j=1nθj2J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]+\frac{1}{2m}\sum_{j=1}^{n}\theta_{j}^{2}J(θ)=−m1i=1∑m[y(i)log(hθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2m1j=1∑nθj2
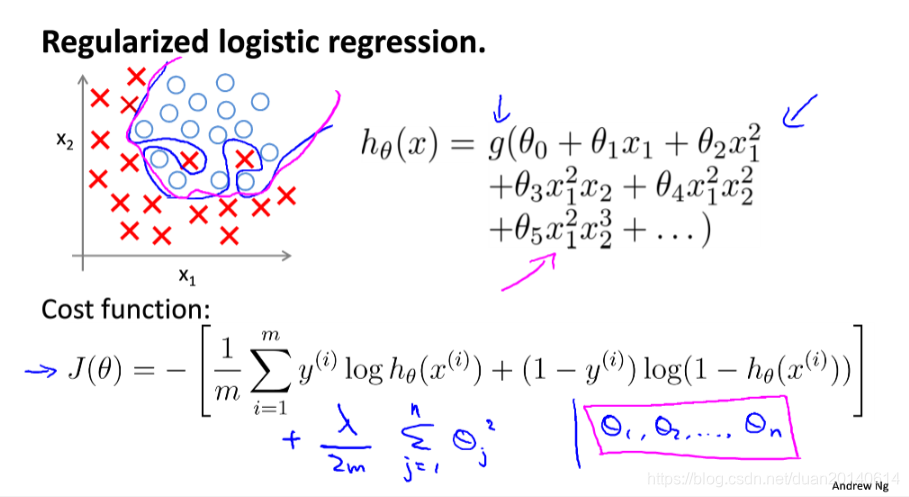
2、使用梯度下降法求解正则化的逻辑回归
正则化的和未正则化的逻辑回归模型的参数的更新公式和线性回归模型一样：
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
