32. 最长有效括号（未完待续）

思路

题目是要求给定一个字符串，求满足左右括号规范的最大连续子串。满足左右括号规范的常用手段可以计左括号为1，右括号为-1遍历到最后和是0则满足规范或者使用栈：将左括号push进去遇到右括号则弹出最后栈空则满足规范。
这个问题解决的思路有：思路一：定义一个二维数组dp[i][j]表示以第i个字符结尾最长有效括号的长度：其中i表示第i个字符，j表示在i之前的字符 。假如j+value>=0则可继续追加字符。
状态转移方程为：

dp[i+1][j+value] = max(dp[i][j]+1, 1)

结果超内存了。。代码如下：

class Solution {
    public int longestValidParentheses(String s) {
        int size = s.length();
        int [][] f = new int[size+1][size+1];
        for(int[] row: f) Arrays.fill(row, -1);
        int ret = 0;
        for(int i=0; i<size;i++){
            // 左括号为1，右括号则为-1
            int value  = 2*(s.charAt(i)=='('?1:0)-1;
           //初始化边界，当前一个左括号则值为1
            if(value==1) f[i+1][1] = 1;
            for(int j=0; j<size;j++){
                //如果当前子状态不为非法状态且左括号仍旧大于等于有括号则更新状态
                if(f[i][j]!=-1&&j+value>=0){
                    f[i+1][j+value] = Math.max(f[i][j]+1,1);
                    if(j+value==0) ret = Math.max(ret,f[i+1][j+value]);
                }
            }
        } 
        return ret;
    }
}

算法没啥问题，但很可惜不是最优的算法。那么能否只使用一维dp解决这个问题呢？答案是肯定的。
在上面使用的二维dp中我们用j表示前缀和，那么在一维dp中我们用dp[i]表示以i字符结尾的最长连续有效括号串，在计算前缀和过程中对结果进行剪枝。
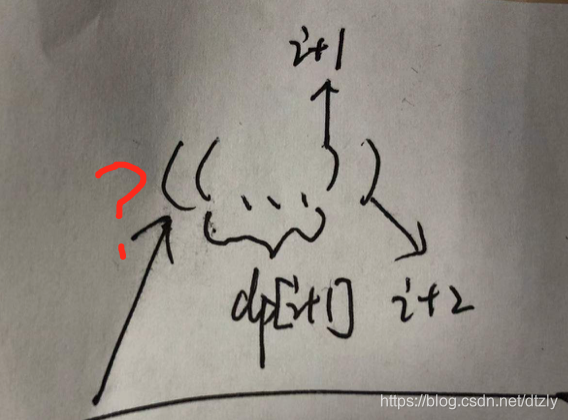
1）那么第i+2个字符是左括号显然不构成有效括号，dp[i+2]=0 . 2)如果第i+2个字符是右括号就转化为dp[i+2] = dp[i]+2 . 3)若第i+1字符是右括号，那么需要判断第i+1字符是不是左括号如下图所示，问号字符即i+2处右括号对应的左括号为i+2-dp[i+1]-2=i-dp[i+2]那么状态转移则转化为： dp[i+2] = dp[i + 1] + 2 + dp[i-dp[i + 1]]

class Solution {
   public int longestValidParentheses(String s) {
        int ret = 0;
        s =  " "+s;
        int dp[] = new int[s.length()];
        for (int i = 0; i < s.length()-2; i++) {
            if (s.charAt(i+2) == ')') {
                if (s.charAt(i + 1) == '(') {
                    dp[i+2] = dp[i] + 2;
                } else if (s.charAt(i +1- dp[i + 1] ) == '(') {
                    dp[i+2] = dp[i + 1] + 2 + dp[i-dp[i + 1]];
                }
                ret = Math.max(ret, dp[i+2]);
            }
        }
        return ret;
    }

}