1.Stockbroker Grapevine
股票经纪人以对谣言的过度反应而闻名。您被委托开发一种在股票经纪人中传播虚假信息的方法,以便为您的雇主在股市中提供战术优势。为了达到最佳效果,您必须以最快的方式传播这些谣言。
不幸的是,股票经纪人只信任来自他们“可信来源”的信息。这意味着在开始传播谣言时,您必须考虑他们的联系人结构。特定股票经纪人将谣言传递给每位同事需要一定的时间。您的任务是编写一个程序,告诉您选择哪位股票经纪人作为谣言的起点,以及谣言在股票经纪人社区传播所需的时间。此持续时间是指最后一个人收到信息所需的时间。
输入
您的程序将输入不同股票经纪人的数据集。每个数据集以一行开始,包含股票经纪人的数量。接下来是每位股票经纪人的一行,包含他们联系的人员数量、这些人员的身份以及他们将信息传递给每个人所需的时间。每位股票经纪人行的格式如下:该行以联系人数量(n)开头,后跟n对整数,每对对应一个联系人。每对中首先列出一个数字,表示联系人(例如,‘1’表示数据集中第一位人员),接着是传递信息给该人员所需的时间(以分钟为单位)。没有特殊的标点符号或空格规则。
每个人的编号从1到股票经纪人的数量。传递信息所需的时间在1到10分钟(含)之间,联系人数量在0到少于股票经纪人数量之间。股票经纪人的数量范围从1到100。输入以包含0(零)人的股票经纪人集结束。
输出
对于每组数据,您的程序必须输出一行,包含导致信息传递最快的人员,以及在将信息交给该人员后,最后一个人收到任何给定信息所需的时间,以整数分钟计。您的程序可能会接收到一个排除某些人员的连接网络,即某些人可能无法到达。如果您的程序检测到这种断开的网络,简单地输出消息“disjoint”。请注意,从A人传递信息到B人所需的时间不一定与从B人传递到A人所需的时间相同,如果这种传输可能的话。
思路:
此题是一道很典型的多元求最短路径的问题,我们将使用Dijkstra算法来计算每个节点作为起点的最短路径,并确定传播时间。首先构建邻接表,无法直接连接的两点以inf(无穷大标记),记录可直接连接的两点的距离,在找一个中转点判断经过中转点后两点间距离是否会减少,如果减少则更新,在此过程中,可能存在一个点多次经过的情况,所以当所有点都遍历之后,可以获得某两点间的最短路径,详情可参考以下网址数据结构与算法(7-4)最短路径(迪杰斯特拉(Dijkstra)算法、弗洛伊德(Floyd)算法)_dikstra-优快云博客
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#define s 120
#define inf 0x3f3f3f3f
int D[s][s],n,t;
void floyd()
{
int begin,end,medium;
for(medium=1;medium<=t;medium++)
{
for(begin=1;begin<=t;begin++){
for(end=1;end<=t;end++)
{
if(medium==begin||medium==end||begin==end)continue;
if(D[begin][medium]+D[medium][end]<D[begin][end])
{
D[begin][end]=D[begin][medium]+D[medium][end];
}
}
}
}
}
int main()
{
int i,j,k,d,tt;
while(~scanf("%d",&t)&&t)
{
memset(D,inf,sizeof(D));
for(i=1;i<=t;++i)
{
D[i][i]=0;
scanf("%d",&n);
while(n--){
cin>>d>>tt;
D[i][d]=tt;
}
}
floyd();
int min=inf,max,flag;
for(i=1;i<=t;i++)
{
max=0;
for(j=1;j<=t;j++){
if(D[i][j]>max)
max=D[i][j];
}
if(max<min){
min=max;
flag=i;
}
}
if(min==inf)
printf("disjoint\n");
else
printf("%d %d\n",flag,min);
}
return 0;
}
2.树的直径
一棵树的直径就是这棵树上存在的最长路径。现在有一棵 nn 个节点的树,现在想知道这棵树的直径包含的边的个数是多少?
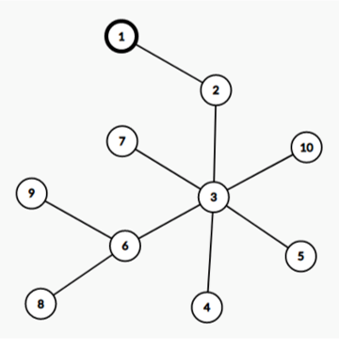
如图所示的数据,这棵树的直径为 (1−2−3−6−9)(1−2−3−6−9) 这条路径,包含的边的个数为 44 ,所以答案是 44 。
Input
第 11 行:一个整数 nn ,表示树上的节点个数。 (1≤n≤100000)(1≤n≤100000)
第 2∼n2∼n 行:每行有两个整数 u,vu,v 表示 uu 与 vv 之间有一条路径。 (1≤u,v≤n)(1≤u,v≤n)
Output
输出一个整数,表示这棵树直径所包含的边的个数。
思路:
-
任选一个节点作为起点:从树中任意选择一个节点(例如节点1)作为起点。
-
找到距离起点最远的节点:使用广度优先搜索(BFS)或深度优先搜索(DFS)从起点出发,找到距离起点最远的节点,记为节点
A。 -
找到距离节点
A最远的节点:再次使用 BFS 或 DFS 从节点A出发,找到距离A最远的节点,记为节点B。 -
计算直径:节点
A和节点B之间的路径就是树的直径,路径上的边的个数就是直径的长度。
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e5 + 10;
vector<int> son[N];
int rt[N], dp[N];
int n;
int DP(int r)
{
dp[r] = 0;
int m1 = 0, m2 = 0;
for(auto x: son[r])
{
DP(x);
if(dp[x]+1 > m1)
{
m2 = m1;
m1 = dp[x] + 1;
}
else
{
m2 = max(m2, dp[x] + 1);
}
}
dp[r] = m1;
return m1 + m2;
}
int main()
{
cin >> n;
for(int i=0; i<n-1; i++)
{
int x, y;
cin >> x >> y;
rt[y]++;
son[x].push_back(y);
}
int r = 0;
for(int i=1; i<= n; i++)
{
if(!rt[i])
{
r = i;
break;
}
}
cout << DP(r);
return 0;
}3.Invitation Cards
在电视时代,参加剧院表演的人并不多。马利丁西亚的古董喜剧演员意识到了这一点。他们希望传播剧院,尤其是古董喜剧。他们印制了包含所有必要信息和节目安排的邀请卡。许多学生被雇来在公众中分发这些邀请函。每位学生志愿者被分配了一个特定的公交站,他们整天待在那里,向乘坐公交的人发放邀请函。学生们参加了一门特殊课程,学习如何影响他人,以及影响与抢劫之间的区别。
交通系统非常特别:所有线路都是单向的,并且连接恰好两个站点。公交车每半小时从出发站出发,载着乘客。到达目的地后,公交车空车返回出发站,等待下一个整点半,例如 X:00 或 X:30,其中 'X' 表示小时。两个站点之间的交通费用由特殊表格给出,并且需当场支付。线路的规划方式是,每个往返(即从同一站点出发并返回)都经过一个中央检查站(CCS),每位乘客都必须经过全面检查,包括身体扫描。
所有 ACM 学生成员每天早上从 CCS 出发。每位志愿者都要前往一个预定的站点邀请乘客。志愿者的数量与站点数量相同。一天结束时,所有学生都会返回 CCS。你需要编写一个计算机程序,帮助 ACM 最小化每天为其员工的交通费用。
输入
输入由 N 个案例组成。第一行仅包含一个正整数 N。接下来是各个案例。每个案例以一行开始,包含恰好两个整数 P 和 Q,1 <= P,Q <= 1000000。P 是站点的数量,包括 CCS,Q 是公交线路的数量。然后有 Q 行,每行描述一条公交线路。每条线路包含恰好三个数字 - 出发站、目的站和价格。CCS 用数字 1 表示。价格为正整数,其总和小于 1000000000。你还可以假设从任何站点到任何其他站点总是可以到达。
输出
对于每个案例,打印一行,包含 ACM 每天为其志愿者的旅行费用所需支付的最小金额。
思路:
-
图的表示:将公交线路表示为有向图,其中站点是节点,公交线路是边,边的权重是交通费用。
-
最短路径计算:
-
使用Dijkstra算法计算从CCS(站点1)到所有其他站点的最短路径。
-
使用Dijkstra算法计算从所有其他站点返回到CCS的最短路径。为了计算返程的最短路径,我们需要将图反转(即所有边的方向反转),然后从CCS出发计算最短路径。
-
-
总成本计算:对于每个站点,将从CCS到该站点的最短路径成本加上从该站点返回到CCS的最短路径成本,得到该站点的总成本。然后将所有站点的总成本相加,得到每天的最小交通费用。
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pii; // {distance, node}
// 自定义比较结构体,用于实现最小堆
struct Compare {
bool operator()(const pii& a, const pii& b) {
return a.first > b.first; // 小顶堆
}
};
vector<ll> dijkstra(const vector<vector<pii>>& graph, ll start, ll n) {
vector<ll> dist(n + 1, LLONG_MAX);
dist[start] = 0;
priority_queue<pii, vector<pii>, Compare> heap; // 使用自定义比较结构体
heap.push({0, start});
while (!heap.empty()) {
ll current_dist = heap.top().first;
ll u = heap.top().second;
heap.pop();
if (current_dist > dist[u]) continue;
for (const auto& edge : graph[u]) {
ll v = edge.first;
ll weight = edge.second;
if (dist[v] > dist[u] + weight) {
dist[v] = dist[u] + weight;
heap.push({dist[v], v});
}
}
}
return dist;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
ll N;
cin >> N;
while (N--) {
ll P, Q;
cin >> P >> Q;
vector<vector<pii>> graph(P + 1);
vector<vector<pii>> reverse_graph(P + 1);
for (ll i = 0; i < Q; ++i) {
ll u, v, w;
cin >> u >> v >> w;
graph[u].push_back({v, w});
reverse_graph[v].push_back({u, w});
}
vector<ll> dist_from_ccs = dijkstra(graph, 1, P);
vector<ll> dist_to_ccs = dijkstra(reverse_graph, 1, P);
ll total_cost = 0;
for (ll i = 2; i <= P; ++i) {
total_cost += dist_from_ccs[i] + dist_to_ccs[i];
}
cout << total_cost << "\n";
}
return 0;
}4.战略游戏
Background
Bob 喜欢玩电脑游戏,特别是战略游戏。但是他经常无法找到快速玩过游戏的办法。现在他有个问题。
Description
他要建立一个古城堡,城堡中的路形成一棵无根树。他要在这棵树的结点上放置最少数目的士兵,使得这些士兵能瞭望到所有的路。
注意,某个士兵在一个结点上时,与该结点相连的所有边将都可以被瞭望到。
请你编一程序,给定一树,帮 Bob 计算出他需要放置最少的士兵。
Input
第一行一个整数 nn,表示树中结点的数目。
第二行至第 n+1n+1 行,每行描述每个结点信息,依次为:一个整数 ii,代表该结点标号,一个自然数 kk,代表后面有 kk 条无向边与结点 ii 相连。接下来 kk 个整数,分别是每条边的另一个结点标号 r1,r2,⋯ ,rkr1,r2,⋯,rk,表示 ii 与这些点间各有一条无向边相连。
对于一个 nn 个结点的树,结点标号在 00 到 n−1n−1 之间,在输入数据中每条边只出现一次。保证输入是一棵树。
Output
输出文件仅包含一个整数,为所求的最少的士兵数目。
思路:
本题是一道最小边覆盖问题,也叫数的最大独立集;一定要和最大点覆盖区分
本题可以考虑树形DP;设f[x][1]表示x节点放置士兵时,以x为根的子树需要的最少士兵数;f[x][0]表示x节点不放置士兵时,以x为根的子树需要的最少士兵数。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
bool c[1600],d[1600];
int tt[1600],a[1600][1600],f[1600][2],n,h=0;
void make()
{
int i,j;
memset(d,1,sizeof(d));
memset(c,1,sizeof(c));
for (i=1;i<=n;i++)
{
int x,k;
scanf("%d%d",&x,&k);
if (d[x]) {
tt[++h]=x; d[x]=false;
}
for (j=1;j<=k;j++)
{
int e;
scanf("%d",&e);
a[x][++a[x][0]]=e;
if (d[e]) {
tt[++h]=e; d[e]=false;
}
c[e]=false;
}
}
}
void dfs(int i)
{
if (a[i][0]==0)
{
f[i][1]=1; return;
}
int k;
for (k=1;k<=a[i][0];k++)
dfs(a[i][k]);
for (k=1;k<=a[i][0];k++)
{
f[i][0]+=f[a[i][k]][1];
f[i][1]+=min(f[a[i][k]][0],f[a[i][k]][1]);
}
f[i][1]+=1;
}
int main()
{
int i,he=0;
scanf("%d",&n);
make();
sort(tt+1,tt+h);
for (i=1;i<=h;i++)
if (c[tt[i]])
{
dfs(tt[i]);
he+=min(f[tt[i]][0],f[tt[i]][1]);
}
printf("%d",he);
}



















 957
957

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








