chapter 4 Beyond Gradient Desent
英语词汇
intracttable 棘手的,难以解决的
hundle 障碍
内容
主要讲述几种优化算法。
接下来探索局部最小值以及由此在训练网络中可能引起的问题。接着探索由于网络模型过深而引起的误差非凸面化,在这种情况下,小批量梯度下降算法失效。接着将探索非凸优化方法是如何克服这种问题的。
1. 误差曲面的非凸性
有很多的局部最小值,而神经网络需要找到全局最小值
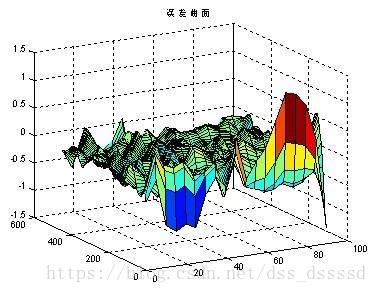
这个是题外话,了解一下阿偶:
* 模型唯一性

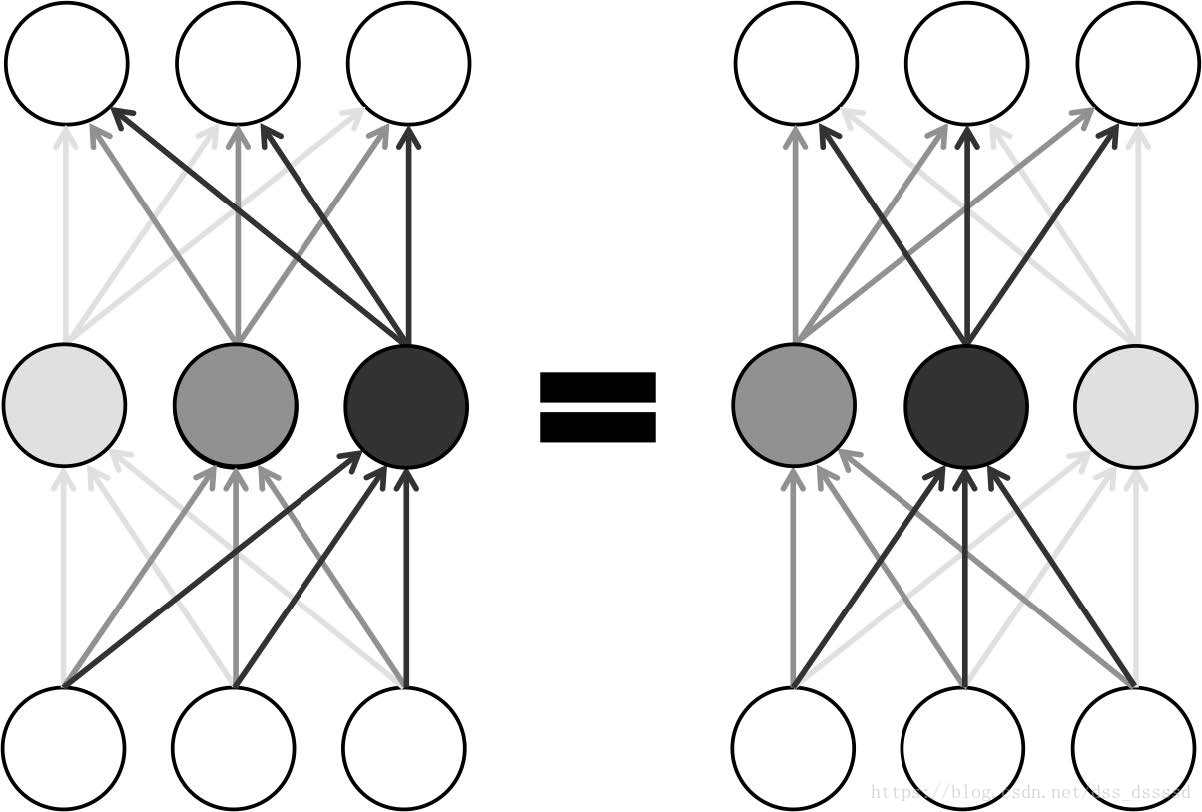
对于一个l层,每层有n个神经元的网络,有n!ln!l中安排参数的方法,最终网络的输出相同。
解决局部最小值的方法:
mini-batch gradient descent
蒙特卡洛方法
使用随机数(或更常见的伪随机数)来解决很多计算问题的方法,很经典的一个问题:利用投针实验求解圆周率ππ
二阶方法(second-order methods)
2. 学习比率的问题
学习速率调整(learning rate adaptation)
选择正确的学习速率很重要,学习速率过小,收敛速度过慢
学习速率太大, 直接忽略某些局部最小值
学习速率自适应调整(learning rate adaption):在训练过程中适当的修改学习速率来达到更好的收敛性
三个最流行的学习速率自调整算法
AdaGrad
利用每次迭代历史的梯度平方根的和来修改学习速率⨀⨀是矩阵的点乘,ϵϵ是初始学习速率
r0=0r0=0
ri=ri−1+gi⨀giri=ri−1+gi⨀gi
θi=θi−1−ϵδ⨁ri−−√⨀gθi=θi−1−ϵδ⨁ri⨀gδ≈10−7δ≈10−7避免除以0
python tensorflow调用代码:tf.train.AdagradOptimizer( learning_rate, initial_accumulator_valuer=0.1, use_locking=False, name='Adagrad' )在tensorflow中,δδ和initial_accumulator_valuer在一起.
- RMSProp
ri=ρri−1+(1−ρ)gi⨀giri=ρri−1+(1−ρ)gi⨀gi
衰退因子(decayfactor)(decayfactor) ρρ决定对历史梯度的保留程度
python tensorflow调用代码:
tf.train.RMSPropOptimizer( learning_rate, decay=0.9, momentum=0.0, epsilon=1e-10, use_locking=False, name='RMSProp' )- RMSProp
通过调整momentum来确定是否使用蒙特卡洛方法
RMSProp是一个非常高效的算法,对于很多的资深从业者而言是默认的选择
Adam 将蒙特卡洛和RMSProp结合起来
tf.train.AdamOptimizer( learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8, use_locking=False, name='Adam' )很先进高效
默认参数下已经表现的很好了,只需要修改参数learning_rate就好了。总结
最流行的算法:
- 误差曲面非凸
1. mini-batch gradient descent
2. mini-batch gradient with momentum
- 学习速率
- RMSProp
- RMSProp with momentum
- Adam
- 学习速率
主要是好的网络结构可以比训练算法有更好的效果,所有好的网络结构更值得花时间构建





 本文探讨了几种关键的优化算法,包括mini-batch gradient descent、RMSProp及其动量版本、以及Adam等,这些算法能够帮助神经网络克服局部最小值问题,并有效应对因网络深度增加导致的非凸误差曲面挑战。
本文探讨了几种关键的优化算法,包括mini-batch gradient descent、RMSProp及其动量版本、以及Adam等,这些算法能够帮助神经网络克服局部最小值问题,并有效应对因网络深度增加导致的非凸误差曲面挑战。
















 244
244

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








