两顶点之前有路径吗？ (20 分)

最新推荐文章于 2023-11-28 20:04:49 发布

原创最新推荐文章于 2023-11-28 20:04:49 发布 · 2.2k 阅读

10 ·

CC 4.0 BY-SA版权

PTA作业专栏收录该内容

5 篇文章

订阅专栏

一道题目探讨了判断两个顶点之间是否存在路径的问题，需要注意包括自身在内的路径情况。

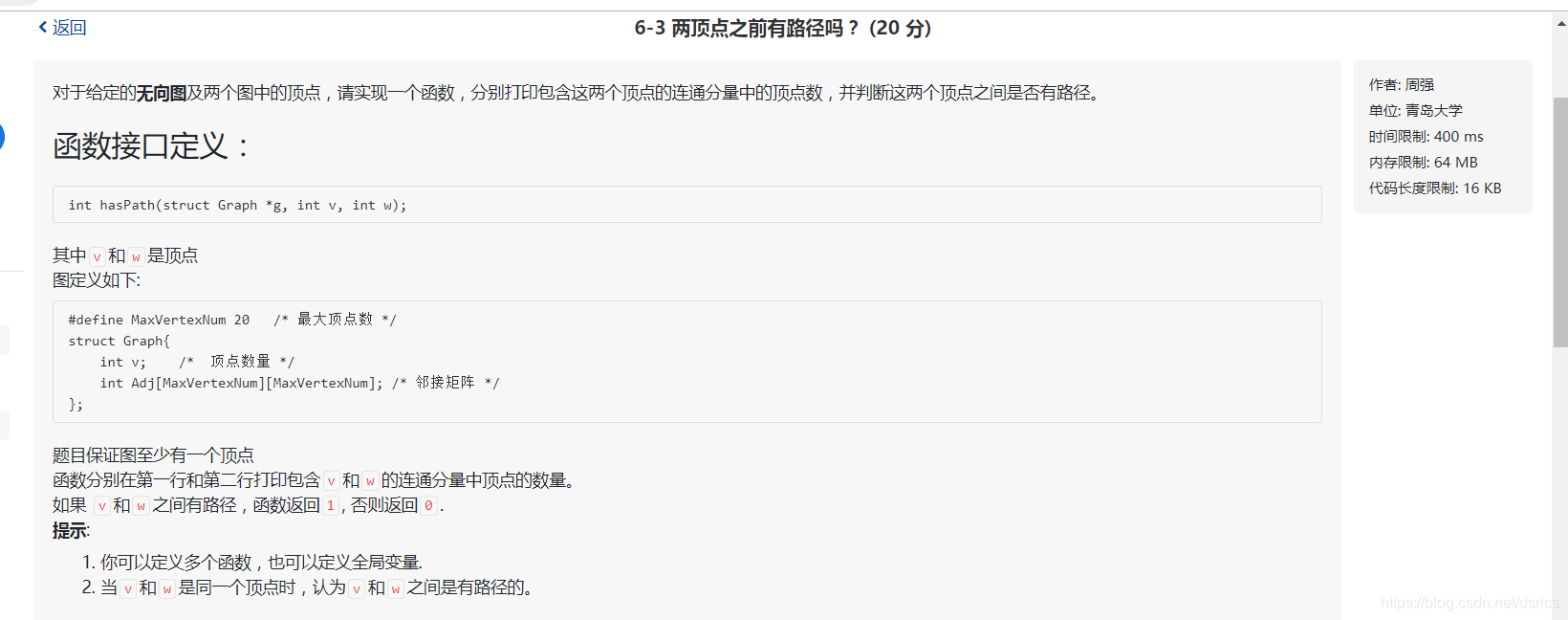
这道题有一个坑点在于自身是有路径的

int hasPath(struct Graph *g, int v, int w){
	for(int i=0;i<g->v;i++)g->Adj[i][i]=1;
	for (int i = 0; i < g->v; i++)
            {
                for (int j =0; j <g->v; j++)
                {
                	for(int l = 0;l<g->v;l++){
                		if (g->Adj[i][j] ==1&& g->Adj[l][j]==1)
                        g->Adj[i][l] =1;
					}
                    
                }
            }
    int sum=1;
    //ghy(g,0,v);
	for(int i=0;i<g->v;i++){
		if(g->Adj[v][i]==1){
			for(int j=0;j<g->v;j++){
				if(g->Adj[i][j]==1){
					g->Adj[v][j]=1;
				}
			}
		} 
	}
	for(int i=0;i<g->v;i++){
		if(g->Adj[v][i]==1&&v!=i){
			sum++;
		}
	} 
	printf("%d\n",sum);
	sum=1;
	for(int i=0;i<g->v;i++){
		if(g->Adj[w][i]==1){
			for(int j=0;j<g->v;j++){
				if(g->Adj[i][j]==1){
					g->Adj[w][j]=1;
				}
			}
		} 
	}
	for(int i=0;i<g->v;i++){
		if(g->Adj[w][i]==1&&w!=i)sum++;
	} 
	printf("%d\n",sum);
    if(g->Adj[v][w]==1)return 1;
    else return 0;
}