1. 二维数组的查找
描述
在一个二维数组array中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
给定 target = 7,返回 true。
给定 target = 3,返回 false。
public class Solution {
public boolean Find(int target, int [][] array) {
boolean flag = false;
for(int i =0; i < array.length;i++){
for(int j = 0; j < array[0].length;j++){
if(array[i][j] == target){
flag = true;
return flag;
}
}
}
return flag;
}
}
2. 替换空格
描述
请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param s string字符串
* @return string字符串
*/
public String replaceSpace (String s) {
return s.replaceAll(" ", "%20");// write code here
}
}
3. 从尾到头打印链表
描述
输入一个链表的头节点,按链表从尾到头的顺序返回每个节点的值(用数组返回)。
如输入{1,2,3}的链表如下图:

返回一个数组为[3,2,1]
0 <= 链表长度 <= 1000
/**
* public class ListNode {
* int val;
* ListNode next = null;
*
* ListNode(int val) {
* this.val = val;
* }
* }
*
*/
import java.util.ArrayList;
public class Solution {
public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
//将链表逆序,逆序之后的再放入集合
ArrayList<Integer> list = new ArrayList<Integer>();
ListNode pre = null;
ListNode cur = listNode;
while(cur != null){
ListNode nextNode = cur.next;
cur.next = pre;
pre = cur;
cur = nextNode;
}
ListNode res = pre;
while(res != null){
list.add(res.val);
res=res.next;
}
return list;
}
}
4. 重建二叉树
描述
给定某二叉树的前序遍历和中序遍历,请重建出该二叉树并返回它的头结点。
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建出如下图所示。

分析
二叉树的定义:
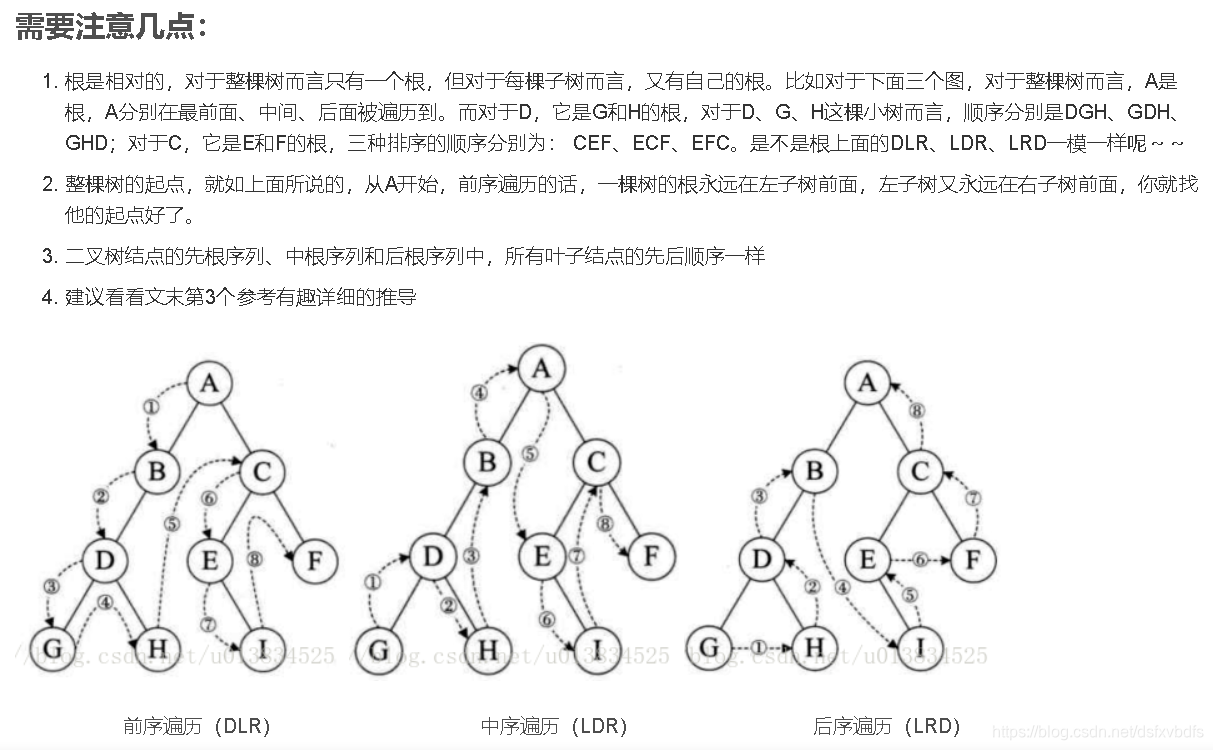
根据中序遍历和前序遍历可以确定二叉树,具体过程为:
- 根据前序序列第一个结点确定根结点
- 根据根结点在中序序列中的位置分割出左右两个子序列
- 对左子树和右子树分别递归使用同样的方法继续分解
例如:
前序序列{1,2,4,7,3,5,6,8} = pre
中序序列{4,7,2,1,5,3,8,6} = in
- 根据当前前序序列的第一个结点确定根结点,为 1
- 找到 1 在中序遍历序列中的位置,为 in[3]
- 切割左右子树,则 in[3] 前面的为左子树, in[3] 后面的为右子树
- 则切割后的左子树前序序列为:{2,4,7},切割后的左子树中序序列为:{4,7,2};切割后的右子树前序序列为:{3,5,6,8},切割后的右子树中序序列为:{5,3,8,6}
- 对子树分别使用同样的方法分解
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
import java.util.Arrays;
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
if (pre.length == 0 || in.length == 0) {
return null;
}
TreeNode root = new TreeNode(pre[0]);
// 在中序中找到前序的根
for (int i = 0; i < in.length; i++) {
if (in[i] == pre[0]) {
// 左子树,注意 copyOfRange 函数,左闭右开
root.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i + 1), Arrays.copyOfRange(in, 0, i));
// 右子树,注意 copyOfRange 函数,左闭右开
root.right = reConstructBinaryTree(Arrays.copyOfRange(pre, i + 1, pre.length), Arrays.copyOfRange(in, i + 1, in.length));
break;
}
}
return root;
}
}
5. 用两个栈实现队列
描述
用两个栈来实现一个队列,分别完成在队列尾部插入整数(push)和在队列头部删除整数(pop)的功能。 队列中的元素为int类型。保证操作合法,即保证pop操作时队列内已有元素。
示例:
输入:
["PSH1","PSH2","POP","POP"]
返回:
1,2
分析
注意队列和栈的区别:队列是FIFO,栈是FILO。
push操作就直接往stack1中push, pop操作需要分类一下:如果stack2为空,那么需要将stack1中的数据转移到stack2中,然后在对stack2进行pop,如果stack2不为空,直接pop就ok。
import java.util.Stack;
public class Solution {
Stack<Integer> stack1 = new Stack<Integer>();
Stack<Integer> stack2 = new Stack<Integer>();
public void push(int node) {
stack1.push(node);
}
public int pop() {
if (stack2.empty())
{
while (!stack1.empty())
{
stack2.push(stack1.lastElement());
stack1.pop();
}
}
int ret = stack2.lastElement();
stack2.pop();
return ret;
}
}




 本文精选了五个经典的编程题目,包括二维数组查找、字符串空格替换、链表逆序打印、二叉树重建及队列的栈实现。通过这些题目,读者可以深入理解数据结构的应用,并掌握相关算法的设计技巧。
本文精选了五个经典的编程题目,包括二维数组查找、字符串空格替换、链表逆序打印、二叉树重建及队列的栈实现。通过这些题目,读者可以深入理解数据结构的应用,并掌握相关算法的设计技巧。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








