11月26日学习小结

1.字符串的练习终于到头了，学长讲的那一道关于等腰三角形的蛇形矩阵，实在很难看得懂，我今天倒是研究出一种新的，简便的解题方法和思路，和大家分享一下：、

例题：

Spira 是一种螺旋，从 Spiral 演变过来的。 废话不多说，蒜头君决定称如下的等腰直角三角形为 Spira：

1 2 3 4 5
12 13 14 6
11 15 7
10 8
9

这个是腰长为 55 的时候的样子。 那么如果有其它腰长的 Spira 会是怎么样的呢？ 蒜头君想让你一个个画出来。

输入格式

第一行一个正整数 T（1 \the T \the 10） T （ 1 ≤ T ≤ 10 ） ，代表测试数据组数。

以下 TT 行，各行就一个正整数 N（2 \the N \the 1000）N （ 2 ≤ N ≤ 1000 ）       ，代表三角形腰长。

输出格式

对于每个测试数据，输出相应的 Spira。 每组数据之间以一个空行来间隔。

示例输入

2
5
4

示例输出

1 2 3 4 5
12 13 14 6
11 15 7
10 8
9

1 2 3 4
9 10 5
8 6
7

其实这道题的解题思路与蛇形矩阵思路类似，主要找数字变化规律，再自己找出数组下标的一种变化规律来使这些数字填进去，最后进行输出。

1.首先我们可以发下这些数字的变化规律是从一开始变化，先向右，再向左下方，再向上方，依次循环这个过程。

2.其次我们也要找到结束时最大数与我们要输入的n之间的关系，（这里其实有好的数学基础是很容易实现的，由此可以看出出数学在编程中的重要性），这里的假设每次填数的最大值是sum，那么sum与n之间的关系便是sum = n * (n+1)/2.

准备工作做完我们就需要敲代码了！

头文件及其变量声明

#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;
int main()
{
    int n,m,sum=0,i,j;
    int a[100][100]= {0};
    cin>>n;
    for(i=0; i<n; i++)
    {
        int x=0,k,y=0;
        sum = 1;
        cin>>m;
        a[0][0] = 1;

2.最重要的部分，我思想的 核心，给我仔细看！

大概思路如下：在前面我们已经定义了a[0][0]=1；那么接下来当sum<n*(n+1)/2时持续循环填数，

第一次进入第一个循环时x=0，y=0，我们的判断条件有两个，首先y+1<n，这是未了保证数组不越界，第二个条件是!a[x][y+1],这是为了检测下一个我们准备填的数组元素有没有被填过，因为我没最开始将数组a全部赋值为零，这里如果没有填过数，那么便是！0，即为真，循环可继续进行，但如果没有填过数，那么就是0，表达式为假，循环截止，所以这两个条件配合使用，可以是我们的数组完美的填上等腰三角形似的蛇形矩阵！

 while(sum<m*(m+1)/2)
        {
            while(y+1<m&&!a[x][y+1])  a[x][++y]=++sum;
            while(x+1<m&&y-1>-1&&!a[x+1][y-1]) a[++x][--y] =++sum;
            while(x-1>-1&&!a[x-1][y]) a[--x][y] = ++sum;
        }

最后一步，输出（不需要过多解释吧）

for(j=0; j<m; j++)
        {
            for(int k=0; k<m; k++)
            {
                if(a[j][k] !=0)
                    cout<<a[j][k]<<" ";
            }
            cout<<endl;
        }
        cout<<endl;
    }

接下来，我们看一看结果。

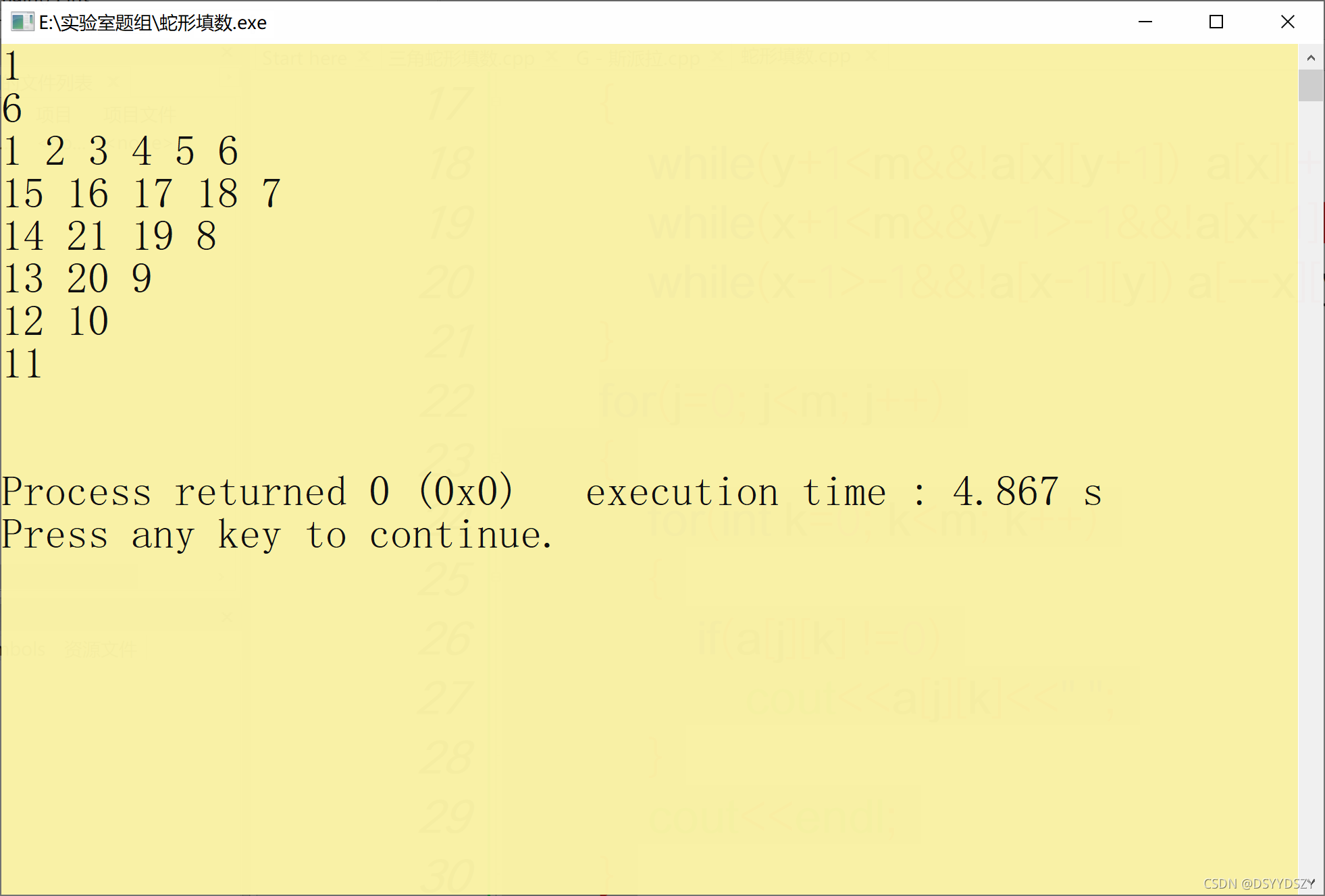
 2.练习结构体，并且解决了一道结构体的题目。（留着明天写吧，今天时间不早了，还要刷一会网站上的题，毕竟明天菜鸟杯了嘛）。