本文深入讲解了栈、队列、双端队列等基本数据结构的原理与Python实现方法，探讨了括号匹配、十进制转二进制、中缀表达式转后缀表达式等问题，并介绍了回文检查等应用。
基本数据结构
Contents
栈
简介
- 栈，队列，deques, 列表是一类数据的容器，它们数据项之间的顺序由添加或删除的顺序决定。
- 栈（有时称为“后进先出栈”）是一个项的有序集合
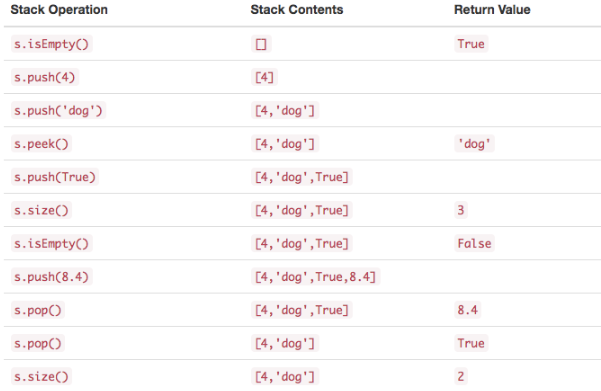
- 栈的抽象数据类型：
- Stack() 创建一个空的新栈。 它不需要参数，并返回一个空栈。
- push(item)将一个新项添加到栈的顶部。它需要 item 做参数并不返回任何内容。
- pop() 从栈中删除顶部项。它不需要参数并返回 item 。栈被修改。
- peek() 从栈返回顶部项，但不会删除它。不需要参数。 不修改栈。
- isEmpty() 测试栈是否为空。不需要参数，并返回布尔值。
- size() 返回栈中的 item 数量。不需要参数，并返回一个整数。
Python实现栈
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self,item):
self.items.append(item)
def pop(self):
self.items.pop()
def peek(self):
return self.items.pop()
def size(self):
return len(self.items)# 创建一个空栈
s = Stack()
print s.isEmpty()True
s.push(4)
s.push('dog')
s.items[4, 'dog']
简单括号匹配
给出一个表达式(5+6)∗(7+8)/(4+3)，如何判断它的括号是否匹配,给出一个空栈，如果是’(‘就入栈,如果是’(‘就出栈，最后的栈如果是空栈则括号匹配，否则不匹配
from pythonds.basic.stack import Stack
def parChecker(symbolString):
s = Stack()
balanced = True
index = 0
while index < len(symbolString) and balanced:
symbol = symbolString[index]
if symbol == "(":
s.push(symbol)
elif symbol == ")":
# 空栈不能弹栈
if s.isEmpty():
balanced = False
else:
s.pop()
index = index + 1
# 两个条件，前面的"("匹配成功并且s为空栈
if balanced and s.isEmpty():
return True
else:
return False
print(parChecker('(2((3)2))'))
print(parChecker('(2(3)'))
print(parChecker('((((2(3)'))True
False
False
符号匹配
在 Python 中，方括号 [ 和 ] 用于列表，花括号 { 和 } 用于字典。括号 ( 和 ) 用于元祖和算术表达式。只要每个符号都能保持自己的开始和结束关系，就可以混合符号
from pythonds.basic.stack import Stack
def parChecker(string):
s = Stack()
balanced = True
index = 0
while index<len(string) and balanced:
symbol = string[index]
if symbol in "([{":
s.push(symbol)
elif symbol in ")}]":
if s.isEmpty():
balanced = False
else:
top = s.pop()
if not matches(top,symbol):
balanced = False
index += 1
if balanced and s.isEmpty():
return True
else:
return False
def matches(open,close):
opens = "([{"
closers = ")]}"
return opens.index(open) == closers.index(close)
print(parChecker('{{([][])}()}'))
print(parChecker('[{()]'))
True
False
十进制转换成二进制
- “除 2”算法，它用栈来跟踪二进制结果的数字。 第一个余数实际上是序列中的最后一个数字,同样第二个余数就是序列倒数第二个数字…
//是取商，%是取余
from pythonds.basic.stack import Stack
def divideBy2(number):
remstack = Stack()
while number>0:
rem = number%2
# 入栈
remstack.push(rem)
number //= 2
binString = ''
while not remstack.isEmpty():
# 出栈
binString += str(remstack.pop())
return binString
print divideBy2(7)
print divideBy2(43)
print divideBy2(6)111
101011
110
更进一步，将基数2变为任意基数2-16
def baseConverter(number,base):
digits = "0123456789ABCDEF"
remstack = Stack()
while number > 0:
rem = number%base
remstack.push(rem)
number //= base
newString = ''
while not remstack.isEmpty():
newString += digits[remstack.pop()]
return newString
print(baseConverter(30,2))
print(baseConverter(30,16))11110
1E
中缀前缀和后缀表达式
我们生活中一般接触到的都是中缀运算符，所以不作介绍，而前缀和后缀运算符与中缀运算符的转换见下表：
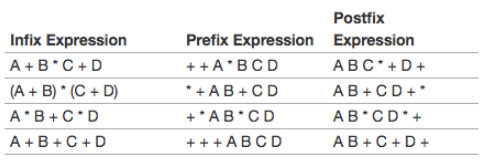
- 前缀运算符的运算顺序从后面一个运算符开始计算，使用运算符后面的操作数
- 后缀运算符的运算顺序从前面一个运算符开始计算，使用运算符前面的操作数
- 前后中运算符的遍历就如同前后中序遍历
- 操作数相对位置不变
中缀转后缀算法
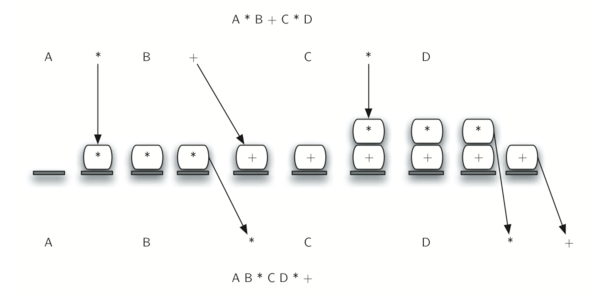
假设中缀表达式是一个由空格分隔的标记字符串。 操作符标记是*，/，+和 - ，以及左右括号。操作数是单字符 A，B，C 等。 以下步骤将后缀顺序生成一个字符串:
* 创建一个名为 opstack 的空栈以保存运算符。给输出创建一个空列表。
* 通过使用字符串方法拆分将输入的中缀字符串转换为标记列表。
* 从左到右扫描标记列表。
* 如果标记是操作数，将其附加到输出列表的末尾。
* 如果标记是左括号，将其压到 opstack 上。
* 如果标记是右括号，则弹出 opstack，直到删除相应的左括号。将每个运算符附加到输出列表的末尾。
* 如果标记是运算符，*，/，+或 -，将其压入 opstack。但是，首先删除已经在 opstack 中具有更高或相等优先级的任何运算符，并将它们加到输出列表中。
* 当输入表达式被完全处理时，检查 opstack。仍然在栈上的任何运算符都可以删除并加到输出列表的末尾。
from pythonds.basic.stack import Stack
def infixToPostfix(infixexpr):
# 优先级字典
prec = {}
prec["*"] = 3
prec["/"] = 3
prec["+"] = 2
prec["-"] = 2
prec["("] = 1
opStack = Stack()
postfixList = []
# 空格分隔的表达式
tokenList = infixexpr.split()
for token in tokenList:
# 操作数
if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token in "0123456789":
postfixList.append(token)
# 括号
elif token == "(":
opStack.push(token)
elif token == ")":
topToken = opStack.pop()
while topToken != '(':
postfixList.append(topToken)
topToken = opStack.pop()
# 操作符
else:
# 栈顶优先级大于当前操作符，并且栈不为空，弹栈加入输出列表
# 并且将当前操作符入栈
while (not opStack.isEmpty()) and (prec[opStack.peek()] >= prec[token]):
postfixList.append(opStack.pop())
opStack.push(token)
# 操作符栈不为空，全部弹出并加入输出链表
while not opStack.isEmpty():
postfixList.append(opStack.pop())
# 以空格为界加上去
return " ".join(postfixList)
print(infixToPostfix("A * B + C * D"))
print(infixToPostfix("( A + B ) * C - ( D - E ) * ( F + G )"))A B * C D * +
A B + C * D E - F G + * -
后缀表达式求值
例如计算：4 5 6 * +
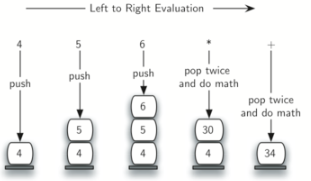
思路：
假设后缀表达式是一个由空格分隔的标记字符串。 运算符为*，/，+和 -，操作数假定为单个整数值。 输出将是一个整数结果。
- 创建一个名为 operandStack 的空栈。
- 拆分字符串转换为标记列表。
- 从左到右扫描标记列表。
- 如果标记是操作数，将其从字符串转换为整数，并将值压到operandStack。
- 如果标记是运算符
*，/，+或-，它将需要两个操作数。弹出operandStack 两次。 第一个弹出的是第二个操作数，第二个弹出的是第一个操作数。执行算术运算后，将结果压到操作数栈中。 - 当输入的表达式被完全处理后，结果就在栈上，弹出 operandStack 并返回值。
- 用于计算后缀表达式的完整函数见 ActiveCode 2，为了辅助计算，定义了一个函数 doM
from pythonds.basic.stack import Stack
def postfixEval(postfixExpr):
openrandStack = Stack()
tokenList = postfixExpr.split()
for token in tokenList:
if token in "0123456789":
openrandStack.push(int(token))
else:
operand2 = openrandStack.pop()
operand1 = openrandStack.pop()
result = doMath(token,operand1,operand2)
openrandStack.push(result)
return openrandStack.pop()
def doMath(op,op1,op2):
if op == "*":
return op1*op2
elif op == "/":
if op2 == 0:
return False
else:
return op1/op2
elif op == "+":
return op1+op2
elif op == "-":
return op1-op2print postfixEval('7 8 + 3 2 + /')3
队列
简介
添加新项的一端称为队尾，移除项的一端称为队首，先进先出（FIFO）
* Queue() 创建一个空的新队列。 它不需要参数，并返回一个空队列。
* enqueue(item) 将新项添加到队尾。 它需要 item 作为参数，并不返回任何内容。
* dequeue()从队首移除项。它不需要参数并返回 item。 队列被修改。
* isEmpty() 查看队列是否为空。它不需要参数，并返回布尔值。
* size()返回队列中的项数。它不需要参数，并返回一个整数。
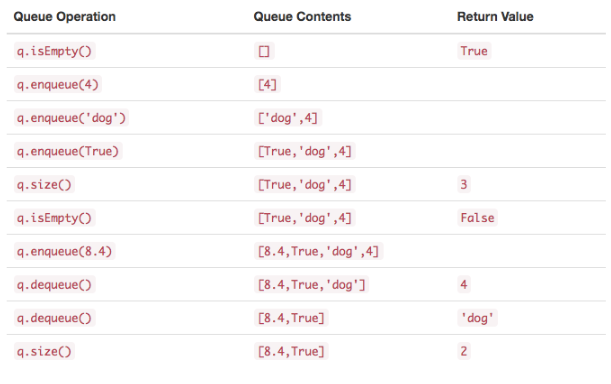
Python实现队列
假定队尾在列表中的位置为 0，入队（队尾）为 O(n)，出队为 O(1)。
class Queue():
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self,item):
self.items.insert(0,item)
def dequeue(self,item):
self.items.pop()
def size(self):
return len(self.items)q = Queue()
q.enqueue(888)
q.enqueue('11e')
print q.size()
print q.items2
['11e', 888]
模拟：烫手山芋
首先，让我们看看孩子们的游戏烫手山芋，在这个游戏中，孩子们围成一个圈，并尽可能快的将一个山芋递给旁边的孩子。在某一个时间，动作结束，有山芋的孩子从圈中移除。游戏继续开始直到剩下最后一个孩子。
from pythonds.basic.queue import Queue
def hotPotato(namelist,num):
simqueue = Queue()
for name in namelist:
simqueue.enqueue(name)
while simqueue.size()>1:
for i in range(num):
simqueue.enqueue(simqueue.dequeue())
simqueue.dequeue()
return simqueue.dequeue()
print(hotPotato(["Bill","David","Susan","Jane","Kent","Brad"],7))Susan
双端队列Deque
简介
- Deque() 创建一个空的新 deque。它不需要参数，并返回空的 deque。
- addFront(item) 将一个新项添加到 deque 的首部。它需要 item 参数 并不返回任何内容。
- addRear(item) 将一个新项添加到 deque 的尾部。它需要 item 参数并不返回任何内容。
- removeFront() 从 deque 中删除首项。它不需要参数并返回 item。deque 被修改。
- removeRear() 从 deque 中删除尾项。它不需要参数并返回 item。deque 被修改。
- isEmpty() 测试 deque 是否为空。它不需要参数，并返回布尔值。
- size() 返回 deque 中的项数。它不需要参数，并返回一个整数。
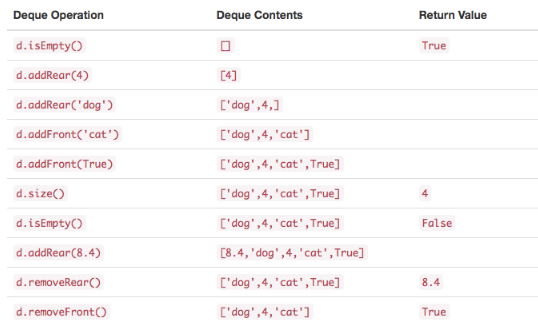
Python实现Deque
class Deque:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def addFront(self,item):
self.items.append(item)
def addRear(self,item):
self.items.insert(0,item)
def removeFront(self):
return self.items.pop()
def removeRear(self):
return self.items.pop(0)
def size(self):
return len(self.items)回文检查
如radar toot madam，我们先将字符串存入deque，如果队首队尾元素相同，删除队首队尾，直至只剩下一个字符或者0个字符
from pythonds.basic.deque import Deque
def palchecker(astring):
chardeque = Deque()
for ch in astring:
chardeque.addRear(ch)
stillEqual = True
while chardeque.size()>1 and stillEqual:
first = chardeque.removeFront()
last = chardeque.removeRear()
if first != last:
stillEqual = False
return stillEqual
print(palchecker("lsdkjfskf"))
print(palchecker("radar"))False
True
无序列表
简介
List()创建一个新的空列表。它不需要参数，并返回一个空列表。add(item)向列表中添加一个新项。它需要 item 作为参数，并不返回任何内容。假定该 item 不在列表中。remove(item)从列表中删除该项。它需要 item 作为参数并修改列表。假设项存在于列表中。search(item)搜索列表中的项目。它需要 item 作为参数，并返回一个布尔值。isEmpty()检查列表是否为空。它不需要参数，并返回布尔值。size（）返回列表中的项数。它不需要参数，并返回一个整数。append(item)将一个新项添加到列表的末尾，使其成为集合中的最后一项。它需要 item 作为参数，并不返回任何内容。假定该项不在列表中。index(item)返回项在列表中的位置。它需要 item 作为参数并返回索引。假定该项在列表中。insert(pos，item)在位置 pos 处向列表中添加一个新项。它需要 item 作为参数并不返回任何内容。假设该项不在列表中，并且有足够的现有项使其有 pos 的位置。pop()删除并返回列表中的最后一个项。假设该列表至少有一个项。pop(pos)删除并返回位置 pos 处的项。它需要 pos 作为参数并返回项。假定该项在列表中。
实现无序列表：链表
# 定义链表结点
class Node:
def __init__(self,initdata):
self.data = initdata
self.next = None
def getData(self):
return self.data
def getNext(self):
return self.next
def setData(self,newdata):
self.data = newdata
def setNext(self,newnext):
self.next = newnexttemp = Node(666)
temp.getData()666
# 定义无序链表类，只需要指出第一个结点的位置
# 空链表
class UnorderedList:
def __init__(self):
self.head = None有序列表抽象数据结构
OrderedList()创建一个新的空列表。它不需要参数，并返回一个空列表。add(item)向列表中添加一个新项。它需要 item 作为参数，并不返回任何内容。假定该 item 不在列表中。remove(item)从列表中删除该项。它需要 item 作为参数并修改列表。假设项存在于列表中。search(item)搜索列表中的项目。它需要 item 作为参数，并返回一个布尔值。isEmpty()检查列表是否为空。它不需要参数，并返回布尔值。size（）返回列表中的项数。它不需要参数，并返回一个整数。index(item)返回项在列表中的位置。它需要 item 作为参数并返回索引。假定该项在列表中。pop()删除并返回列表中的最后一个项。假设该列表至少有一个项。pop(pos)删除并返回位置 pos 处的项。它需要 pos 作为参数并返回项。假定该项在列表中。
扫一扫
4069
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
