Towards Understanding the Geometry of Knowledge Graph Embeddings理解

最新推荐文章于 2023-12-07 22:10:17 发布
最新推荐文章于 2023-12-07 22:10:17 发布
阅读量838 收藏 1
点赞数
CC 4.0 BY-SA版权
文章标签： 知识图谱
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/dreamweaverccc/article/details/88592874
该研究分析了知识图谱嵌入的几何特性，提出了ATM、Conicity和VS等度量标准。实验表明，加法模型具有低Conicity和高VS，而乘法模型则相反。此外，几何特性与模型性能的相关性在加法和乘法模型中表现不同。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

Chandrahas et al. 2018 ACL.

论文背景

知识图谱的embedding方式有多种，可按得分函数(score function)的计算表达式分为“加法模型”和“乘法模型”两类（见下图1）。本文提出新的度量指标，研究各种embedding方式的几何(geometry)性质。
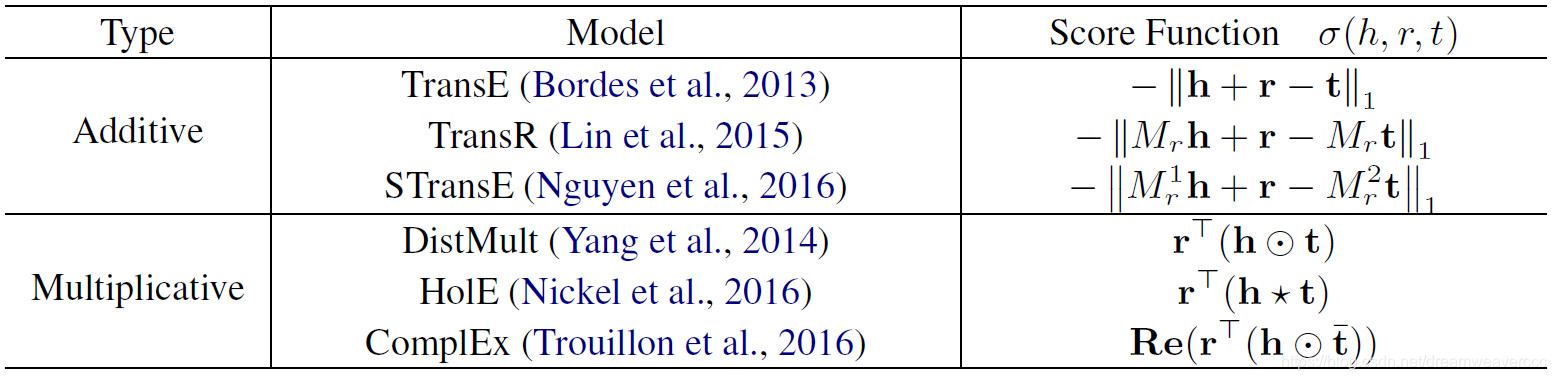
在这里插入图片描述
图1：知识图谱embedding得分函数分类

度量指标

  1. ATM(alignment to mean): the cosine similarity between vvv and the mean of all vectors in VVV. ATM(v,V)=cosine(v,1∣V∣∑x∈Vx)ATM(v, V) = cosine(v, \frac{1}{|V|}\sum_{x\in V}x)ATM(v,V)=cosine(v,∣V∣1​
最低0.47元/天 解锁文章

200万优质内容无限畅学
dreamweaverccc
关注
Towards Understanding the Geometry of Knowledge Graph Embeddings
羊城迷鹿的博客
10-04 236
研究问题 论文对知识图谱的嵌入进行了一些几何属性的研究，并指出了什么样的几何属性可以获得更好的结果，如何获得这样的几何属性 背景动机 之前已经有工作对词嵌入的几何属性进行了分析，但知识图谱领域还没有相关的研究 知识图谱分为加性、乘性和神经网络模型，不同类型的模型学习到的嵌入应该会有不同的几何属性，并进而导致有不同的表现 知识图谱需要使用负采样的方法进行训练，负采样时样本数目也会对几何属性产生影响 实验设置 模型分类 TransE、TransR、STransE为加性模型 DistMult、HolE、C
A Brief History of Word Embeddings and Their Use in NLP
AI天才研究院
08-05 966
1950年代，英文单词"word embedding"第一次出现在著名的科幻小说“狄更斯的通灵秘笈”中。当时，英语被视作计算机和语言处理领域的主要研究对象，因此，Word Embedding这一术语也被用来描述整个领域中的重要研究成果。1980年代，计算机模型如相似性匹配算法(similarity matching algorithms)或聚类算法(clustering algorithms)开始广泛使用。
CS224W摘要10.Knowledge Graph Embeddings
老毛的博客
09-27 1345
文章目录Heterogeneous Graphs and Relational GCN (RGCN)Heterogeneous GraphsRGCNblock diagonal matricesBasis/Dictionary learningLink Prediction CS224W: Machine Learning with Graphs 公式输入请参考：在线Latex公式 主要内容： 1.介绍 异质图heterogeneous graph的概念和异质图经典baseline：relational G
GNN-CS224W:10 Knowledge Graph Embeddings
u012492756的博客
03-19 312
Heterogeneous Graph 有不止一种edge、node的graph就是Heterogeneous Graph Heterogeneous Graph可以用4元组来表示：G=(V,E,R,T)G=(V,E,R,T)G=(V,E,R,T) 其中vi∈Vv_i \in Vvi​∈V表示node，node 的type可以通过T(vi)T(v_i)T(vi​)得到 edge用3元组表示(vi,r,vj)∈E(v_i, r, v_j) \in E(vi​,r,vj​)∈E，关系r∈Rr \in Rr∈R
9-Knowledge Graph Embeddings
m0_50976935的博客
09-23 434
G=(V,E,R,T)，分别代表节点，边，边类型，节点类型。
cs224w-图机器学习-2021冬季课程学习笔记-10 Knowledge Graph Embeddings
weixin_43963453的博客
08-28 1180
Knowledge Graph Embeddings一、 Heterogeneous Graphs and Relational GCN (RGCN)1.Heterogeneous Graphs and Relational GCN (RGCN)2.Relational GCN（1） block diagonal matrices（2）basis learning3.RGCN链路预测应用（1）验证集、训练集的划分（2）边的得分函数（3）负采样的方法（4）训练流程（5）验证、测试阶段二、 Knowledge
2020年NLP所有领域最新、经典、顶会、必读论文
lqfarmer的博客
05-23 5235
本资源整理了近几年，自然语言处理领域各大AI相关的顶会中，一些经典、最新、必读的论文，涉及NLP领域相关的，Bert模型、Transformer模型、迁移学习、文本摘要、情感分析、问答、机器翻译、文本生成、质量评估、纠错(多任务、masking策略等。)、Probe、多语言、领域相关、多模态、模型压缩、谓词填充、Analysis、分词解析NER、代词指代消解、词义消歧、情感分析、关系抽取、知识库、文本分类等，几乎所有领域。 资源整理自网络，源地址：https://github.com/...
AI4S - 结构生物学中的机器学习 (NIPS MLSB Workshop) 教程
AGI
07-04 486
结构生物学是对于蛋白质和其他生物分子 3D 结构或形状的研究，机器学习算法的突破已经改变了结构生物学。
cs224w（图机器学习）2021冬季课程学习笔记12 Knowledge Graph Embeddings
诸神缄默不语的博客
07-07 4292
cs224w（图机器学习）2021冬季课程学习笔记12 Knowledge Graph Embeddings 1. Heterogeneous Graphs and Relational GCN (RGCN) 2. Knowledge Graphs: KG Completion with Embeddings 3. Knowledge Graph Completion: TransE, TransR, DistMult, ComplEx
KnowledgeGraphEmbeddingsViaPairedRelationVectors_PairRE
05-24
PairRE 纸代码。 这对于PairRE实施数据集（ogbl-wikikg和ogbl-biokg）是基于 。 感谢您的贡献。 设置 要运行代码，您需要以下依赖项： 结果 PairRE在ogbl-wikikg ， ogbl-biokg和ogbl-wikikg2上的结果如下。 ogbl-wikikg ＃暗淡 ＃参数 硬件 测试MRR 有效的MRR PairRE 100 250,167,400 16GB GPU 0.4912±0.004 0.5013±0.004 PairRE 200 500,334,800 16GB GPU 0.5289±0.003 0.5529±0.001 生物蛋白 ＃暗淡 ＃参数 硬件 测试MRR 有效的MRR PairRE 2000 187,750,000 16GB GPU 0.8164±0.0005 0.8172±0.
Iteratively Learning Embeddings and Rules for Knowledge Graph Reasoning.pdf
08-09
Reasoning is essential for the development of large knowledge graphs,especiallyforcompletion,whichaimstoinfernewtriples basedonexistingones.Bothrulesandembeddingscanbeusedfor knowledgegraphreasoningandtheyhavetheirownadvantages anddifficulties.Rule-basedreasoningisaccurateandexplainable butrulelearningwithsearchingoverthegraphalwayssuffersfrom efficiencyduetohugesearchspace.Embedding-basedreasoningis morescalableandefficientasthereasoningisconductedviacomputationbetweenembeddings,butithasdifficultylearninggood representationsforsparseentitiesbecauseagoodembeddingrelies heavilyondatarichness.Basedonthisobservation,inthispaper we explore how embedding and rule learning can be combined together and complement each other’s difficulties with their advantages.WeproposeanovelframeworkIterEiterativelylearning embeddingsandrules,inwhichrulesarelearnedfromembeddings with proper pruning strategy and embeddings are learned from existingtriplesandnewtriplesinferredbyrules.Evaluationson embeddingqualitiesofIterEshowthatruleshelpimprovethequality of sparse entity embeddings and their link prediction results. Wealsoevaluatetheefficiencyofrulelearningandqualityofrules fromIterEcomparedwithAMIE+,showingthatIterEiscapableof generatinghighqualityrulesmoreefficiently.
Knowledge_Graph_Reasoning_Papers:必读的知识图推理论文
04-29
知识图推理论文 主要由，并维护。 感谢GitHub上所有杰出的贡献者！ 内容 4.1基于路径的查询 4.2复杂逻辑查询 4.3复杂自然语言查询 5.基准与评估 致谢 1.调查文件 评论：知识图上的知识推理。 陈晓军，贾胜斌，杨翔。 具有应用程序的专家系统。 纸 2.多跳推理 2.1实体预测 预测丢失的尾部实体和相应的支撑路径为三分之一。 （h，r，？）->（h，r，t） 散步并到达答案：使用强化学习对知识库中的路径进行推理。 拉贾尔·达斯（Rajarshi Das），谢赫扎德·杜利亚瓦拉（Shehzaad Dhuliawala），曼齐尔·扎海尔（Manzil Zaheer），卢克·维尔尼斯（Luke Vilnis），伊桑·杜鲁格卡（Ishan Durugkar），阿克舍·克里希那穆提（Alexs Smola），安德鲁·麦卡勒姆（Andrew McCallum）。 ICLR 20
知识图谱经典方法 Knowledge Graph Embedding：从TransE，TransH到TransR
给我也整一个
11-05 6625
1.背景 KG Embedding可以建立实体到实体的关联。
DisenE: Disentangling Knowledge Graph Embeddings
qq_42397330的博客
01-30 442
解耦知识图谱嵌入 创新点：本文利用注意力机制将实体的表示分解为了多个部分 1 动机 以往对知识图谱嵌入的研究，通常是基于黑盒模型的，这导致很难对学习到的表示进行解释 于是本文引入注意力机制，根据实体之间的关系，使模型显式集中在实体嵌入的几个component(我将其称为组成部分)，简单来说，学习的实体表示可以解耦为多个向量 2 举例 实体 “David Beckham” 可能包括几个组成部分，例如，“Characteristic”、“Work”、“Family”、"Places"等 对于关系
简单实现几篇知识图谱嵌入(Knowledge Graph Embedding，KGE)模型
热门推荐
xhsun的博客
11-07 1万+
两个问题 KGE可以用来做什么？ KGE的诸多方法？ 下面来聊聊上面提出的两个问题 KGE可以用来做什么？ 知识图谱KG，特别是开放域知识图谱，一定是不完整的，因为不可能穷举所有实体，而实体之间的各种关系也不可能都一一存在。 连接预测(link prediction)任务，也叫知识图谱补全。就是利用当前KG中的实体和关系去推理出新的实体或者关系。 比如给定(h,r,?)，其中h是头实体，r是关系，我们想知道尾实体是什么。或者给定(h,?,t)，想知道r是什么。这就是连接预测任务，目的是补全知识图谱。 有
阅读文章：Incorporating Knowledge Graph Embeddings into Topic Modeling
smileyk的专栏
10-13 1246
阅读文章：Incorporating Knowledge Graph Embeddings into Topic Modeling这是一篇发表到AAAI-17的Oral的文章：Incorporating Knowledge Graph Embeddings into Topic ModelingIntroduction：主体模型PLSA或者LDA作为无监督模型，若没有人类领域知识的帮助，得到的主题经
Learning Entity and Relation Embeddings for Knowledge Graph Completion (TransR)论文翻译
鲁鲁晓生
03-28 3358
整理转自：fffnull 的 优快云 博客，感谢他的翻译分享 论文原文地址：Learning Entity and Relation Embeddings for Knowledge Graph Completion
【论文笔记】Interaction embeddings for prediction and explanation in knowledge graphs
weixin_40530554的博客
04-13 666
摘要 交叉交互——实体和关系之间的双向效应——有助于在预测新的三元组时选择相关信息，但之前还没有正式讨论过。 本文提出了CrossE，它明确地模拟交叉交互。它不仅像大多数以前的方法一样，为每个实体和关系学习一个一般的嵌入，而且还为实体和关系生成多个特定的三重嵌入，称为交叉嵌入。 此外，我们从一个新的角度评估嵌入——解释预测的三元组。在这项工作中，三元组的解释被认为是头部和尾部实体之间可靠的闭合路径。 背景 关系到实体的交互：一个实体构成很多三元组，但只有部分三元组对于某种关系的预测起到作用。比如对于X是谁的
【论文合集】在非欧空间中的图嵌入方法（Graph Embedding in Non-Euclidean Space）
最新发布
开着奔驰种地的博客
12-07 1268
在非欧空间中的图嵌入方法（Graph Embedding in Non-Euclidean Space），分为 Hyperbolic Models，Spherical models 和 Gaussian models三类
Towards Generalizable Neural Networks for Graph Applications发表在哪里
06-12
该论文 "Towards Generalizable Neural Networks for Graph Applications" 发表在2020年的国际顶级人工智能会议NeurIPS (The Conference on Neural Information Processing Systems)上。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值