算法价值6-梯度下降

梯度下降算法(gradient descent algorithm)是一种常用的优化算法，用于寻找函数的最小值点或最小化损失函数。它的核心思想是通过迭代调整参数的值，使目标函数的值逐渐趋于最小值。

 

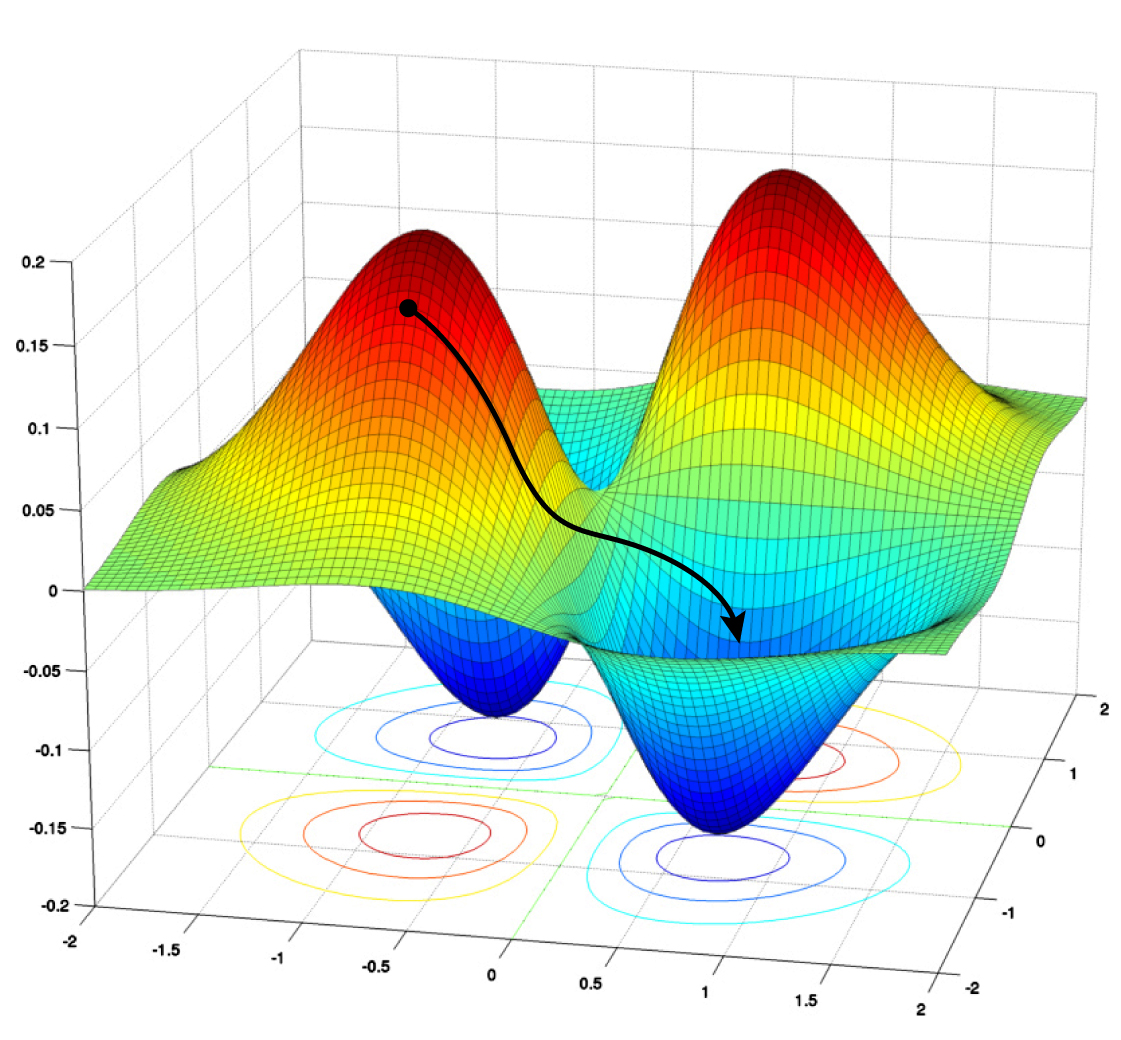
具体来说，梯度下降算法的步骤如下：

1. 初始化参数

首先，需要初始化待优化的参数，可以随机初始化或者根据经验值来设定初始值。

2. 计算损失函数的梯度

接下来，计算损失函数关于每个参数的梯度（偏导数）。梯度表示了损失函数在当前参数值处的变化率，即函数变化最快的方向。

3. 更新参数

根据梯度的方向和大小来更新参数的值。通过在当前参数值上减去学习率乘以梯度，可以沿着梯度的反方向移动一小步，从而使损失函数的值减小。

4. 重复迭代

重复执行步骤 2 和步骤 3，直到达到停止迭代的条件。通常的停止条件可以是达到最大迭代次数、损失函数的变化小于某个阈值，或者梯度的大小小于某个阈值。

梯度下降算法有不同的变种，包括批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-batch Gradient Descent）。这些变种的区别主要在于每次更新参数时所使用的样本数量不同，但核心思想都是相似的：沿着损失函数的梯度方向调整参数的值，以逐