笔试强训：Week-1

1.数字统计（数字+模拟）

数字统计_牛客题霸_牛客网

枚举，通过%10 /10操作，得到每一位的数

#include <iostream>
using namespace std;
int l,r;
int main() {
   cin>>l>>r;
   int ret=0;
   for(int i=l;i<=r;++i){
    int tmp=i;
    while(tmp){
        ret+=tmp%10==2;
        tmp/=10;
    }
   }
   cout<<ret<<endl;
}
// 64 位输出请用 printf("%lld")

2.两个数组的交集（哈希/双指针）

两个数组的交集_牛客题霸_牛客网

解法一：哈希，遍历第一个数组，将数据存进哈希表，遍历第二个数组的时候看一下数据有没有存过就行，存过加入我们的ret数组，同时更新这个元素的哈希值

class Solution {
public:
    bool hash[1010]={0};
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
       vector<int> ret;
       for(auto&e:nums1) hash[e]=true;
       for(auto&e:nums2) 
          if(hash[e]){
            ret.emplace_back(e);
            hash[e]=false;
          }
       return ret;
    }
};

解法二：双指针，先排序两个数组，创建两个指针从两个数组开头开始遍历，比较所指元素大小，小的那个++，相等就加入ret数组

class Solution {
  public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        int cur1 = 0, cur2 = 0;
        vector<int> ret;
        while (cur1 < nums1.size() && cur2 < nums2.size()) {
            if (nums1[cur1] < nums2[cur2])++cur1;
            else if (nums2[cur2] < nums1[cur1])++cur2;
            else {
                if (ret.empty() || nums1[cur1] != ret.back())ret.push_back(nums1[cur1]);
                ++cur1;
                ++cur2;
            }
        }
        return ret;
    }
};

3.点击消除（模拟+栈）

点击消除_牛客题霸_牛客网

因为需要消除相邻的相等元素，删除完一次可能又会使两个相同的元素相邻，消除相邻的元素就可以利用栈的思路，创建一个字符串ret模拟栈的行为，如果ret是空的或者ret的末尾不等于遍历到的元素，加入字符串，否则就pop_back

#include <iostream>
#include <stack>
#include <string>
using namespace std;
 
int main() {
    string s,st;
    cin>>s;
    for(auto&ch:s)
      if(st.empty()||st.back()!=ch) st+=ch;
      else st.pop_back();
   cout << (st.empty()?"0":st) << endl;
 
}
// 64 位输出请用 printf("%lld")

4*.牛牛的快递（模拟）

牛牛的快递_牛客题霸_牛客网

拓展两个库函数：ceil（向上取整） 和 floor（向下取整）#include<cmath>

#include <iostream>
#include <cmath>
using namespace std;
 
int main() {
    float a;//重量
    char b;//是否加急
    cin>>a>>b;
    int ret=20;//无论如何都至少有20
    if(a>1)  ret+=ceil(a-1);//向上取整
    if(b=='y') ret+=5;
    cout<<ret<<endl;
}
// 64 位输出请用 printf("%lld")

5.最小花费爬楼梯（线性dp）

最小花费爬楼梯_牛客题霸_牛客网

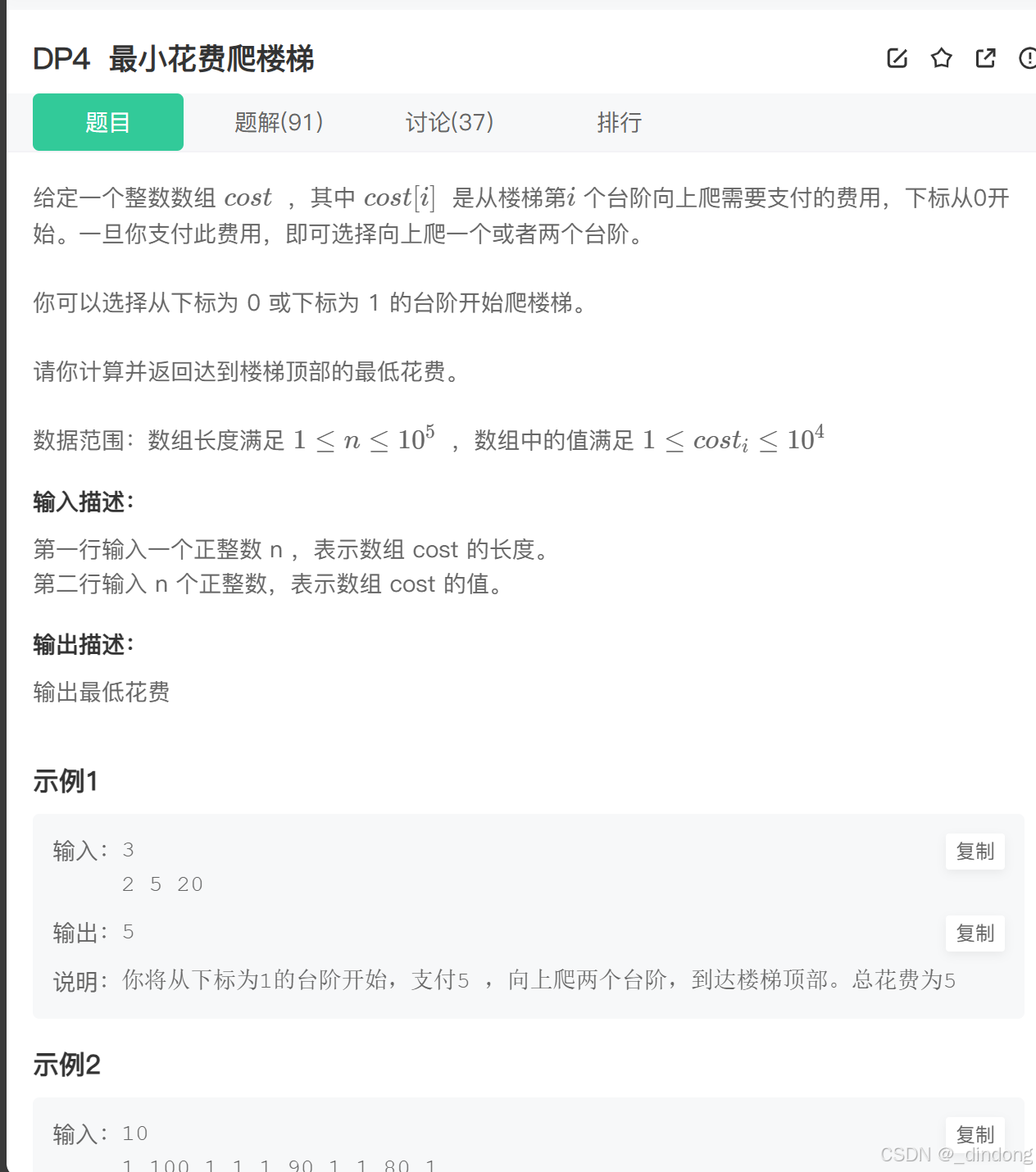
爬到下标为n的位置才是爬完，不是n-1

状态转移方程很简单

#include <iostream>
using namespace std;
const int N=1e5+1;
int dp[N];
int cost[N];
int main() {
    //dp[i]表示以i位置结尾时 所需要的最小花费
    int n;
    cin>>n;
    for(int i=0;i<n;++i) cin>>cost[i];//记录上花费
    for(int i=2;i<=n;++i) 
        dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
    cout<<dp[n]<<endl;
}
// 64 位输出请用 printf("%lld")

6.数组中两个字符串的最小距离（贪心）

数组中两个字符串的最小距离__牛客网

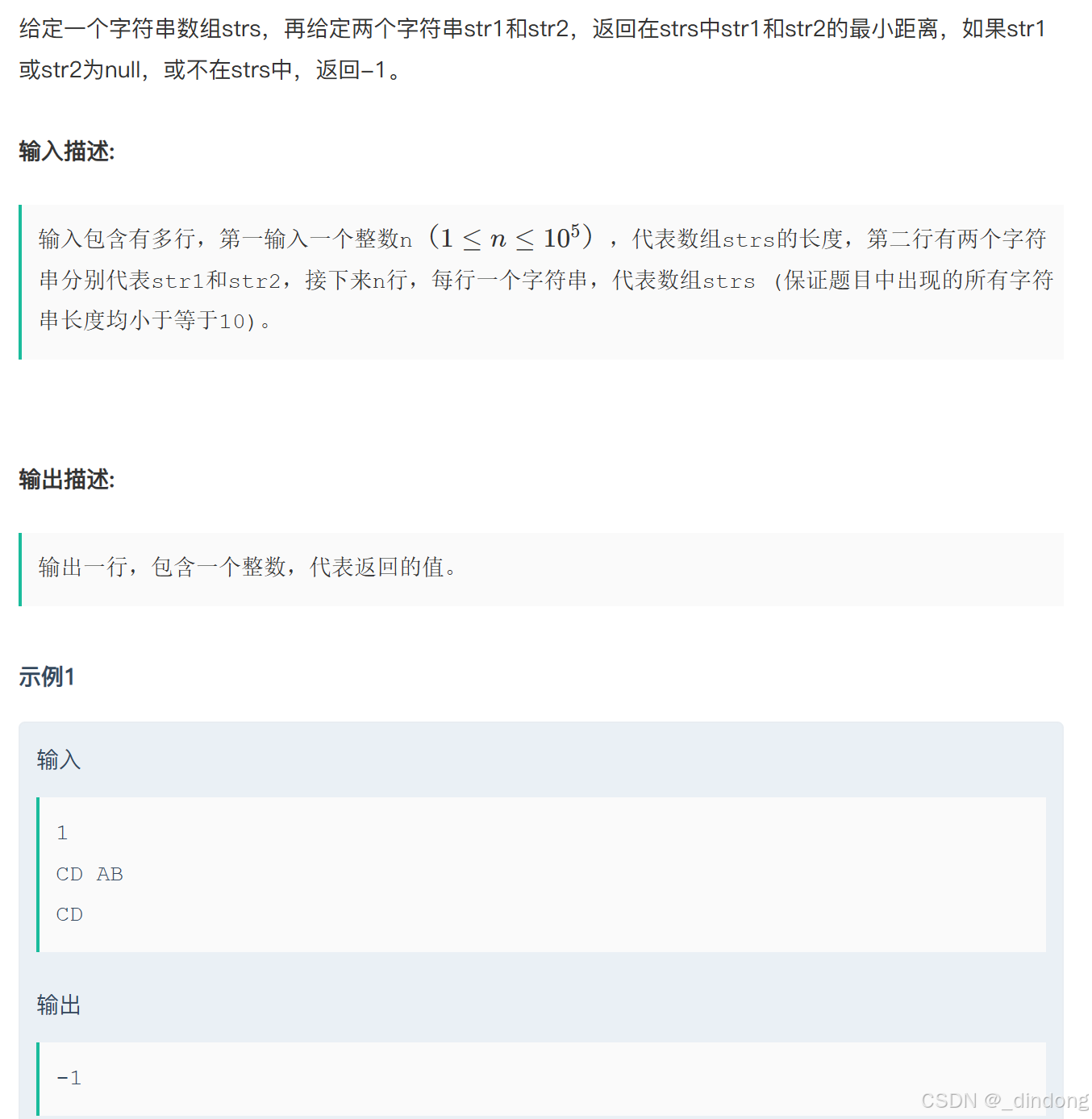
prev1标记上一次出现的第一个字符串的下标

prev2标记上一次出现的第二个字符串的下标

0x3f3f3f3f是一个很大的数

#include <iostream>
#include<string>
using namespace std;
 
int main() {
    int n;
    string str1,str2;
    cin>>n>>str1>>str2;
    string s;
    int prev1=-1,prev2=-1,ret=0x3f3f3f3f;
    for(int i=0;i<n;++i){
        cin>>s;
        //因为我们要找的是最近的 所以我们只要保留尽量靠后的下标就行了
        if(s==str1){//当找到相同的时候
            if(prev2!=-1) ret=min(ret,i-prev2);
            prev1=i;
        }
        else if(s==str2){
            if(prev1!=-1) ret=min(ret,i-prev1);
            prev2=i;
        }
    }
    if(ret==0x3f3f3f3f) cout<<-1<<endl;
    else cout<<ret<<endl;
}
// 64 位输出请用 printf("%lld")

7*.简写单词（模拟）

简写单词_牛客题霸_牛客网

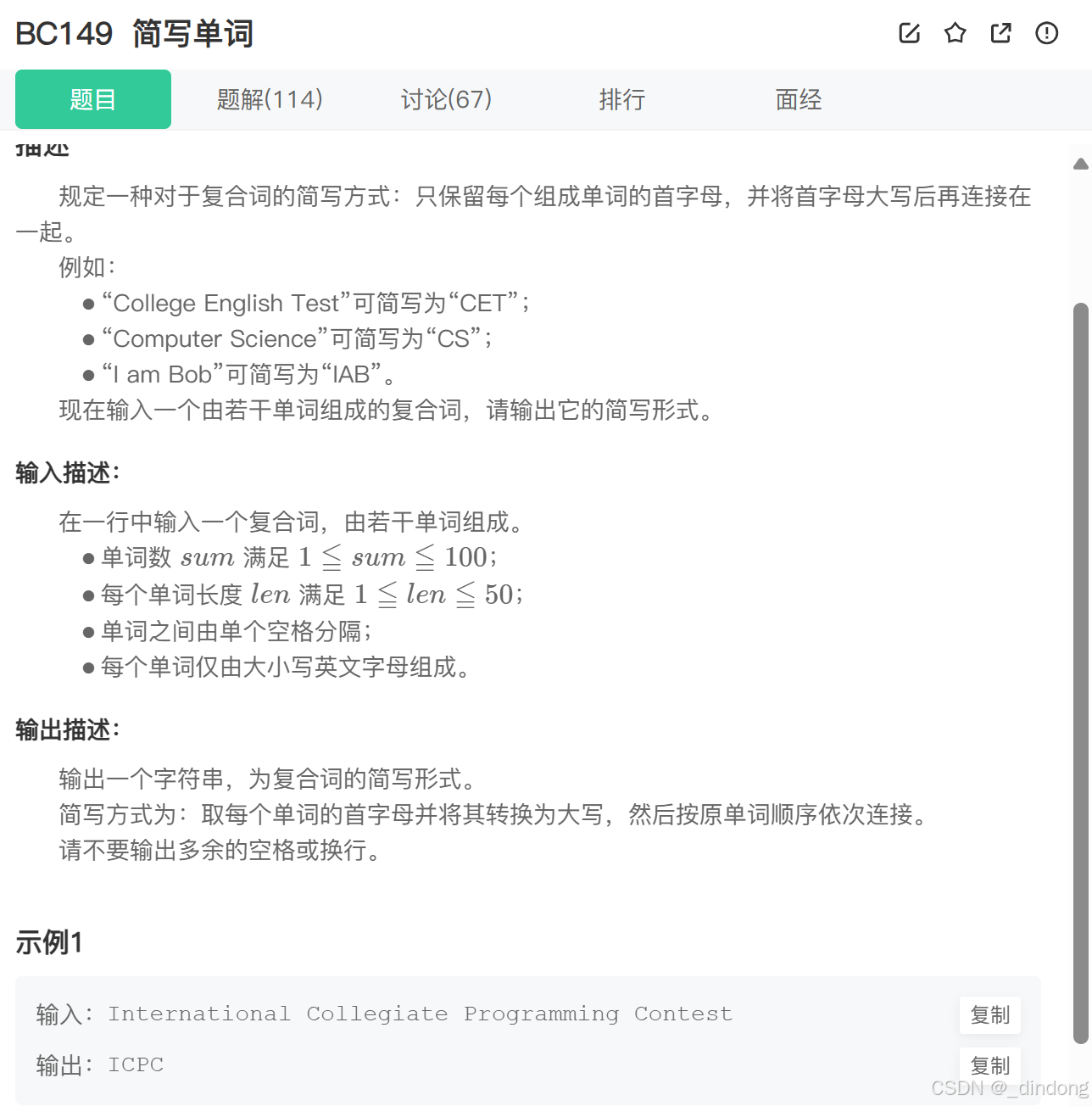
简单模拟题，主要是处理输入问题。通过while(cin>>s)可以帮助我们跳过空格

#include <cctype>
#include <iostream>
#include <string>
using namespace std;
//cctype头文件  0-9 isdigit a-z islower A-Z isupper 字母isalpha 字母+数字isalnum
int main() {
   string s;
   while(cin>>s){//可以自动跳过空格  
     if(islower(s[0])) s[0]-=32;//-=32是小写转大写 ^=是大小写互换
     cout<<s[0];
   }
   return 0;
}
// 64 位输出请用 printf("%lld")

#include<cctype>

0~9 isdigit

a~z islower

A~Z isupper

字母 isalpha

字母+数字 isalnum

转大写 toupper

转小写 tolower

大小写转换 ^=32，因为大小写字母相差32，也就是只有二进制第6位不一样

8*.dd爱框框（滑动窗口）

dd爱框框

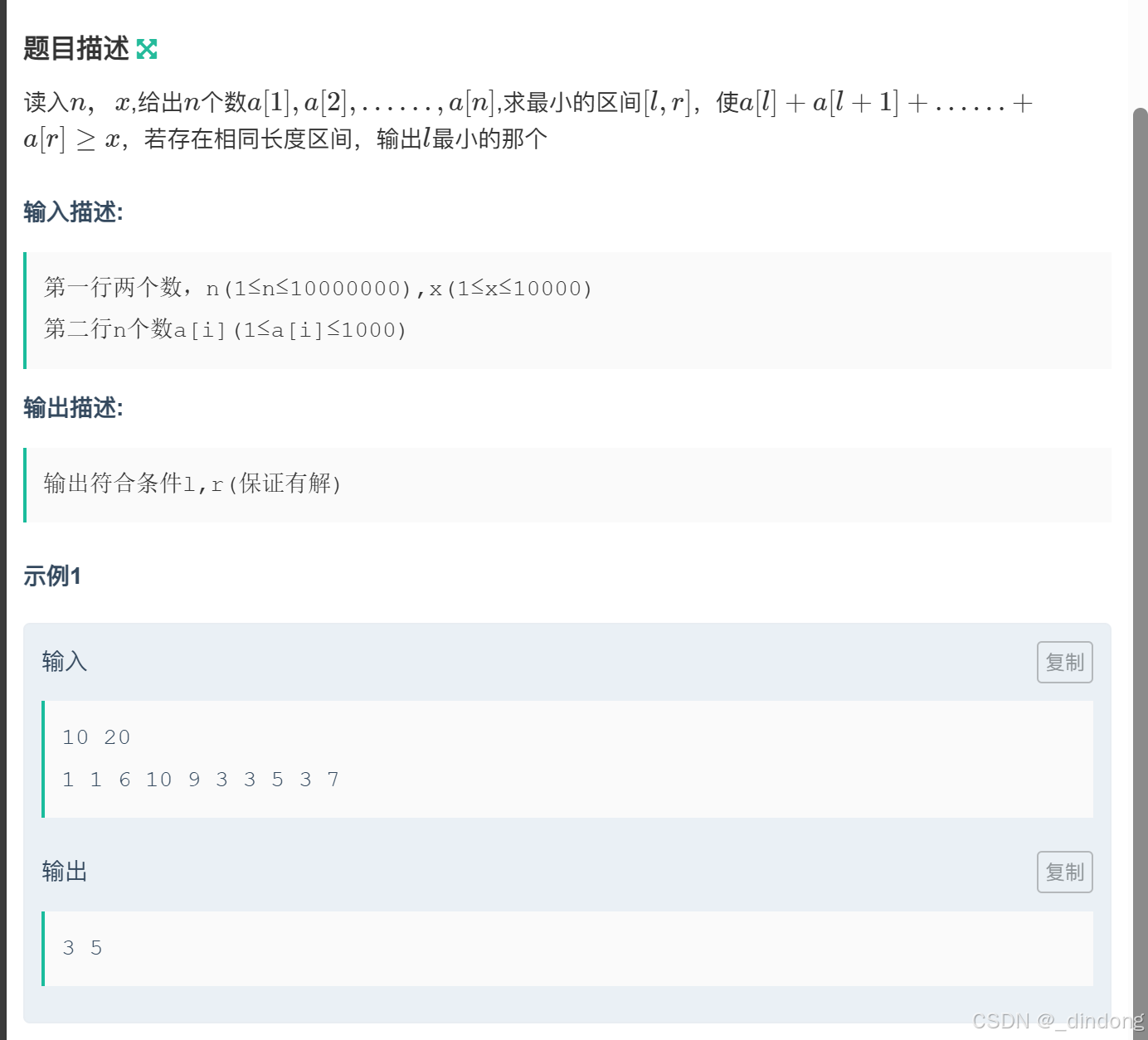
数组可以用全局数组，提前设置一个常量const int N=1e+7;

#include<iostream>
const int N=1e7+1;
int nums[N];
using namespace std;
int main(){
    int n,x;
    cin>>n>>x;   
    //本题下标从1开始
    for(int i=1;i<=n;++i) cin>>nums[i];
    int l=-1,r=n;    //存储符合的区间，在滑动的时候更新
    int sum=0;
    for(int left=1,right=1;right<=n;++right){
        //right滑入窗口
        sum+=nums[right];
        //注意是while
        while(sum>=x){
            if(right-left<r-l) l=left,r=right;      //判断是否更新
            sum-=nums[left++];    //left滑出窗口
        }
    }
    cout<<l<<" "<<r;
    return 0; 
}

9*.除2！（贪心+优先级队列）

除2！

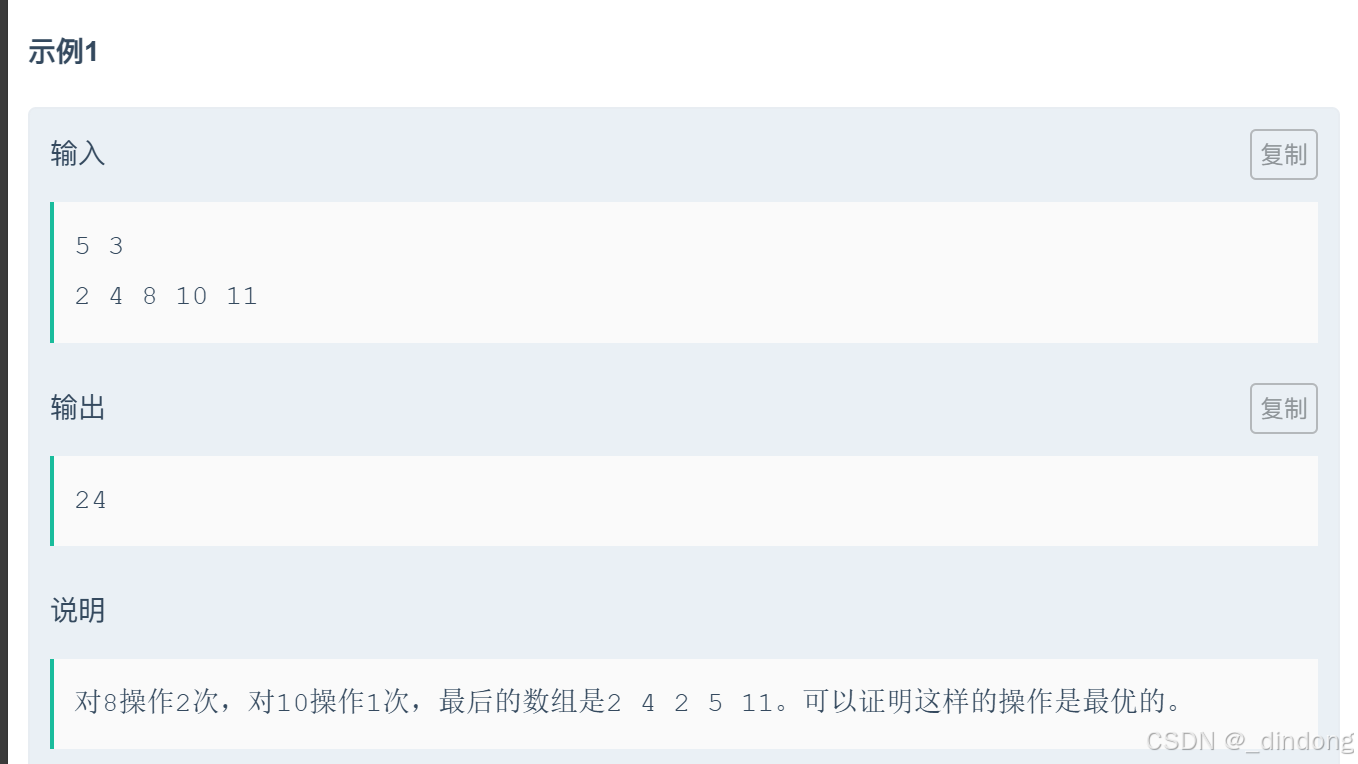
思路：创建默认的优先级队列，把偶数存进来，每次取堆顶元素除以2，删堆顶，如果除以2之后是偶数还需要再次加入优先级队列。

c++中，优先级队列中less（默认是less）和greater表示趋势，优先级队列相比之下看重的是一种未来的趋势（注意这里是我胡扯，方便记忆而已），less递减，greater递增，所以默认创建大根堆。

set和map则表现得“低级”一些，它只看重当下最前面的数值，less表示小的放前面，greater表示大的放前面，所以是less递增，greater递减

//用一个堆模拟一下  该题数据量很大，所以可以用long
//但是最好还是不要用long 因为有的平台下他也是4个字节
#include<iostream>
#include<queue>//优先级队列是在这个头文件里面的
using namespace std;
typedef long long LL;//对类型重命名，这样方便写
int main(){
    int n,k;
    cin>>n>>k;
    LL x,sum;//一个用来统计数据，一个用来计算总和
    priority_queue<LL> q;
    while(n--){//如果这个变量无所谓变化的话,其实用while比for循环会更简洁一点
        cin>>x;
        sum+=x;
        if(x%2==0) q.push(x);
    }
   while(!q.empty()&&k--){
        x=q.top()/2;q.pop();
        sum-=x;
        if(x%2==0) q.push(x);
    }
    cout<<sum;
    return 0;
}

10.Fibonacci数列（动规斐波那契/递推）

Fibonacci数列_牛客题霸_牛客网

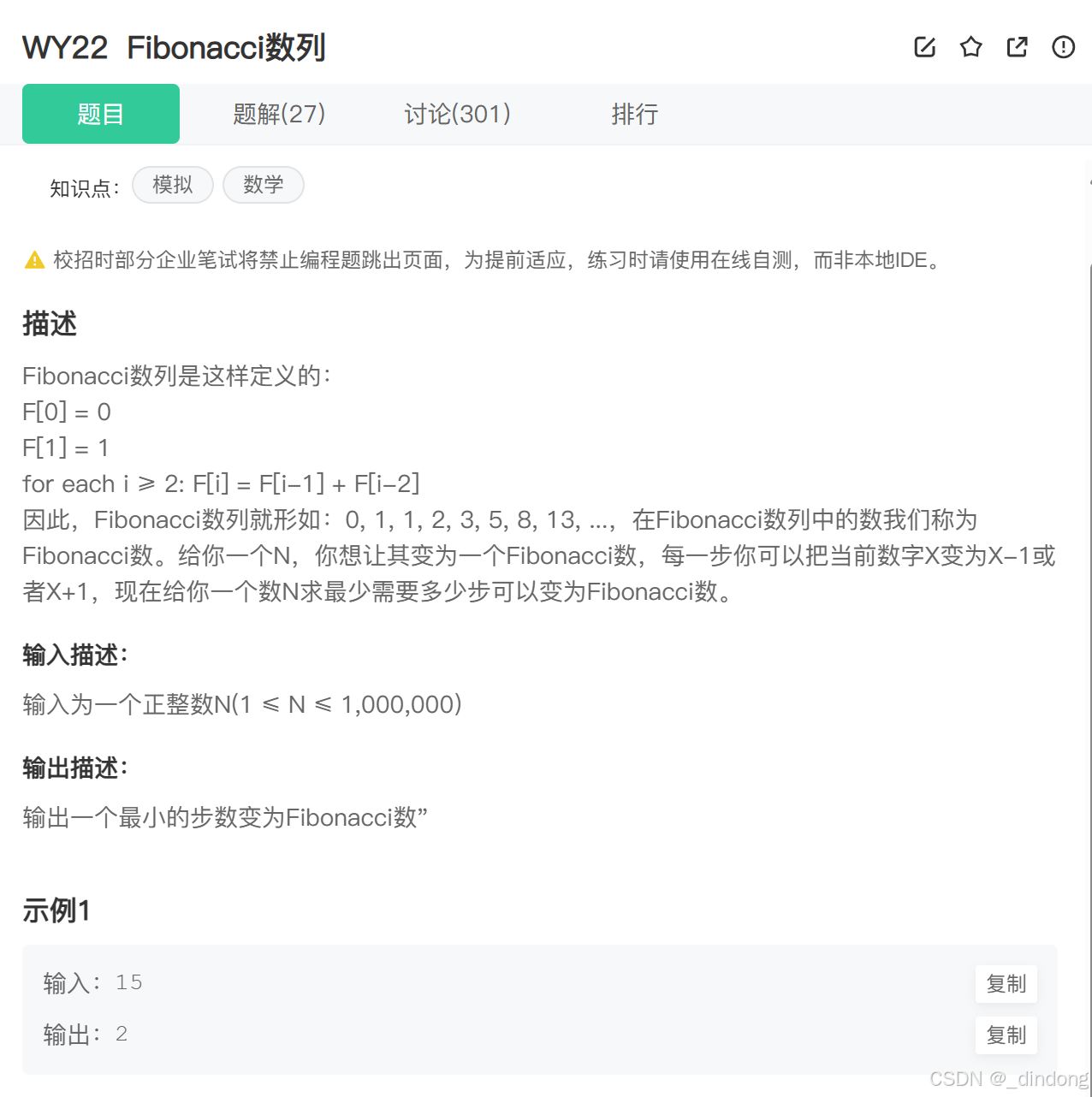
可以让三个变量递推，一直到最大的那个变量大于n结束，此时也保存了第二大的变量，只需判断一下 第二大的变量到n 和 n到最大的变量的最小值。

#include <iostream>
using namespace std;
int main() {
    int n;
    cin>>n;
    int a=0,b=1,c=1;
    while(n>c){
        a=b;
        b=c;
        c=a+b;
    }
    cout<<min(c-n,n-b);
    return 0;
}
// 64 位输出请用 printf("%lld")

11*.单词搜索（dfs）

单词搜索_牛客题霸_牛客网

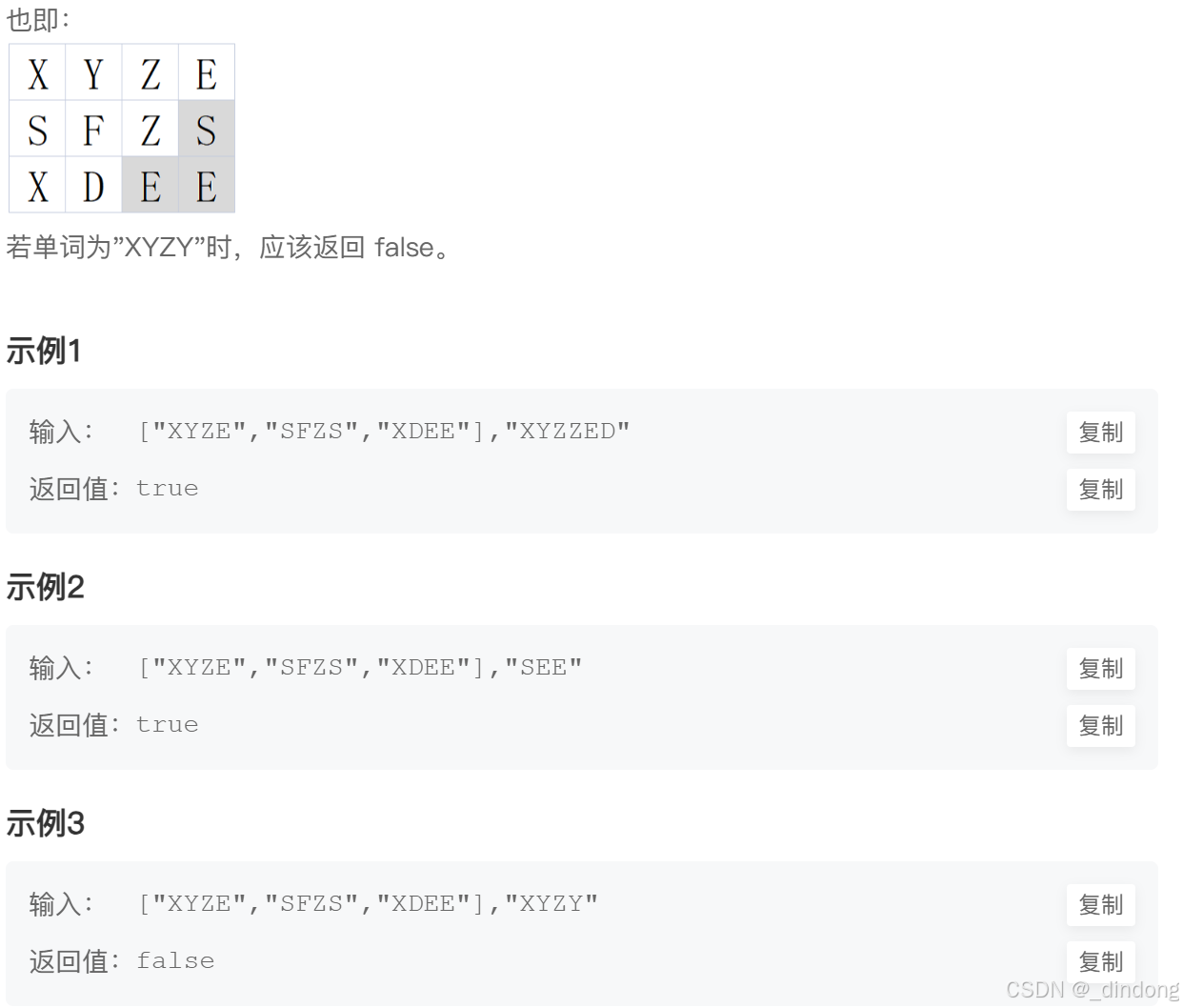
简单的dfs

注意四个地方

1.创建一个标记数组避免重复

2.dfs也是判断条件，而不是当作if判断符合后的内部语句return

3.不符合时需要将原先标记的标记数组置回原来的，return如果是一个赋值，则返回赋值后的这个变量

4.pos==size-1才符合，不是pos==size，不然pos+1会越界（访问size）

class Solution {
public:
//dfs专题
int m,n;
bool vis[101][101];//标记数组
int dx[4]={0,0,1,-1};//向量数组
int dy[4]={1,-1,0,0};
    bool exist(vector<string>& board, string word) {
        m=board.size(),n=board[0].size();
        for(int i=0;i<m;++i)
           for(int j=0;j<n;++j)
              if(board[i][j]==word[0]&&dfs(board,i,j,word,0)) return true;
        return false;   
    }
    bool dfs(vector<string>& board,int i,int j,string&word,int pos){
        if(pos==word.size()-1) return true;
        vis[i][j]=true;
        for(int k=0;k<4;++k){
            int x=dx[k]+i,y=dy[k]+j;
            if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]
            &&board[x][y]==word[pos+1]
            &&dfs(board,x,y,word,pos+1)) return true;
        }
        return vis[i][j]=false;
    }
};

12.杨辉三角（线性dp）

杨辉三角_牛客题霸_牛客网

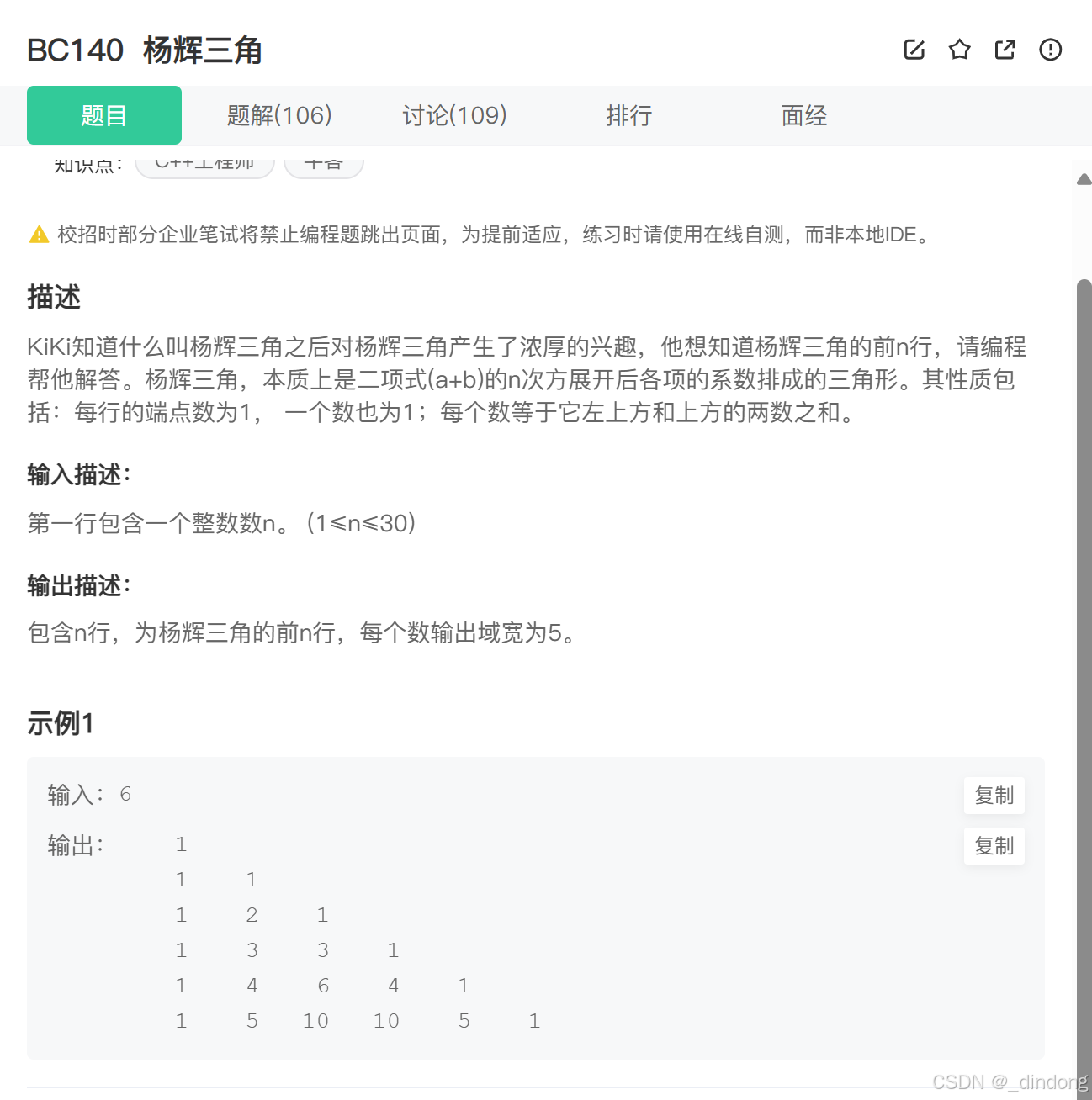
多创建一行一列虚拟边界，方便填表，不要忘记函数数组内部要初始化为0

#include <iostream>
using namespace std;
int dp[31][31];//一层虚拟边界
int main() {
    int n;
    cin>>n;
    dp[1][1]=1;
    for(int i=2;i<=n;++i)
      for(int j=1;j<=i;++j) 
        dp[i][j]=dp[i-1][j]+dp[i-1][j-1];
    //开始打印 要按照输出格式
    for(int i=1;i<=n;++i){
      for(int j=1;j<=i;++j)
         printf("%5d",dp[i][j]);
      printf("\n");
    }        
    return 0;
}
// 64 位输出请用 printf("%lld")

13.游游的you（贪心+模拟）

游游的you__牛客网

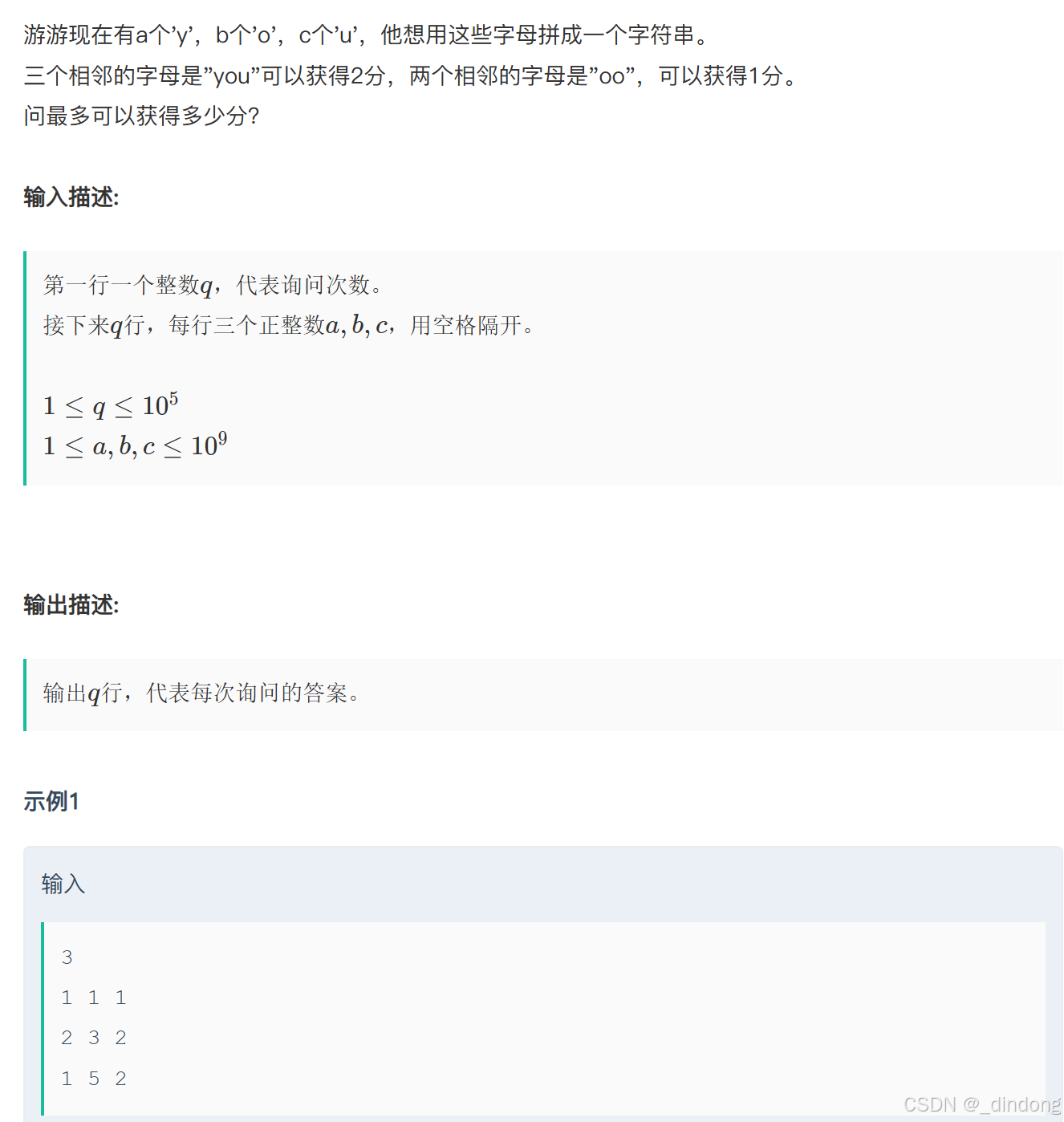
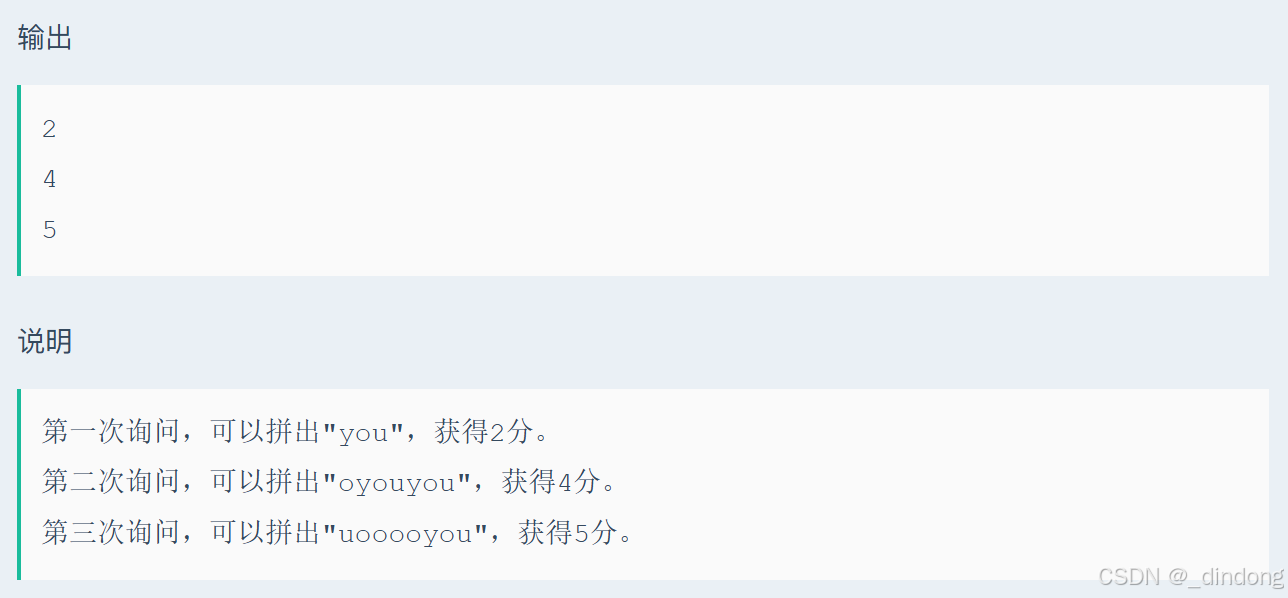
优先凑you，然后后续就是剩下的o的数量减去1，就是能拼成的oo数量，但是剩下的o的数量要判断是不是大于1，如果只剩下一个也无法拼成

#include <iostream>
using namespace std;
//贪心策略 最好的情况下我们拼出尽可能多的you  然后剩下的拼oo
//oo是第一个不算 剩下的连在一起的可以算
int main() {
    int q,a,b,c;//q是询问次数 a b c是you分别的个数
    cin>>q;
    while(q--){
        cin>>a>>b>>c;
        int x=min(a,min(b,c));//最小值决定了可以有几个you
        cout<<(x*2+max((b-x-1),0))<<endl;
    }
}
// 64 位输出请用 printf("%lld")

14*.腐烂的苹果（多源bfs）

腐烂的苹果_牛客题霸_牛客网

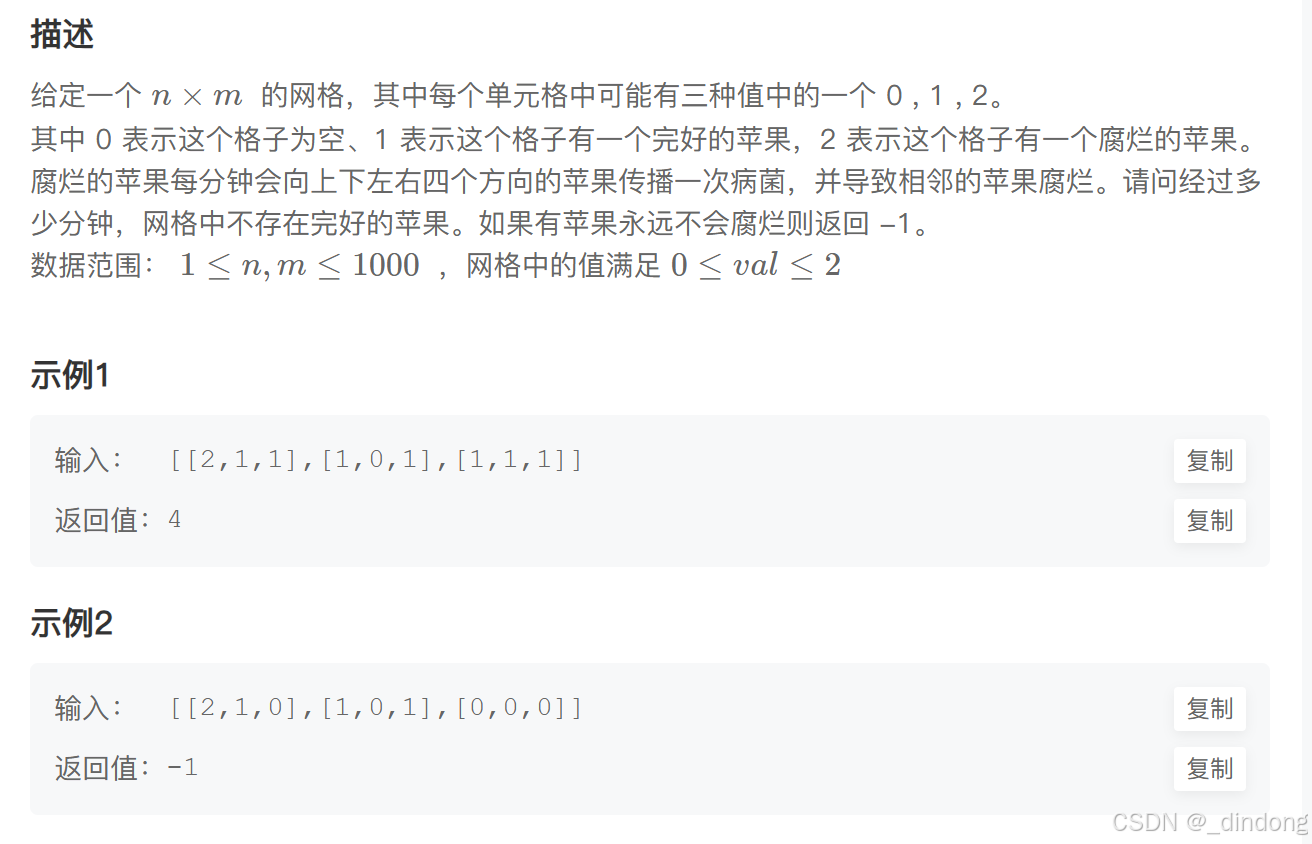
#include <queue>
class Solution {
public:
    int dx[4]={0,0,-1,1};
    int dy[4]={1,-1,0,0};
    int rotApple(vector<vector<int> >& grid) {
       int m=grid.size(),n=grid[0].size();
       queue<pair<int,int>> q;
       for(int i=0;i<m;++i)
         for(int j=0;j<n;++j)
            if(grid[i][j]==2)  q.emplace(i,j);
       int ret=0;//统计时间
       while(!q.empty()){
          ++ret;
          //定义最好用sz，可能会不小心写成n和原数组的n冲突
          int sz=q.size();
          for(int i=0;i<sz;++i){
            auto [a,b]=q.front();
            q.pop();
            for(int k=0;k<4;++k){
                int x=dx[k]+a,y=dy[k]+b;
                if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]==1){
                    q.emplace(x,y);
                    grid[x][y]=2;
                }
            }
          }
       }
       //这个时候已经扩散完了 还需要去检查一下有没有完好的苹果
       for(auto&v:grid) 
         for(auto&e:v)
           if(e==1) return -1;
        //注意是返回ret-1，因为感染到最后一个苹果就结束了，此时不用再往下了但还要遍历一层删掉元素while才退出
       return ret-1;
    }
};

15*.孩子们的游戏（循环链表/dp+数学）

孩子们的游戏(圆圈中最后剩下的数)_牛客题霸_牛客网

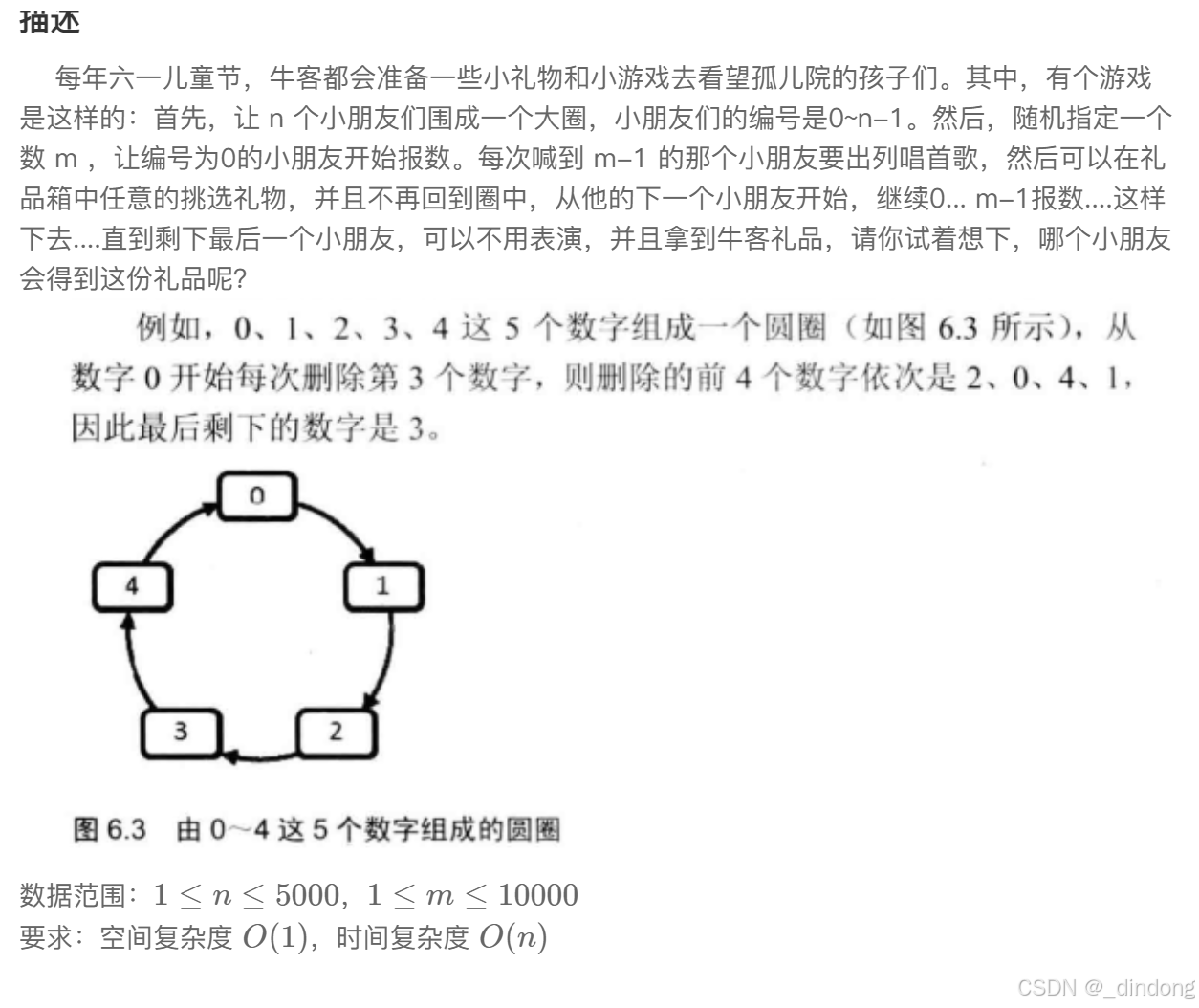
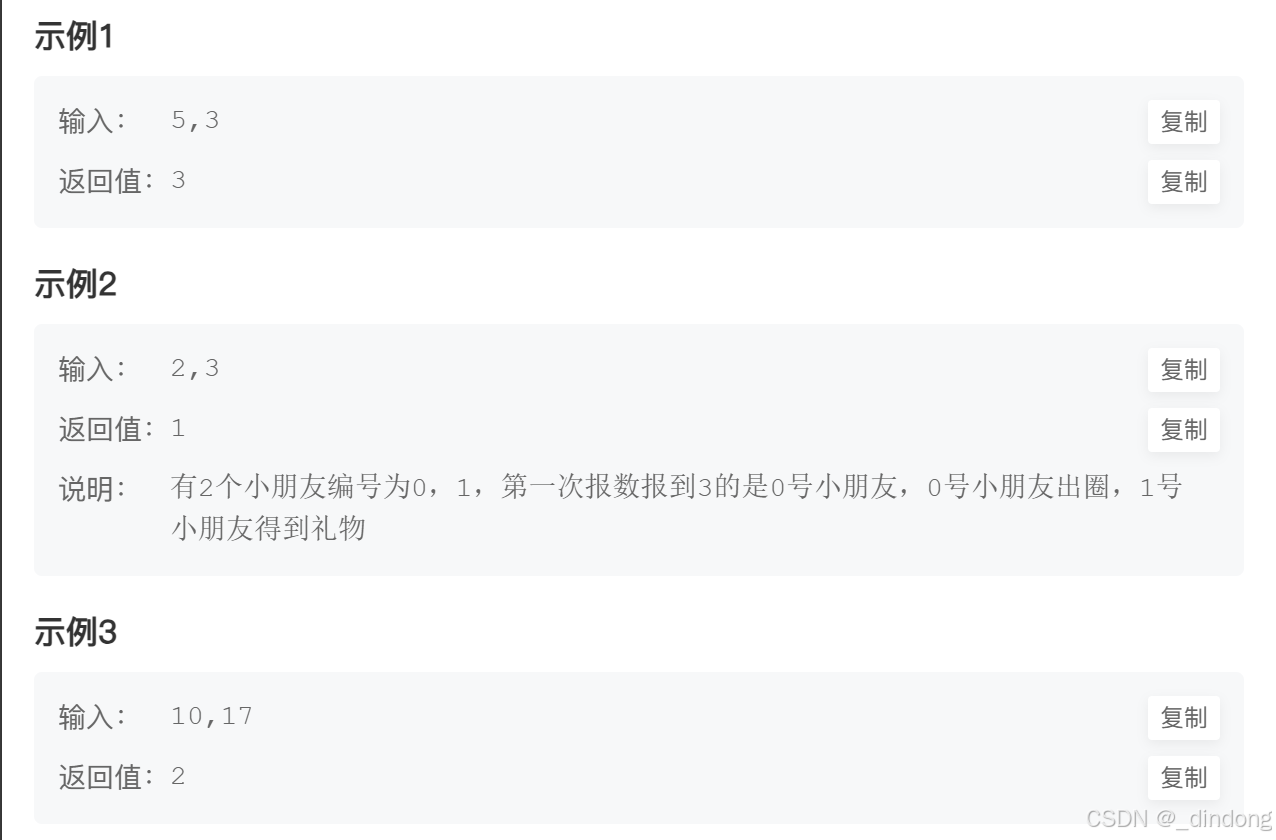
思路一：循环链表做

class Solution {
public:
    int LastRemaining_Solution(int n, int m) {
        if(n<1||m<1) return -1;
        //环形链表模拟
        list<int> nums;
        for(int i=0;i<n;++i) 
          nums.emplace_back(i);
        //开始进行模拟
        auto it=nums.begin();
        while(nums.size()>1){
          //开始数m
          for(int i=1;i<m;++i)
            if(++it==nums.end()) it=nums.begin();//越界了就要恢复
          it=nums.erase(it);//迭代器删除后返回的是被删除元素的下一个位置
          if(it==nums.end()) it=nums.begin();//可能恰好删除的是最后一个
        }
        return *it;
    }
};

思路二：dp[i]表示i个孩子时，获胜的孩子的下标，dp[1]=0，从2开始填，返回dp[n]。

dp[n]从0开始数，数到m-1，删掉这个位置，原本下标为m的位置从0开始，映射到n-1里面就是n里边的下标全部减去m，那么n-1映射到n就是下标加上m然后取模于n

class Solution {
public:
    int LastRemaining_Solution(int n, int m) {
        int f=0;
        for(int i=2;i<=n;++i) f=(f+m)%i;
        return f;
    }
};

16*.字符串中找到连续最长的数字串（模拟+双指针）

字符串中找出连续最长的数字串_牛客题霸_牛客网

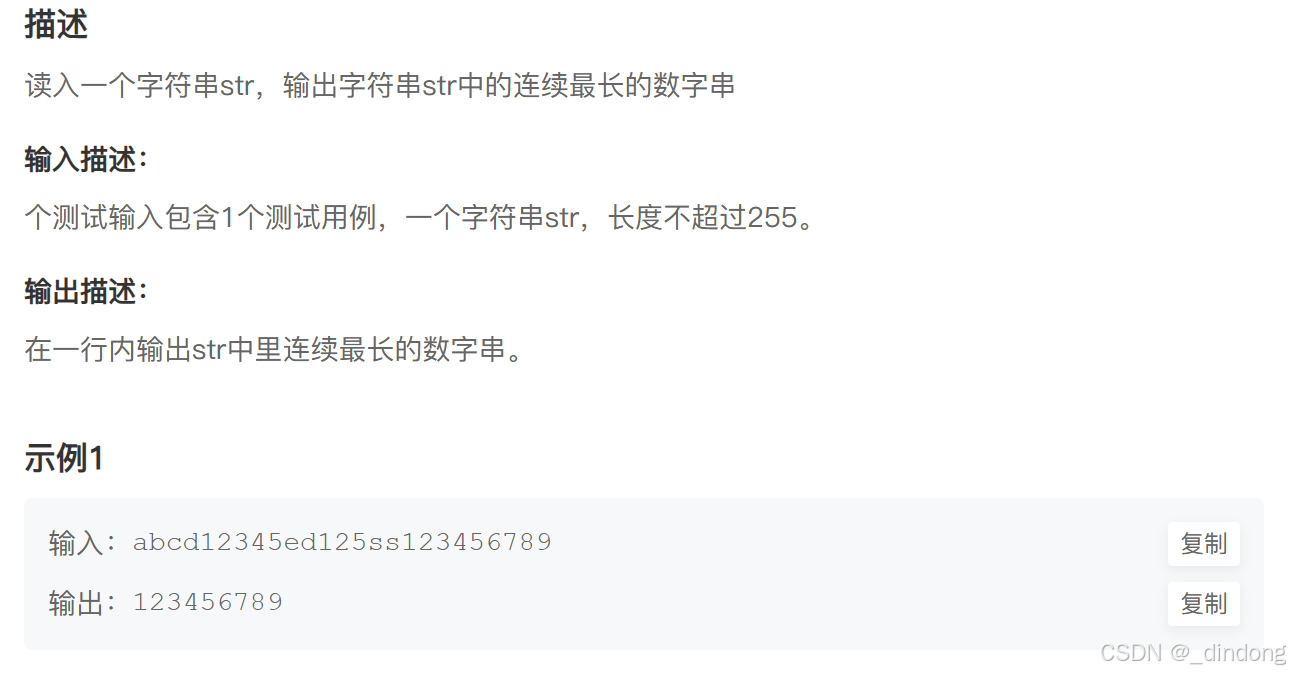
s.substr(pos,len)

#include<cctype> isdigit判断数字

#include <iostream>
#include <string>
#include <cctype>
using namespace std;
 
int main() {
    //双指针
    string str;
    cin>>str;
    int n=str.size();
    int begin=-1,len=0;
    for(int left=0;left<n;++left)
        if(isdigit(str[left])){//如果left是数字的话
           int right=left;
           while(right<n&&isdigit(str[right])) ++right;
           //走到这说明right在结尾的下一个位置
           if(right-left>len){
            begin=left;
            len=right-left;
           }
           left=right;//再++left 没事 因为该位置一定不是数字 可以跳过
        }
    if(begin==-1) cout<<""<<endl;
    else cout<<str.substr(begin,len)<<endl;
    return 0;
}
// 64 位输出请用 printf("%lld")

17*.岛屿数量（dfs)

岛屿数量_牛客题霸_牛客网

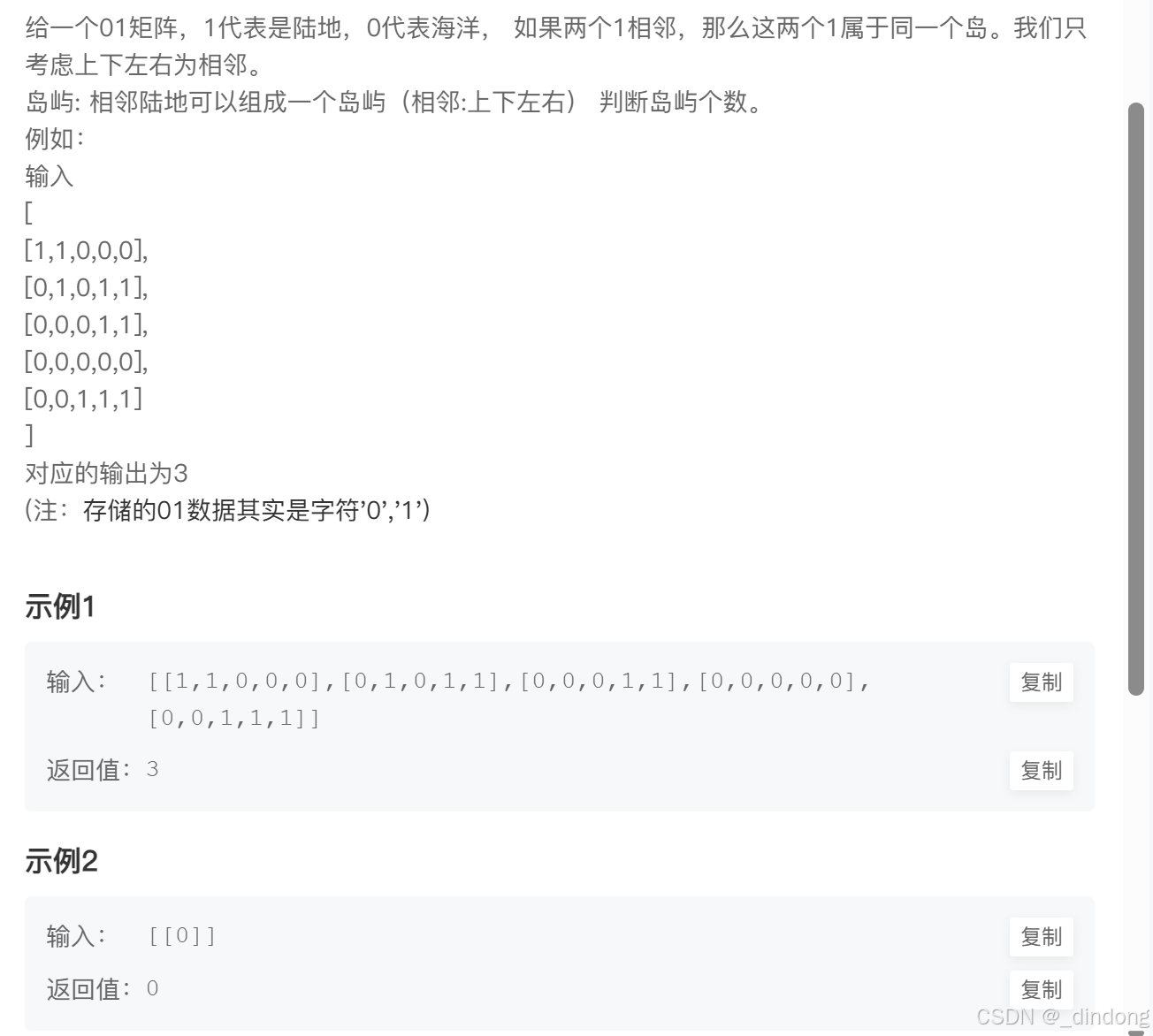
可以用check数组标记，本来以为这个备注的意思是边界最大为200x200的意思，开了201*201过不了，后来想想这可能仅仅代表面积，check数组开成301就能过。或者直接修改原数组也行

class Solution {
    int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1},m,n;
    bool check[301][301];
public:
    int solve(vector<vector<char>>& grid) {
        m=grid.size(),n=grid[0].size();
        int ret=0;
        for(int i=0;i<m;++i)
        {
            for(int j=0;j<n;++j)
            {
                if(grid[i][j]=='1'&&!check[i][j])
                {
                    ++ret;
                    //check!
                    dfs(grid,i,j);
                }
            }
        }
        return ret;
    }
    void dfs(vector<vector<char>>& grid,int i,int j)
    {
        check[i][j]=true;
        for(int k=0;k<4;++k)
        {
            int x=i+dx[k],y=j+dy[k];
            if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]=='1'&&!check[x][y])
            {
                dfs(grid,x,y);
            }
        }
    }
};

或者直接修改原数组

class Solution {
public:
    int m,n;
    int dx[4]={0,0,-1,1};
    int dy[4]={-1,1,0,0};
    int solve(vector<vector<char>>& grid) {
       m=grid.size(),n=grid[0].size();
       int ret=0;
       for(int i=0;i<m;++i)
         for(int j=0;j<n;++j)
           if(grid[i][j]=='1'){
              ++ret;//说明找到了一个岛屿
              dfs(grid,i,j);
           }
       return ret;
    }
    void dfs(vector<vector<char>>& grid,int i,int j){
        grid[i][j]='0';
        for(int k=0;k<4;++k){
            int x=dx[k]+i,y=dy[k]+j;
            if(x>=0&&x<m&&y>=0&&y<n&&grid[x][y]=='1') 
               dfs(grid,x,y);
        }
    }
};

18?.拼三角（枚举/dfs）

拼三角

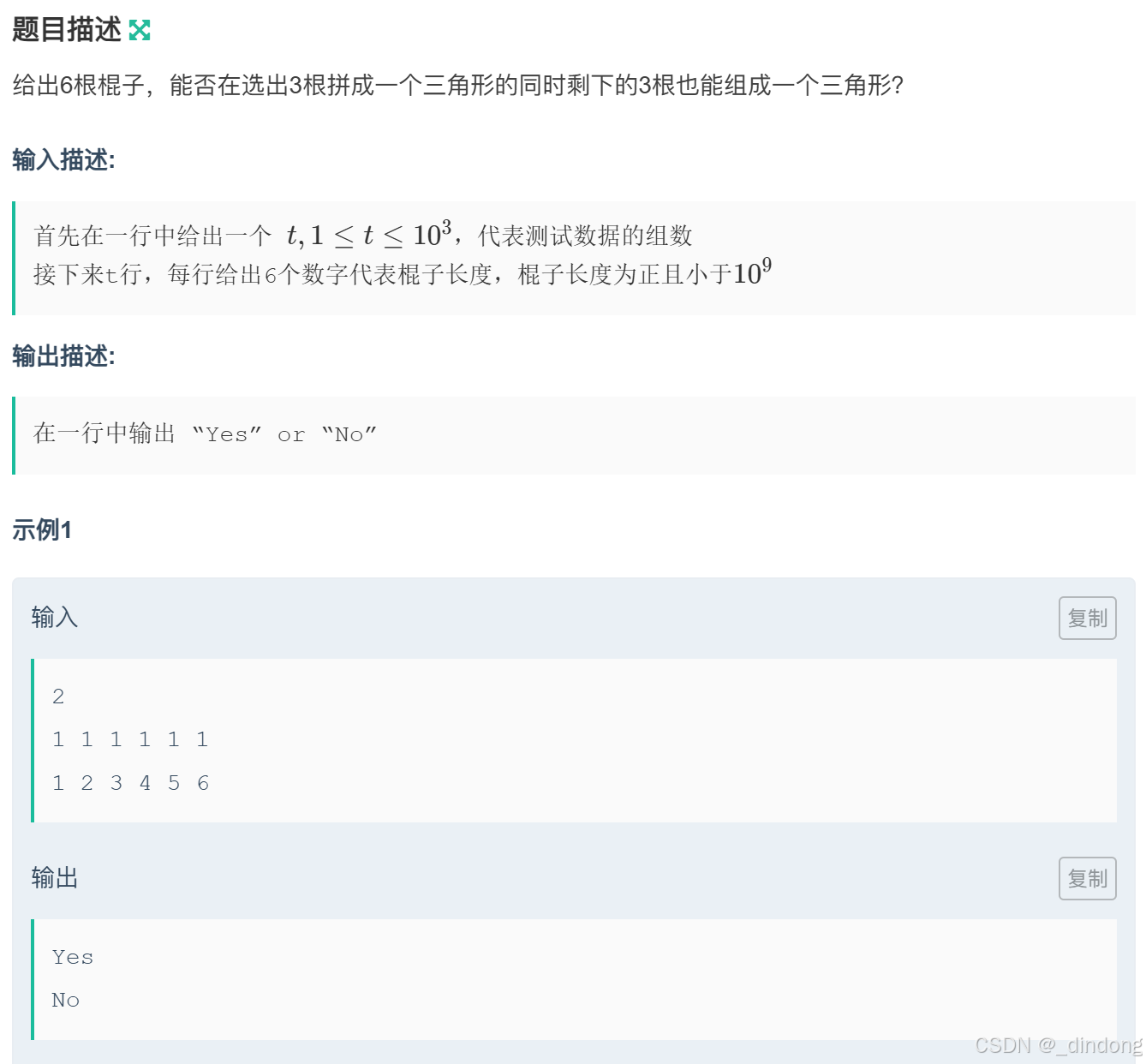
总共就10种情况，排序后优化枚举可以减少比对次数

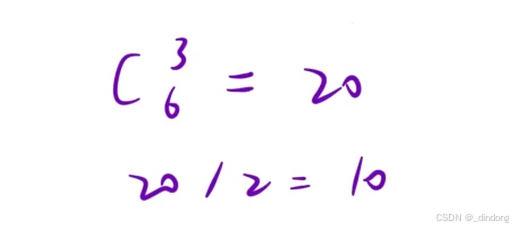
如此只需比对四次

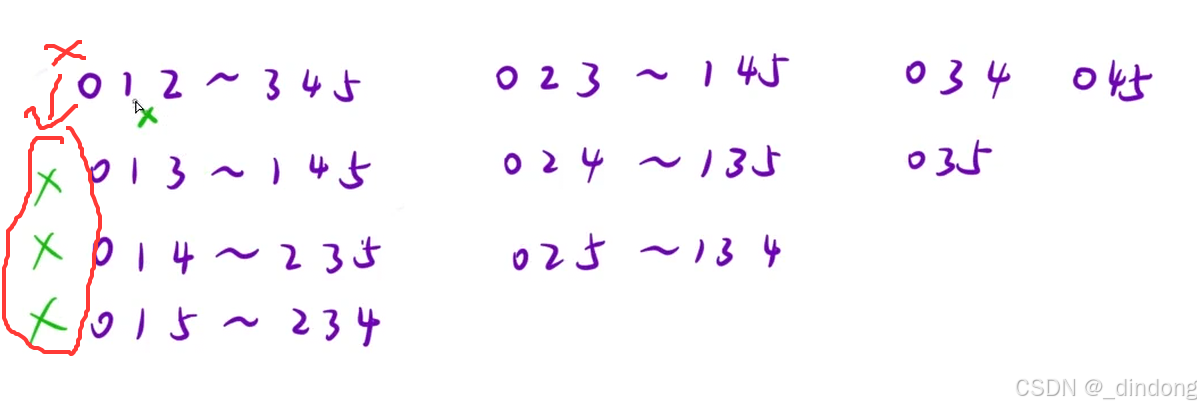
#include<iostream>
#include<algorithm>//算法头文件 记得会拼
//优化后的枚举 只需要考虑4种情况
//012-345 023-145 034-125 045-123
int a[6];
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        for(int i=0;i<6;++i) cin>>a[i];
        sort(a,a+6);//静态数组的用法
        if(a[0]+a[1]>a[2]&&a[3]+a[4]>a[5]||
           a[0]+a[2]>a[3]&&a[1]+a[4]>a[5]||
           a[0]+a[3]>a[4]&&a[1]+a[2]>a[5]||
           a[0]+a[4]>a[5]&&a[1]+a[2]>a[3])  cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

Week 1 ending.....