笔试强训：Week -5

原创 于 2025-11-21 21:43:17 发布 · 893 阅读 · 15 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#哈希算法 #散列表 #算法

目录

一*、笨小猴（哈希）

高效判断质数方法

二、主持人调度（排序）

三、分割等和子集（dfs子集问题 / 01背包）

四、小红的ABC（找规律）

五、不相邻取数（简单多状态dp）

六、空调遥控（排序+二分/滑动窗口）

七、kotori和气球（找规律）

八*、走迷宫（最短路bfs）

九**、主持人调度（贪心+优先级队列+排序）

十、游游的重组偶数（模拟）

十一**、体操队形（枚举+dfs）

十二**、二叉树中的最大路径和（dfs+树形dp）

十三**、排序子序列（模拟+贪心）

十四**、消减整数（贪心+数学）

十五**、最长上升系序列（贪心+二分）

十六、爱吃素（质数判断）

十七、相差不超过k的最多数（排序+滑动窗口）

十八**、最长公共子序列（LCS dp）

一*、笨小猴（哈希）

笨小猴_牛客题霸_牛客网

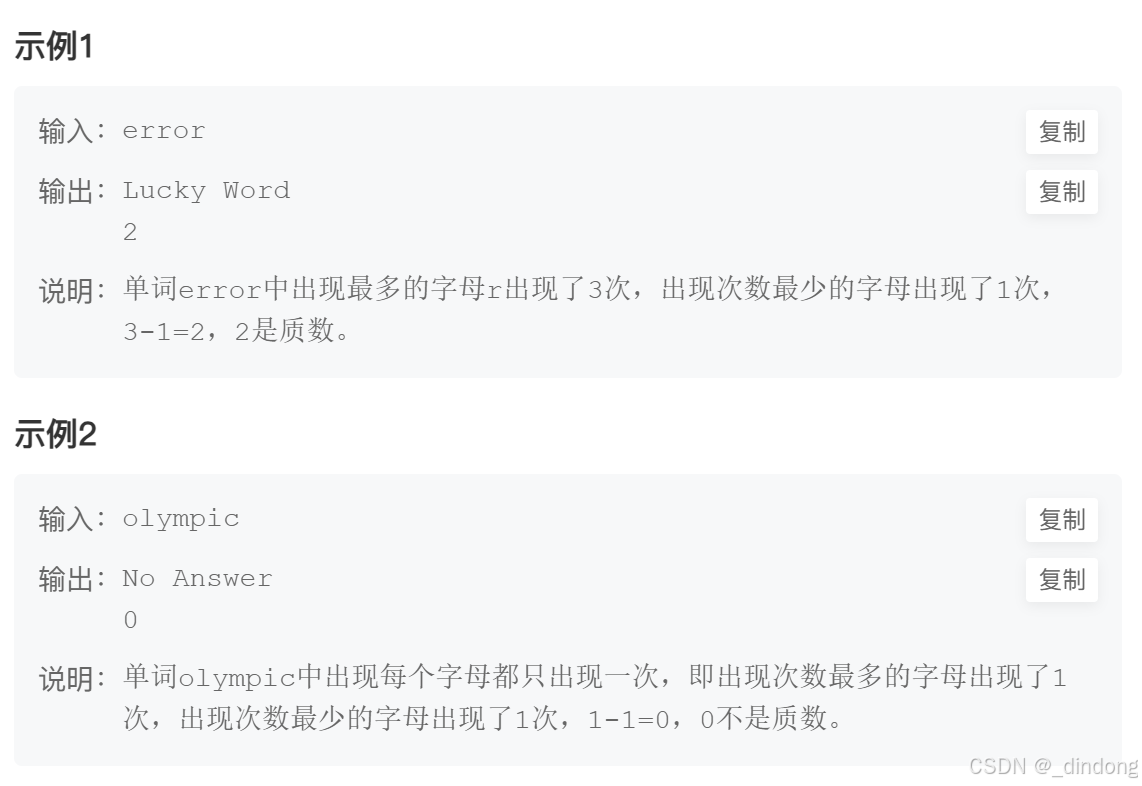
高效判断质数方法

bool isprime(int x){
    //试除法
    if(x==2) return true;
    if(x<2||x%2==0) return false;
    int n=sqrt(x);
    for(int i=3;i<=n;i+=2)
      if(x%i==0) return false;
    return true;
}

一直过百分之60，结果看错题，No Answer的时候直接输出0，而不是num

#include <algorithm>
#include <climits>
#include <cmath>
#include <iostream>
#include <ostream>
using namespace std;

bool isprime(int x){
    //试除法
    if(x==2) return true;
    if(x<2||x%2==0) return false;
    int n=sqrt(x);
    for(int i=3;i<=n;i+=2)
      if(x%i==0) return false;
    return true;
}
int main() {
    string s;
    cin>>s;
    // if(s=="")
    // {
    //     cout<<"No Answer"<<endl;
    //     cout<<"0";
    //     return 0;
    // }
    int hash[26]={0};
    int maxn=INT_MIN,minn=INT_MAX,cur=0;
    //遍历第一遍，统计所有字母出现次数
    while(cur<s.size())
    {
        ++hash[s[cur]-'a'];
        ++cur;
    }
    //再找出除0之外的，最大值最小值
    cur=0;
    for(;cur<26;++cur)
    {
        if(hash[cur]==0)continue;
        if(hash[cur]<minn)minn=hash[cur];
        if(hash[cur]>maxn)maxn=hash[cur];
    }
    int num=maxn-minn;
    if(isPrime(num)){
        cout<<"Lucky Word"<<endl;
        cout<<num;
    }
    else {
        cout<<"No Answer"<<endl;
        cout<<0;
    }
    return 0;
}

二、主持人调度（排序）

主持人调度（一）_牛客题霸_牛客网

人机题

class Solution {
public:
    bool hostschedule(vector<vector<int> >& schedule) {
        sort(schedule.begin(),schedule.end());
        for(int i=0;i<schedule.size()-1;++i)
        {
            if(schedule[i][1]>schedule[i+1][0])return false;
        }
        return true;
    }
};

三、分割等和子集（dfs子集问题 / 01背包）

分割等和子集_牛客题霸_牛客网

dfs解决子集问题

#include <iostream>
#include <vector>
using namespace std;
int arr[501];
int sum,n;
bool dfs(int arr[],int pos,int count)
{
    if(count==sum/2)return true;
    
    //选
    if(dfs(arr,pos+1,count+arr[pos]))return true;
    //不选
    if(dfs(arr,pos+1,count))return true;

    return false;
}
int main() {
    cin>>n;
    for(int i=0;i<n;++i){
        cin>>arr[i];
        sum+=arr[i];
    }
    if(sum%2)
    {
        cout<<"false";
        return 0;
    }
    if(dfs(arr,0,0))cout<<"true";
    else cout<<"false";

    return 0;
}

01背包

#include <iostream>
using namespace std;
//从数组中挑选一些数字 是否可以恰好等于sum/2  01背包问题
int n;
const int N=505,M=505*105/2;
int arr[N];
bool dp[M];
int main(){
  cin>>n;
  int sum=0;//记录总和
  for(int i=1;i<=n;++i){
    cin>>arr[i];
    sum+=arr[i];
  }
  if(sum%2) cout<<"false"<<endl;//不能整除
  else{
    sum/=2;
    dp[0]=true;
    for(int i=1;i<=n;++i)
      for(int j=sum;j>=arr[i];--j)
         dp[j]=dp[j]||dp[j-arr[i]];
    if(dp[sum]) cout<<"true"<<endl;
    else cout<<"false"<<endl;
  }

  return 0;
}

四、小红的ABC（找规律）

小红的ABC

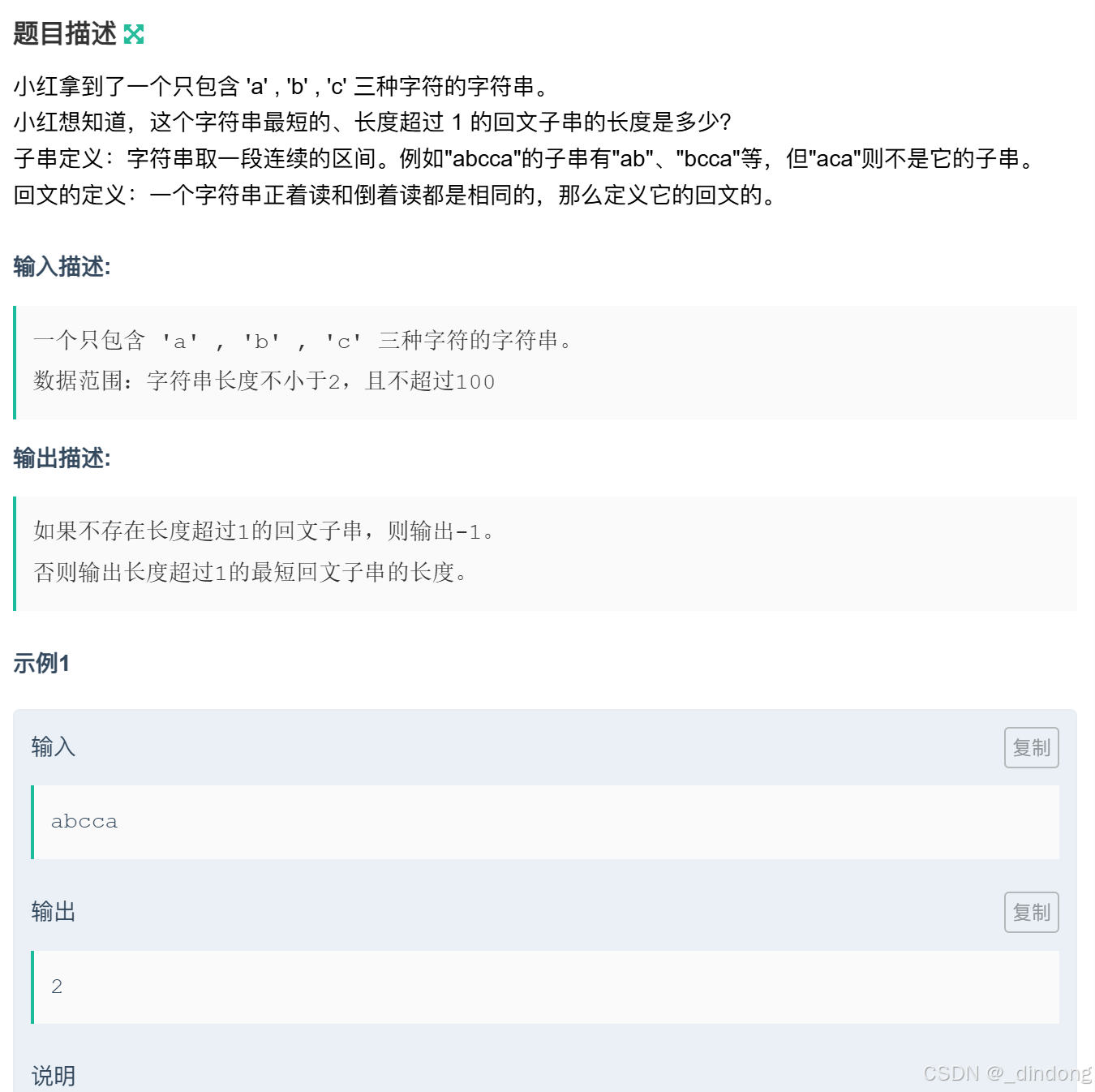
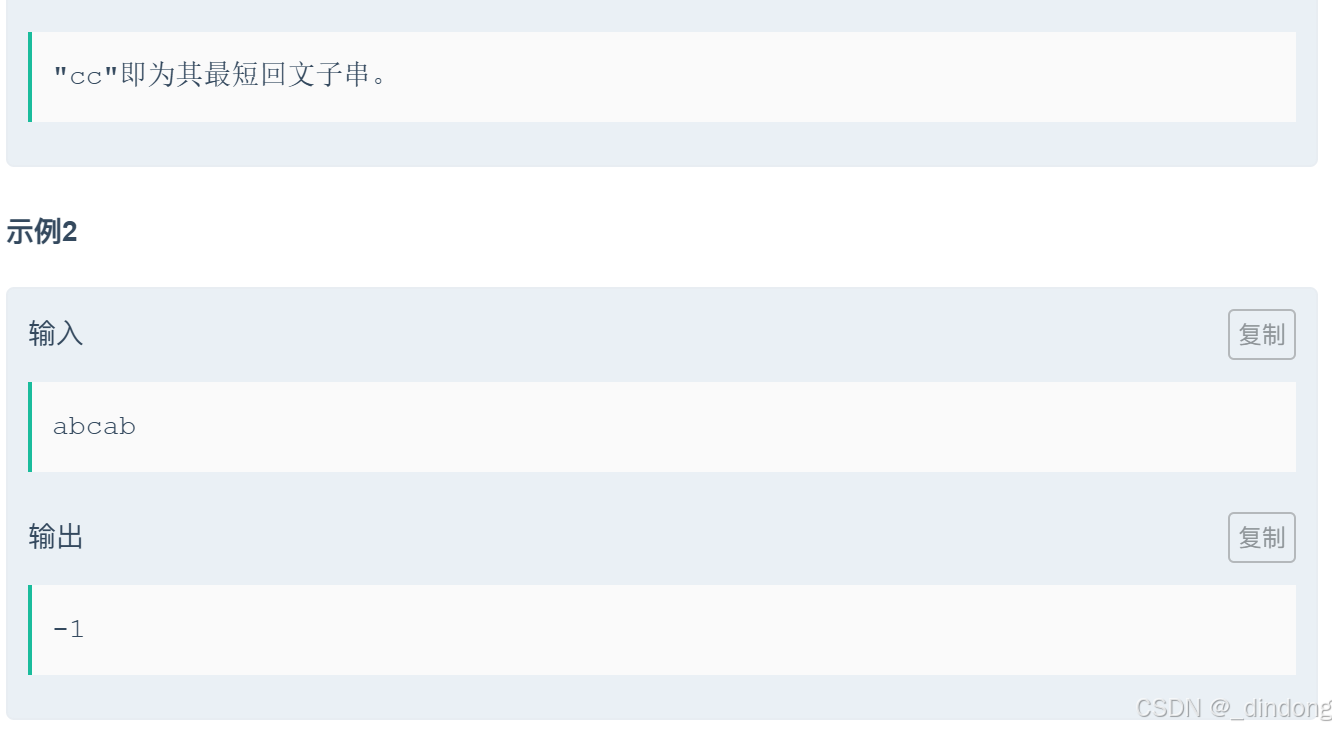
以为是求最长回文子串长度，结果是找最短的回文子串（长度不为1）长度。那么仅需判断长度为2或者长度为3的子串即可

//a b c三个字母 最短的 那么只有可能是2和3
#include<iostream>
#include<string>
using namespace std;
string s;
int main(){
    cin>>s;
    int n=s.size();
    int ret=-1;//没有回文串的情况
    for(int i=0;i<n-1;++i){
        if(s[i]==s[i+1]){
            ret=2;
            break;
        }
        if(i+2<n&&s[i]==s[i+2]) ret=3;
    }
    cout<<ret<<endl;
    return 0;
}

五、不相邻取数（简单多状态dp）

不相邻取数_牛客题霸_牛客网

题目给的n范围有问题啊，开大点能过

#include <iostream>
#include <vector>
using namespace std;
int n;
long long arr[200001];
int main() {
    cin>>n;
    for(int i=0;i<n;++i)cin>>arr[i];
    vector<long long> f(n+1);
    auto g=f;
    for(int i=1;i<=n;++i)
    {
        f[i]=g[i-1]+arr[i-1];
        g[i]=max(g[i-1],f[i-1]);
    }
    cout<< max(f[n],g[n]);
    return 0;
}

六、空调遥控（排序+二分/滑动窗口）

空调遥控

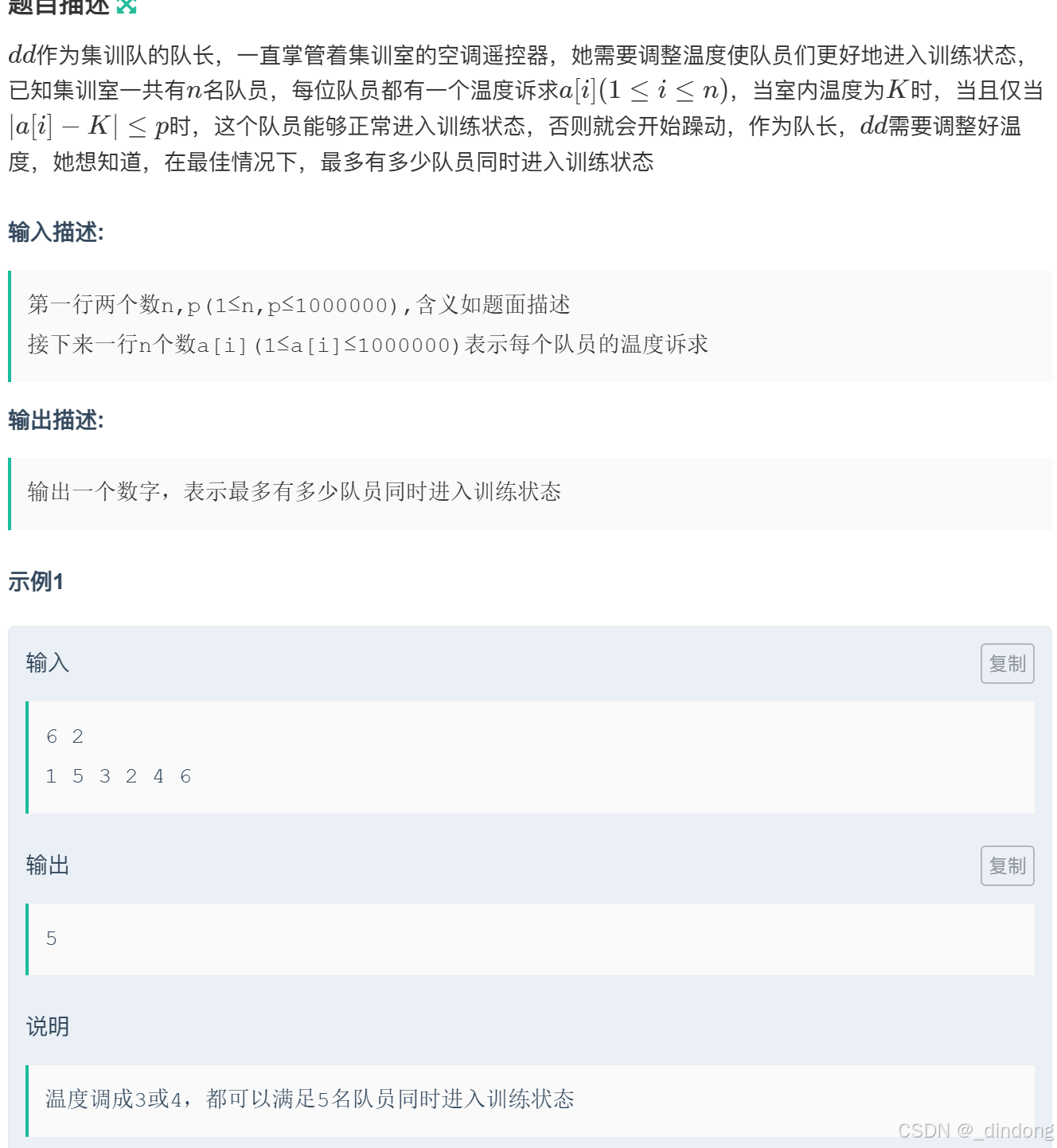
排序后暴力做的，超时了，通过率百分之0

解法1：排序+二分找区间（左端点+右端点组合）

范围题要优化的话就是二分！！！！

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e6+10;
int arr[N];
int n,p;
int main(){
    cin>>n>>p;
    for(int i=0;i<n;++i) cin>>arr[i];
    sort(arr,arr+n);
    int ret=1;
    //开始枚举
    for(int i=arr[0];i<=arr[n-1];++i){//枚举温度
        int left=0,right=n-1;
        while(left<right){//begin：左端点
            int mid=left+(right-left)/2;
            if(arr[mid]<i-p) left=mid+1;
            else right=mid;
        }
       int begin=left;
       right=n-1;//left可以继续从原来的位置找 重置right就行了
       while(left<right){//right：右端点
            int mid=left+(right-left+1)/2;
            if(arr[mid]<=i+p) left=mid;
            else right=mid-1;
        }
       ret=max(ret,right-begin+1);
    }
    cout<<ret<<endl;
    return 0;
}

解法二：滑动窗口

竟然没想到，脑子被课设干扰了fa ke

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e6+10;
int arr[N];
int n,p;
int main(){
    cin>>n>>p;
    p*=2;//差值
    for(int i=0;i<n;++i) cin>>arr[i];
    sort(arr,arr+n);
    //滑动窗口 差值在2*p的最大区间
    int ret=1;
    for(int left=0,right=0;right<n;++right){
        while(arr[right]-arr[left]>p)++left;
        ret=max(ret,right-left+1);
    }
    cout<<ret<<endl;
}

七、kotori和气球（找规律）

kotori和气球

乍一眼我还以为第一题就上动规呢，看懂后很简单

#include <iostream>
using namespace std;
const int MOD=109;
int main() {
    int n,m;
    cin>>n>>m;
    long long ans=n;
    for(int i=1;i<m;++i)ans=(ans*(n-1))%MOD;
    cout<<ans;
    return 0;
}

八*、走迷宫（最短路bfs）

走迷宫_牛客题霸_牛客网

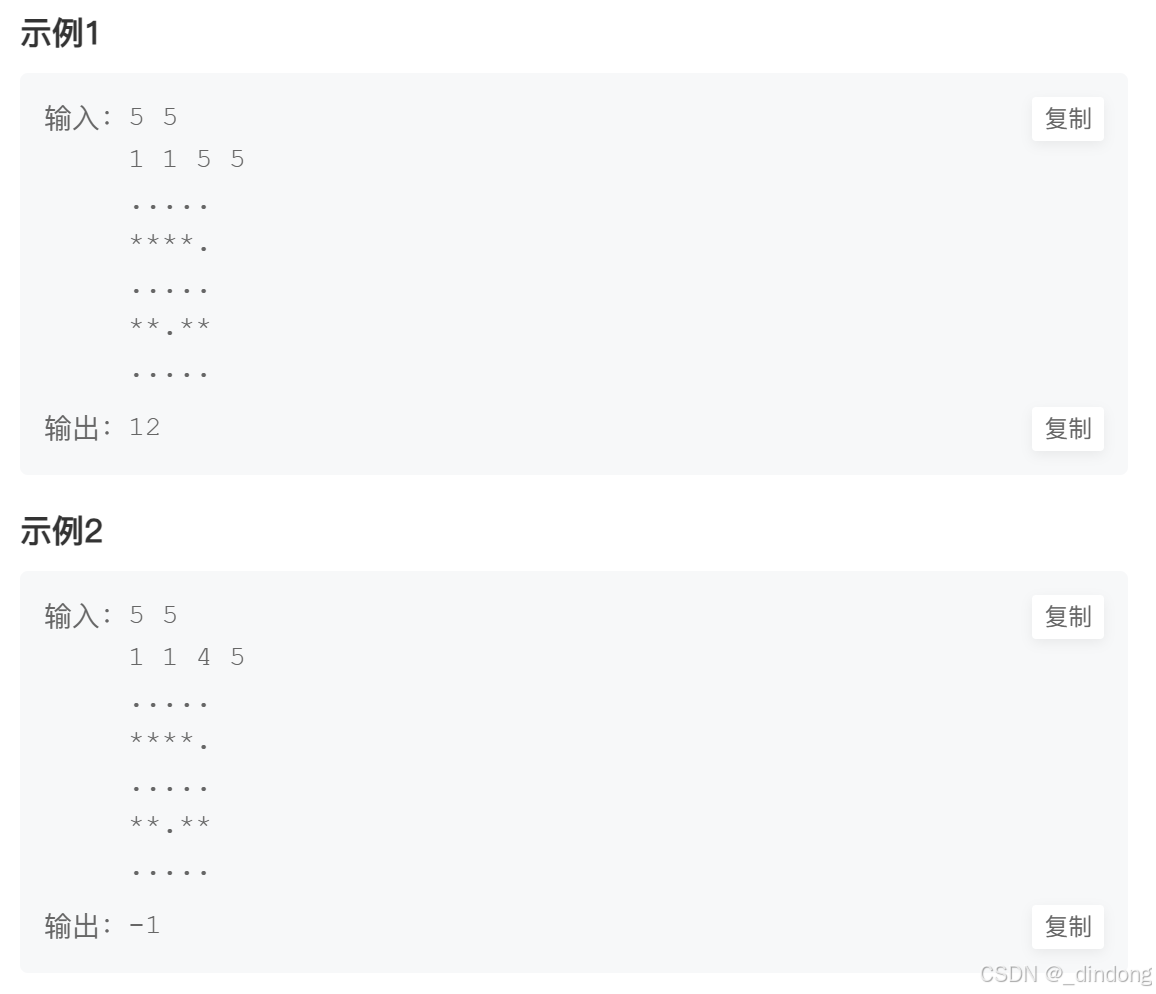
第一遍写了错误代码，体现了dfs，但没有体现最短路，代码会按照一条路先走到黑，如果到达了，则输出结果，但并不是最短路。正确是bfs层序遍历才能最短路。。。

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N=1010;
int dx[4]={0,0,-1,1};
int dy[4]={-1,1,0,0};
int n,m,x1,x2,y1,y2;
char arr[N][N];
int dis[N][N];//不仅用来看看搜索过了没 
//单源最短路问题 用bfs扩展
int bfs(){//-1表示走不到
   if(arr[x2][y2]=='*') return -1;
   memset(dis, -1, sizeof dis); // 表⽰还没开始搜索
   queue<pair<int,int>> q;
   q.emplace(x1,y1);
   dis[x1][y1]=0;
   while(!q.empty()){
       auto[a,b]=q.front();
       q.pop();
       for(int k=0;k<4;++k){
        int x=dx[k]+a,y=dy[k]+b;
        if(x>=1&&x<=n&&y>=1&&y<=m&&arr[x][y]=='.'&&dis[x][y]==-1){
            q.emplace(x,y);
            dis[x][y]=dis[a][b]+1;
            if(x==x2&&y==y2) return dis[x][y];
        }
       }
   }
   return -1;
}
int main() {
   cin>>n>>m>>x1>>y1>>x2>>y2;
   for(int i=1;i<=n;++i)
       for(int j=1;j<=m;++j) cin>>arr[i][j];
   cout<<bfs()<<endl;
   return 0;
}

九**、主持人调度（贪心+优先级队列+排序）

主持人调度（二）_牛客题霸_牛客网

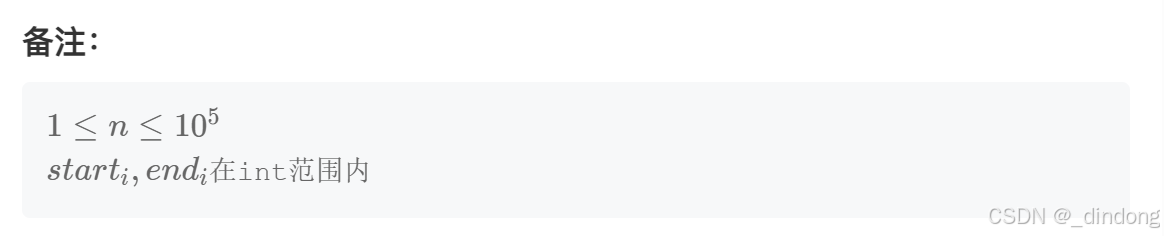
做题时还有些许印象，能感觉到这是一道贪心题，但思路已经忘光了。想的时候也往下面思路想了，但是没想到用小根堆。

class Solution {
public:
    int minmumNumberOfHost(int n, vector<vector<int>>& startEnd) {
       sort(startEnd.begin(),startEnd.end());
       priority_queue<int,vector<int>,greater<int>> heap;//创建一个小根堆
       heap.push(startEnd[0][1]);
       for(int i=1;i<n;++i){
        int a=startEnd[i][0],b=startEnd[i][1];
        if(a>=heap.top()) heap.pop(); //说明没有重叠
        heap.push(b);
       }
       return heap.size();
    }
};

或者分别排序+遍历比较

class Solution {
public:
    int minmumNumberOfHost(int n, vector<vector<int> >& startEnd) {
        vector<int> start;
        vector<int> end;
        //分别得到活动起始时间
        for(int i = 0; i < n; i++){
            start.push_back(startEnd[i][0]);
            end.push_back(startEnd[i][1]);
        }
        //分别对开始和结束时间排序
        sort(start.begin(), start.end());
        sort(end.begin(), end.end());
        int res = 0;
        int j = 0;//遍历结束时间
        for(int i = 0; i < n; i++)
            //新开始的节目大于上一轮结束的时间，主持人不变
            if(start[i] >= end[j])  j++;  
            else res++;  //主持人增加
        return res;
    }
};

十、游游的重组偶数（模拟）

游游的重组偶数__牛客网

必须得是从右往左第一个偶数放到最后才通过，正着来不给通过

#include <iostream>
#include <string>
using namespace std;
//把每个数字中为偶数的部分放到最后就可以了
int q;
string s;
int main() {
    cin>>q;
    while(q--){
        cin>>s;
        int n=s.size();
        int i=n-1;
        for(;i>=0;--i)
           if(s[i]%2==0){
            swap(s[i],s[n-1]);
            break;
           }
        if(i!=-1) cout<<s<<endl;
        else cout<<-1<<endl;
    }
}

十一**、体操队形（枚举+dfs）

体操队形

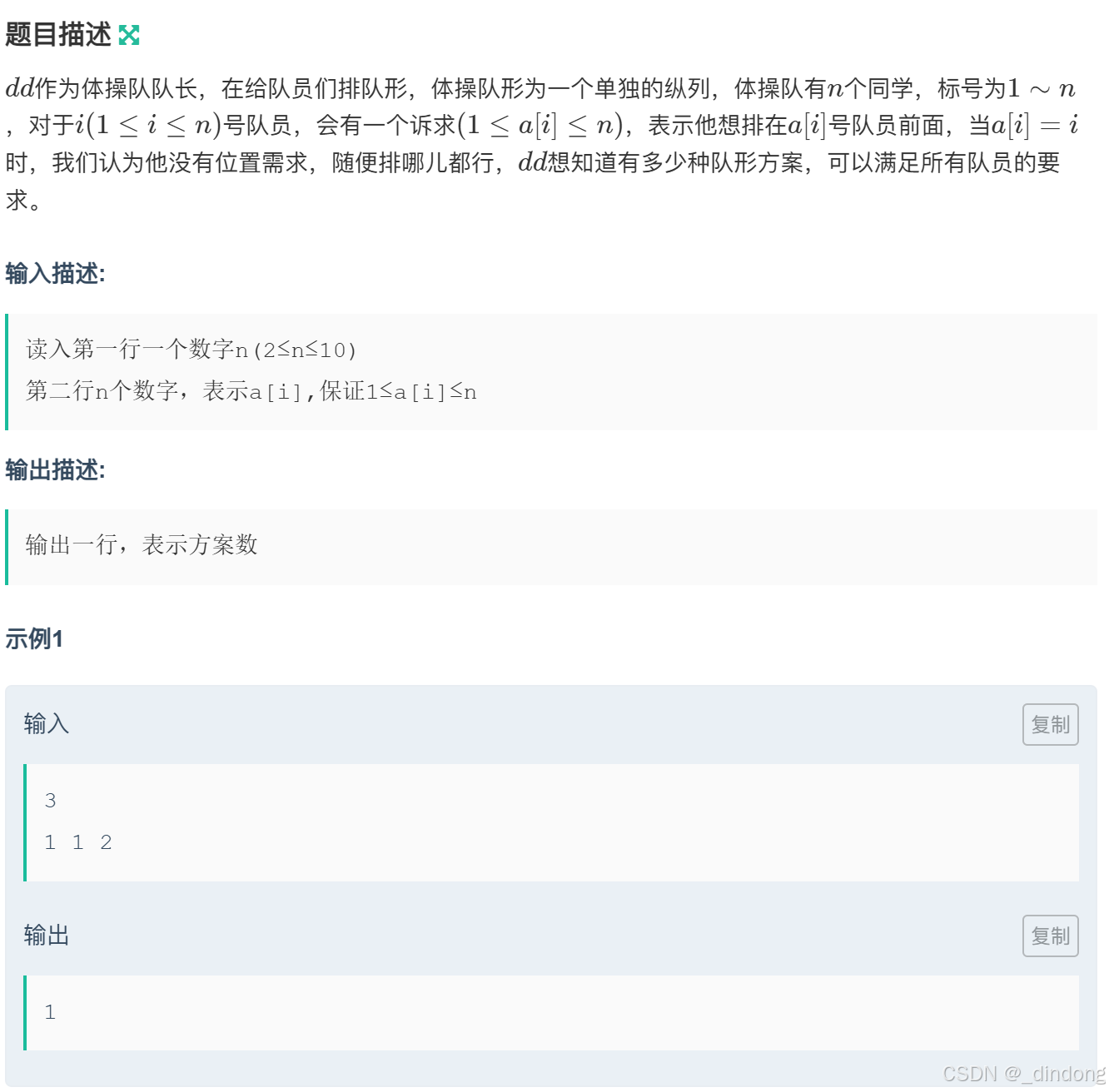
没思路，数据量比较少的时候可能就要用递归了（huaji）

#include<iostream>
using namespace std;
int n;
int ret=0;//统计最终结果
const int N=11;
int arr[N];
bool vis[N];//队员
void dfs(int pos){
    if(pos==n+1){
        ++ret;
        return;
    }//说明找到了一种合法方案
    //开始一个个位置去选择
    for(int i=1;i<=n;++i){
        if(vis[i]) continue;//如果该位置的人选过了 就跳过
        //我不可能排在我想排的人前面 那后面再怎么选都是错的
        if(vis[arr[i]]) return;
        vis[i]=true;
        dfs(pos+1);
        vis[i]=false;
    }
}
int main(){
    cin>>n;
    for(int i=1;i<=n;++i) cin>>arr[i];
    dfs(1);//从第一个位置开始选
    cout<<ret<<endl;
    return 0;
}

十二**、二叉树中的最大路径和（dfs+树形dp）

二叉树中的最大路径和_牛客题霸_牛客网

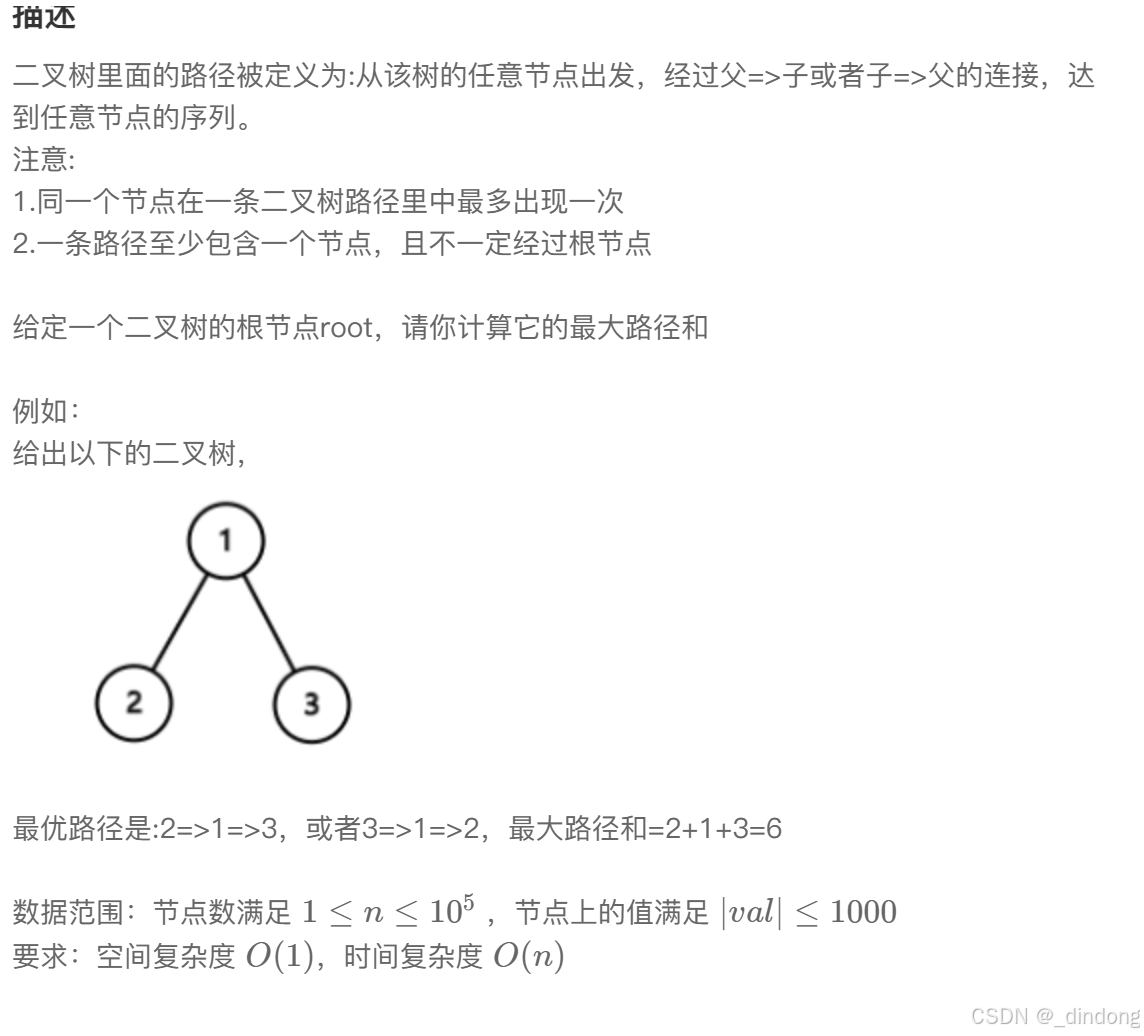
服了，为什么笔试题示例不给全啊

class Solution {
public:
    int ret=-1010;//统计最大值
    int maxPathSum(TreeNode* root) {
        dfs(root);
        return ret;
    }
    int dfs(TreeNode* root){
        if(root==nullptr) return 0;
        int left=max(dfs(root->left),0);//最大左子链
        int right=max(dfs(root->right),0);//最大右子链
        ret=max(ret,left+right+root->val);//经过root的最大路径
        return root->val+max(left,right);//给上层返回单链的信息
    }
};

难死了啊，今天三题就写出来半道，道心破碎一秒钟。

十三**、排序子序列（模拟+贪心）

排序子序列_牛客笔试题_牛客网

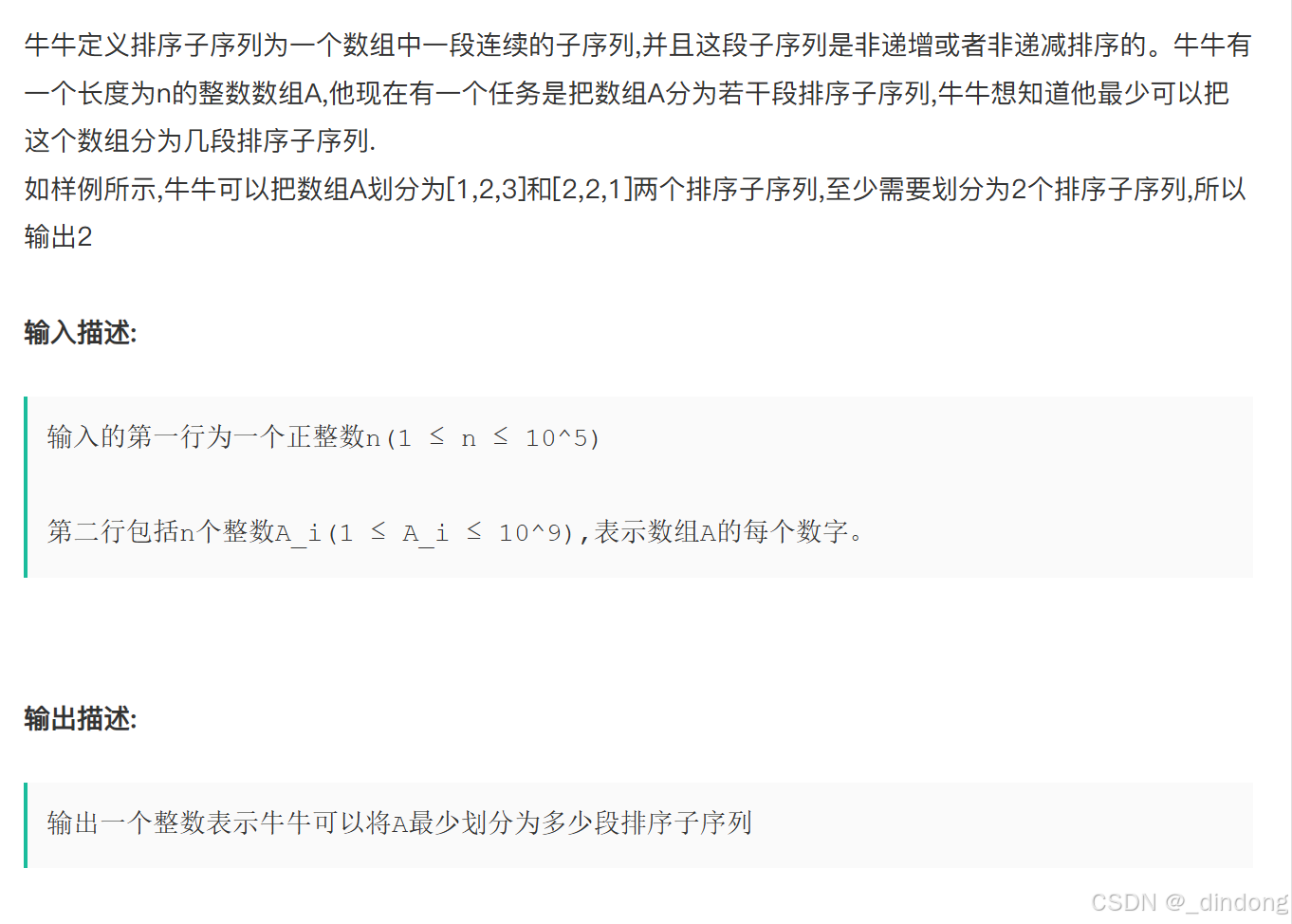
这里非递增和非递减都是非严格递增，非严格递减的意思。

#include <iostream>
using namespace std;
int n;
const int N=1e5+10;
int arr[N];
int main() {
  cin>>n;
  for(int i=0;i<n;++i) cin>>arr[i];
  int ret=0,i=0;
  while(i<n){
    if(i==n-1){//这个时候不存在后面的数比了 所以自己就是一个子序列
        ++ret;
        break;
    }
    if(arr[i+1]>arr[i]){//搞一个上升的子序列
       while(i+1<n&&arr[i+1]>=arr[i]) ++i;
       ++ret;
    }
    else if(arr[i+1]<arr[i]){//说明搞一个下降的子序列
       while(i+1<n&&arr[i+1]<=arr[i]) ++i;
       ++ret;
    }
    else  while(i+1<n&&arr[i+1]==arr[i]) ++i;
    ++i;
  }
  cout<<ret<<endl;
  return 0;
}

十四**、消减整数（贪心+数学）

消减整数

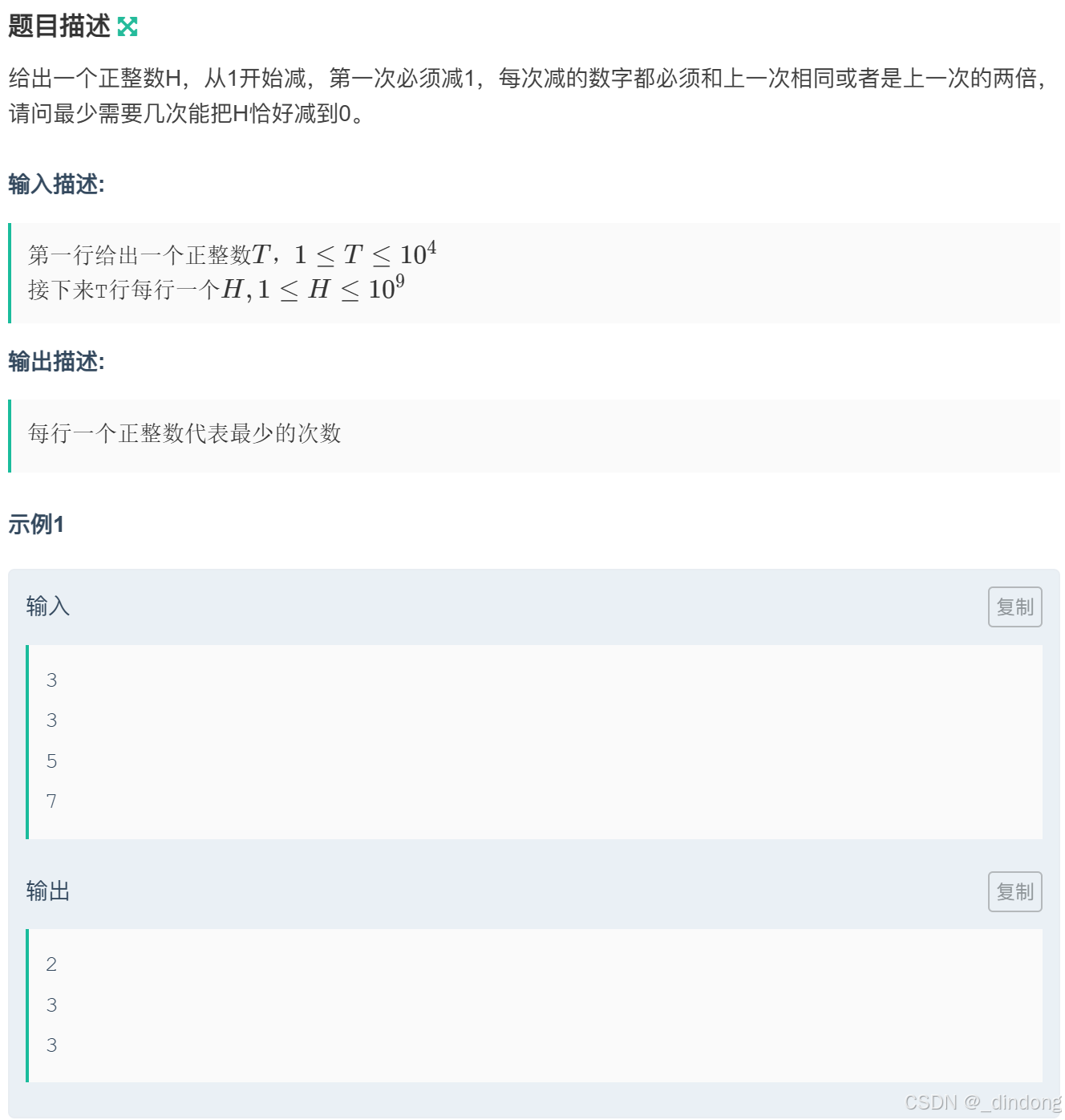
#include<iostream>
using namespace std;
int t,h;
int main(){
    cin>>t;
    while(t--){
        cin>>h;
        int a=1,ret=0;
        while(h){
            h-=a;
            ++ret;
            //因为得确保减到0，如果取模a*2没有余数，那么后续h减去a*2
            //就一定可以减到0，同时我们需要减到0最小次数，所以a*=2
            if(h%(a*2)==0) a*=2;
        }
        cout<<ret<<endl;
    }
    return 0;
}

十五**、最长上升系序列（贪心+二分）

最长上升子序列(二)_牛客题霸_牛客网

写动规干超时了，题目要求时间复杂度nlogn，都logn了肯定得考虑二分，这里求子序列的问题用动规解法就不提及了，直接提供更优的解法：贪心+二分

eg：

如此，保证递增性的同时，还能维护最小末尾（保证后边能插入更多数）同时还因为递增性利用二分，最优化算法。

以下是我个人总结，看不懂的可以直接看ai生成的解释：

我们不关心前面的序列长啥样，只关心长度为x的最小末尾是多少，后续是否会更新长度为x的最小末尾的元素不会和我们求最长递增子序列违背，因为填表的顺序是从前往后的，如果长度能有x，遍历到第i个数，如果大于当前最大长度也就是x末尾元素，就push_back，子序列最长长度肯定可以加一，如果是等于跳过，如果小于，就在当前数组二分查找可以更新哪个长度的最小末尾元素，因为更新的位置是恰好结果为小于的第一个位置，这样因为更新的元素更小，这不影响递增性，同时如果更新的元素是在最长长度的那个位置，后续遍历的时候就有可能插入更多的数，贪心算法就此体现。

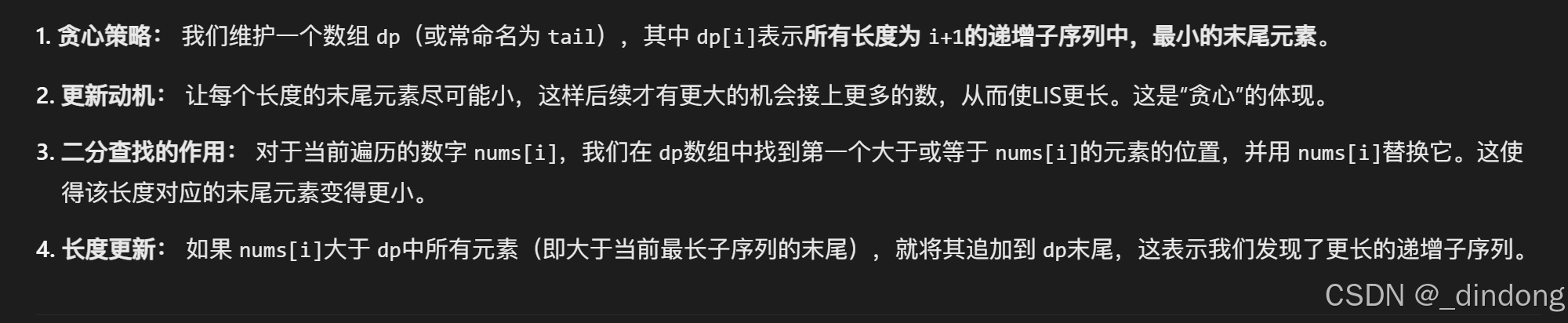
难啊/(ㄒoㄒ)/~~

十六、爱吃素（质数判断）

爱吃素

#include <cmath>
#include <iostream>
#include <ostream>
using namespace std;
bool IsPrime(long long x)
{
    if(x<=1)return false;
    if(x%2==0)return false;

    for(int i=3;i<=sqrt(x);i+=2)
    {
        if(x%i==0)return false;
    }
    return true;
}
int main() {
    int T;
    cin>>T;
    while(T--)
    {
        long long a,b;
        cin>>a>>b;
        if(IsPrime(a*b))cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    return 0;
}

十七、相差不超过k的最多数（排序+滑动窗口）

相差不超过k的最多数_牛客题霸_牛客网

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int n,k;
    cin>>n>>k;
    vector<int> arr(n);
    for(int i=0;i<n;++i)cin>>arr[i];
    sort(arr.begin(),arr.end());
    //滑动窗口
    int left=0,right=0,len=1;
    while(right<n)
    {
        while(arr[right]-arr[left]>k)++left;
        len=max(len,right-left+1);
        ++right;
    }
    cout<<len;
    return 0;
}

十八**、最长公共子序列（LCS dp）

最长公共子序列(一)_牛客题霸_牛客网

#include <iostream>
using namespace std;
const int N=1010;
char s1[N],s2[N];
int dp[N][N];
int n,m;
int main() {

   //dp[i][j]表示以0-i的字符串1中 与0-j字符串2中 的最长公共子序列长度
   cin>>n>>m;
   for(int i=1;i<=n;++i) cin>>s1[i];
   for(int i=1;i<=m;++i) cin>>s2[i];

   //开始进行dp
   for(int i=1;i<=n;++i)
     for(int j=1;j<=m;++j)
       if(s1[i]==s2[j]) dp[i][j]=dp[i-1][j-1]+1;
       else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
   cout<<dp[n][m]<<endl;

   return 0;
}

本周完结撒花*★,°*:.☆(￣▽￣)/$:*.°★* 。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

_dindong

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值