McCabe度量法

 计算有向图G的环路复杂性的公式为：V（G）= E-N+2 或 V（G）= 闭合区域+1

E=edge 边数 ，N=node 结点数

例题
一、McCabe度量法是通过定义环路复杂度，建立程序复杂性的度量，它基于一个程序模块的程序图中环路的个数。下图所示程序图的程序复杂度是（B）。

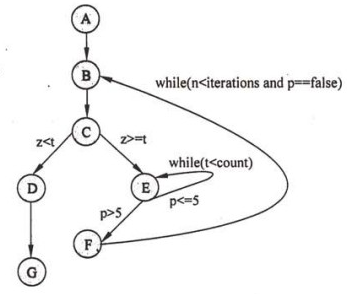
A.2   B.3   C.4   D.5

有向弧数：8
节点数：7
V（G）= 有向弧数-节点数+2 = 3
闭合区域：2
V（G）= 闭合区域+1 = 3

二、某程序的程序图如下所示，运用McCabe度量法对其进行度量，其环路复杂度是（D）。

A.2   B.3   C.4   D.5

有向弧数：10
节点数：7
V（G）= 有向弧数-节点数+2 = 5
闭合区域：4
V（G）= 闭合区域+1 = 5

三、某程序的程序图如下图所示，运用McCabe度量法对其进行度量，其环路复杂度是（C）。

A.4   B.5   C.6   D.8

有向弧数：11
节点数：7
V（G） = 有向弧数-节点数+2 = 6
封闭区域 = 5
V（G） = 闭合区域+1 = 6

四、McCabe度量法，以下程序图的复杂性度量值为（A）。

A.4   B.5   C.6   D.7

有向弧数：9
节点数：7
V（G） = 有向弧数-节点数+2 = 4
封闭区域：3
V（G）= 封闭区域+1 = 4

五、采用McCabe度量法计算下列程序图的环路复杂性为（）。

A.2   B.3   C.4   D.5

有向弧数：10
节点数：9
V（G） = 有向弧数-节点数+2 = 3
封闭区域：2
V（G） = 封闭区域+1 = 3

六、采用McCabe度量法计算下图的环路复杂件为（）。

A.2   B.3   C.4   D.5

 

解析：在一个强连通的有向图G中，环的个数为m-n+2p。其中m为图中弧的个数，n为图中的结点数，p是图中强连通分量的个数。题图为一强连通图，故p=1，而图中弧的个数为8，结点数为6，故环的个数为8-6+2=4。

七、若采用McCabe度量法计算环路复杂性，则对于下图所示的程序图，其环路复杂度为（）。

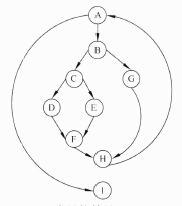
A.2   B.3   C.4   D.5

有向弧数：11
节点数：9
V（G） = 有向弧数-节点数+2 = 4
封闭区域：3
V（G） = 封闭区域+1 = 4

(2014年上半年软件设计师上午试卷32题) 采用McCabe度量法计算下列程序图的环路复杂性为（）。

 

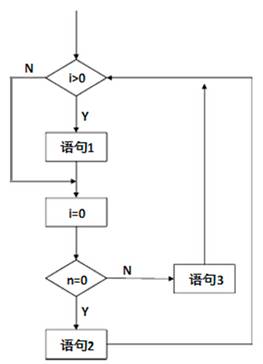
A.2   B.3   C.4   D.5

有向弧数：12
节点数：10
V（G） = 有向弧数-节点数+2 = 4
封闭区域：3
V（G） = 封闭区域+1 = 4

(2014年下半年软件设计师上午试卷35题) 采用McCabe度量法计算该程序图的环路复杂性为（）。

 

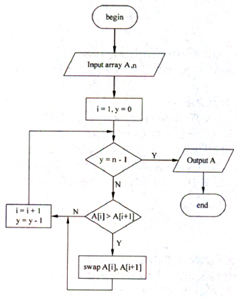
A.3   B.4   C.5   D.6

有向弧数：12
节点数：11
V（G） = 有向弧数-节点数+2 = 3
封闭区域：2
V（G） = 封闭区域+1 = 3

(2015年上半年软件设计师上午试卷35题) 采用McCabe度量法计算下列程序图的环路复杂性为（）。

 

A.2   B.3   C.4   D.5

有向弧数：10
节点数：8
V（G） = 有向弧数-节点数+2 = 4
封闭区域：3
V（G） = 封闭区域+1 = 4

(2016年上半年软件设计师上午试卷36题) 采用McCabe度量法计算下图所示程序的环路复杂性为（）。

 

A.1   B.2   C.3   D.4

有向弧数：11
节点数：10
V（G） = 有向弧数-节点数+2 = 3
封闭区域：2
V（G） = 封闭区域+1 = 3

(2016年下半年软件设计师上午试卷33题)对下图采用McCabe度量法计算该程序的环路复杂性为（）。

 

A.1   B.2   C.3   D.4

补充有向弧和节点

有向弧数：13
节点数：11
V（G） = 有向弧-节点数+2 = 4
封闭区域：3
V（G） = 封闭区域+1 = 4

(2017年上半年软件设计师上午试卷36题)对下图所示的程序流程图采用 McCabe 度量法计算其环路复杂度为（）。

 

A.1   B.2   C.3   D.4

补充有向弧和节点

有向弧数：16
节点数：14
V（G） = 有向弧数-节点数+2 = 4
封闭区域：3
V（G） = 封闭区域+1 = 4

(2018年上半年软件设计师上午试卷35题)对下图所示的程序流程图采用McCabe度量法计算器环路复杂度为（）。

 

A.2   B.3   C.4  D.5

补充有向弧和节点

有向弧数：13
节点数：12
V（G） = 有向弧数-节点数+2 = 3
封闭区域：2
V（G） = 封闭区域+1 = 3

(2018年下半年软件设计师上午试卷35题)对以下的程序伪代码(用缩进表示程序块)采用McCabe度量法计算其环路复杂度为（）。

A.2  B.3   C.4   D.5

 

补充有向弧和节点

 

有向弧数：20
节点数：18
V（G） = 有向弧数-节点数+2 = 4
封闭区域：3
V（G） = 封闭区域+1 = 4

(2019年下半年软件设计师上午试卷29题)下图采用McCabe度量计算该程序图的环路复杂性为（）

A.3   B.4   C.5   D.6

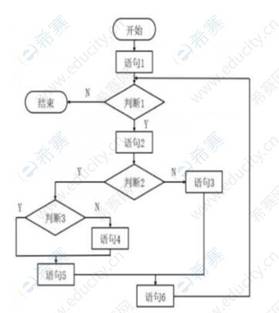
补全节点和有向弧

有向弧数：16
节点数：14
V（G） = 有向弧数-节点数+2 = 3
封闭区域：3
V（G） = 封闭区域+1 = 4