40.矩阵中的最长递增路径

1.题目链接：

329. 矩阵中的最长递增路径 - 力扣（LeetCode）329. 矩阵中的最长递增路径 - 给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。 示例 1：[https://assets.leetcode.com/uploads/2021/01/05/grid1.jpg]输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]输出：4 解释：最长递增路径为 [1, 2, 6, 9]。示例 2：[https://assets.leetcode.com/uploads/2021/01/27/tmp-grid.jpg]输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]输出：4 解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。示例 3：输入：matrix = [[1]]输出：1 提示： * m == matrix.length * n == matrix[i].length * 1 <= m, n <= 200 * 0 <= matrix[i][j] <= 231 - 1https://leetcode.cn/problems/longest-increasing-path-in-a-matrix/description/2.题目描述：

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。​

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：​

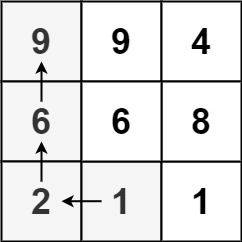
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]​
输出：4 ​
解释：最长递增路径为 [1, 2, 6, 9]。​
示例 2：​

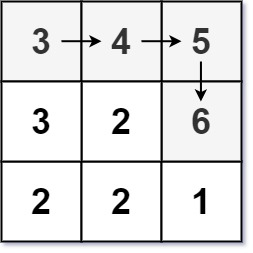
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]​
输出：4 ​
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。​示例 3：​
输入：matrix = [[1]]​
输出：1

     提示：
             m == matrix.length​
             n == matrix[i].length​
             1 <= m, n <= 200
             0 <= matrix[i][j] <= 2^31 - 1​
3. 解法（暴搜 -> 记忆化搜索 ）：​
算法思路：
暴搜：
a. 递归含义：给 dfs  一个使命，给他一个下标 [i, j] ，返回从这个位置开始的最长递增路径                      的长度；

b. 函数体：上下左右四个方向瞅一瞅，哪里能过去就过去，统计四个方向上的最大长度；​

c. 递归出口：因为我们是先判断再进入递归，因此没有出口~​

记忆化搜索：
a. 加上一个备忘录；
b. 每次进入递归的时候，去备忘录里面看看；​c. 每次返回的时候，将结果加入到备忘录里面。

Java算法代码：

class Solution {
    int m,n;
    int[] dx = {0,0,1,-1};
    int[] dy = {1,-1,0,0};
    int [][] memo;
    public int longestIncreasingPath(int[][] matrix) {
        m = matrix.length; n = matrix[0].length;
        memo = new int[m][n];
        int ret = 0;
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                ret = Math.max(ret,dfs(matrix,i,j));

        return ret;
    }
    public int dfs(int [][] matrix, int i, int j){
        if(memo[i][j] != 0)
            return memo[i][j];
        int ret = 1;
        for(int k =0; k < 4; k++){
            int x = i + dx[k], y = j + dy[k];
            if(x >= 0 && x < m && y>= 0 && y < n && matrix[x][y] > matrix[i][j] )
                ret = Math.max(ret,dfs(matrix,x,y) + 1);
        }
        memo[i][j] = ret;
        return ret;
    }
}

运行结果：

递归展开：

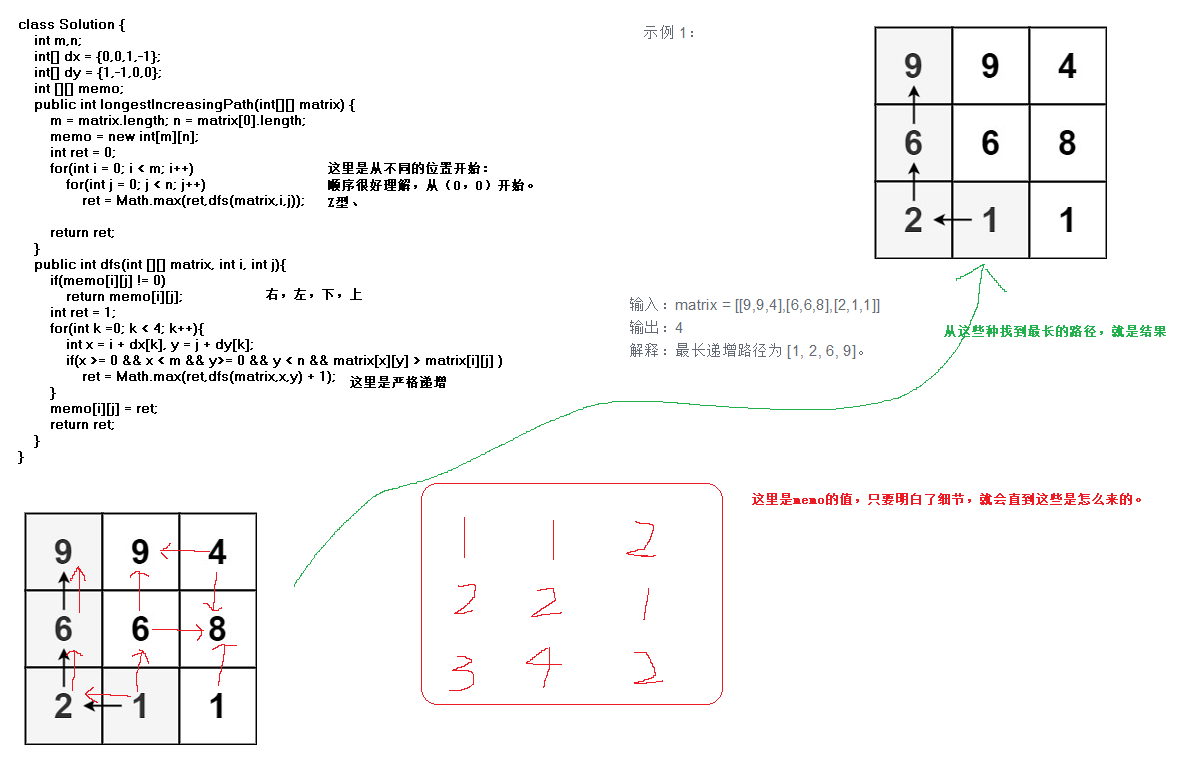
逻辑展开：掌握这道题的细节，比如，右，左，下，上的顺序。

Z型的顺序。

还有那个memo的记录（可以减少递归的次数）。