科研公式整理

一、 背景

为了更好的对公式有一个书写, 所以写了这样一个博客，便于更好的科研

二、 符号表示

2.1矩阵

$${\mathbf{W}}_2$$

2.2 所有行或者列

$\ast$表示所有行

2.3纬度

$C$,$S$

2.4 图表示

$\mathcal{G}(\mathcal{V},\mathcal{E})$，输入结点的特征表示为${\mathbf{x}}_v$, 对于$\forall v\in \mathcal{V}$

每层的循环$k=1,2,3,$ $\cdots$ $,K$
邻接结点的函数表示$\to$，$\forall u$ $\in$ $\mathcal{N}(v)$, 表示$v$的邻接结点。

2.5 函数表示

如果我们要去写一个聚合函数，可以表示为$\mathrm{A}\mathrm{G}\mathrm{G}\mathrm{R}\mathrm{E}\mathrm{G}\mathrm{A}\mathrm{T}{\mathrm{E}}_{\mathrm{k}}(\cdot )$可以用来表示为我们的一个函数。

2.6 实数表示

$\mathbf{R}$

2.7 实数向量

${\mathbf{R}}^n$

2.8对应元素相乘

$\odot$

2.9 积分表示

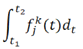
积分表示这一段时间的数量

2.10 对多个结果的拼接$\oplus$

2.11 内积

${\mathbf{x}}_i$

$<\cdot >$这个符号表示内积的符号

2.12 映射

$\to$

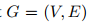
be a graph with $V$ the set of vertices.

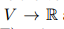
表示一个集合的映射。

2.13 变量

有本质区别,n维随机向量是一个向量,n维随机变量可以理解为一个n维数组,就是有n个元素

2.14 环境状态

环境$E$, 状态空间$X$, $x\in X$

2.15 奖赏

$Q(k)$表示记录$k$次的平均奖赏

2.16 分布

$\mathbf{d}\mathbf{d}\mathbf{i}\mathbf{s}$在dis前面加上个字母d表示分布上的

2.17 损失函数

$\mathcal{L}$表示损失函数

2.18 移动

${\mathcal{V}}_{S\to T}$表示像素移动域，从$S$到$T$

2.19

$\left(\begin{array}{c}T\\ k\end{array}\right)$ 表示从$T$个元素中取$k$个元素的组合数。

三、参考资料

https://blog.youkuaiyun.com/bqw18744018044/article/details/104948578