QUARTERNION RECURRENT NEURAL NETWORKS_quaternion networks.-优快云博客

文章来源：
Parcollet T, Ravanelli M, Morchid M, et al. Quaternion Recurrent Neural Networks[C]//International Conference on Learning Representations. 2018.
在四元数密集层(desne layer)中，所有参数都是四元数，包括输入、输出、权重和偏移。QRNN的方法是本文提出的，在全连接的推论过程中，使用了与普遍操作不同的定义过程，之前的可以理解为矩阵相乘，这里为四元数矩阵的哈密顿乘积（矩阵中的每一项是一个四元数）。
如果输入向量为 $N$ ，输出向量为 $M$ ，维度可以被划分为四个部分：第一个部分是 $r$ ，第二个部分是 $x_i$ ，第三个部分是 $y_j$ , 第四个部分是 $z_k$ 。四元数被表示为：
$Q=r1+xi+yj+zkQ=r1+x_\mathbf{i}+y_\mathbf{j}+z_\mathbf{k}$
四元数的共轭表示为：
$Q=r1−xi−yj−zkQ=r1-x_\mathbf{i}-y_\mathbf{j}-z_\mathbf{k}$
两种方法以矩阵方式表示四元数。第一种是通过二阶复数矩阵。第二种是以四阶实数矩阵表示四元数：
$Q_{\text {mat}}=\left[\begin{array}{cccc} r & -x & -y & -z \\ x & r & -z & y \\ y & z & r & -x \\ z & -y & x & r \end{array}\right]$
标准化的四元数表示为：
$Q◃=Qr2+x2+y2+z2Q^\triangleleft = \frac{Q}{{\sqrt {{r^2} + {x^2} + {y^2} + {z^2}} }}$
两个四元数的哈密顿积表示为：
$\begin{aligned} Q_{1} \otimes Q_{2}=&\left(r_{1} r_{2}-x_{1} x_{2}-y_{1} y_{2}-z_{1} z_{2}\right)+\left(r_{1} x_{2}+x_{1} r_{2}+y_{1} z_{2}-z_{1} y_{2}\right) \boldsymbol{i}+\\ &\left(r_{1} y_{2}-x_{1} z_{2}+y_{1} r_{2}+z_{1} x_{2}\right) \boldsymbol{j}+\left(r_{1} z_{2}+x_{1} y_{2}-y_{1} x_{2}+z_{1} r_{2}\right) \boldsymbol{k} \end{aligned}$
输入是一个四元数，输出是一个四元数，权重是四元数，偏置也是四元数
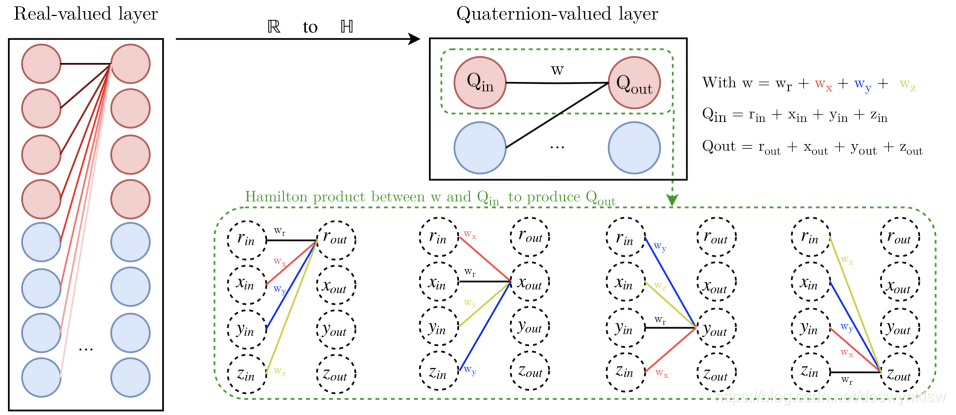
在这里插入图片描述
四元数有三个虚部，并且 $i2=j2=k2=ijk\mathbf{i}^2=\mathbf{j}^2=\mathbf{k}^2=\mathbf{ijk}$
依据RNN的前向传播（注意拼接和加）表示为，
$h_{t}=\alpha\left(W_{h h} h_{t-1}+W_{h x} x_{t}+b_{h}\right)$
四元数的前向传播表示为：
$h_{t}=\alpha\left(W_{h h} \otimes h_{t-1}+W_{h x} \otimes x_{t}+b_{h}\right)$
一个四元数的激活函数表示为：
$\alpha(Q)=f(r)+f(x) \mathbf{i}+f(y) \mathbf{j}+f(z) \mathbf{k}$
$f(⋅)f(\cdot)$ 是一个标准的激活函数。