二分查找算法

算法笔记–二分查找

二分查找是对有序序列查找的一种高效方法，时间复杂度为 log2(n)，它的核心思想是分而治之，逐渐细化，最终匹配结果。

看图理解

• 首先将数组对半分，判断目标值是在mid的左边，或者右边，或者等于mid值

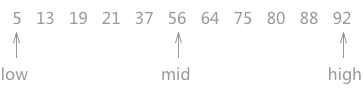
• 进一步细化，并采用同样的判断

• 重复步骤，直至mid的值等于目标的值

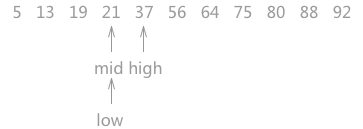
案例实践

public class BinarySearch {
    public static void main(String[] args) {
        int[] a = {1,2,3,4,5,6,7,8,9};
        System.out.println("递归二分查找结果： " + search(a, 6));
        System.out.println("不使用递归二分查找结果： " + search2(a, 0, a.length - 1 , 6));
    }

    private static int search(int[] arr, int search){
        int n = arr.length;
        return search(arr,0,n - 1, search);
    }

    /**
     * @param arr
     * @param left    左边索引
     * @param right   右边索引
     * @param findVal 要查找的值
     * @return 未找到返回 -1，否则返回该值的索引
     */
    private static int search(int[] arr, int left, int right, int findVal) {
        // 当找不到时，则返回 -1
        if (left > right) {
            return -1;
        }
        int mid = (left + right) / 2;
        int midVal = arr[mid];
        // 相等则找到
        if (midVal == findVal) {
            return mid;
        }
        // 要查找的值在右边，则右递归
        if (findVal > midVal) {
            // mid 的值，就是当前对比的值，所以不需要判定
            return search(arr, mid + 1, right, findVal);
        }
        return search(arr, left, mid - 1, findVal);
    }


    /**
     * 不使用递归
     * @param arr
     * @param left
     * @param right
     * @param findVal
     * @return
     */
    private static int search2(int[] arr,int left,int right,int findVal)
    {
        while(left < right)
        {
            int mid = (left + right) / 2;
            if(arr[mid] < findVal){
                left = mid+1;
            }else {
                right = mid;    //一直让arr[right]>=findVal,最后剩下一个即为我们所要的解.
            }
        }
        return arr[right] == findVal ? right : -1;
    }
}