归并排序算法

算法笔记–归并排序

归并排序一种有效、稳定的排序算法，其核心思想是分治思想，通过递归调用实现排序。归并排序的时间复杂度为 O(nlogn)，适用于数据量大，并且对稳定性有要求的场景。

看图理解

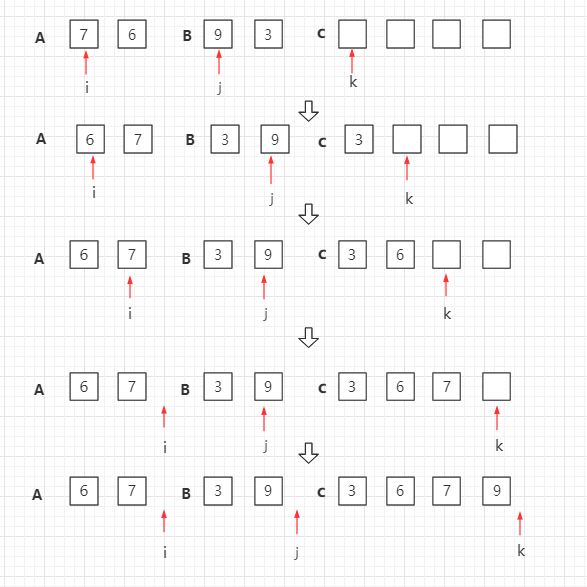
• 核心排序，分而治之，引用了另一数组进行数据暂存，双指针引索引推进，实现两个无序数组排序

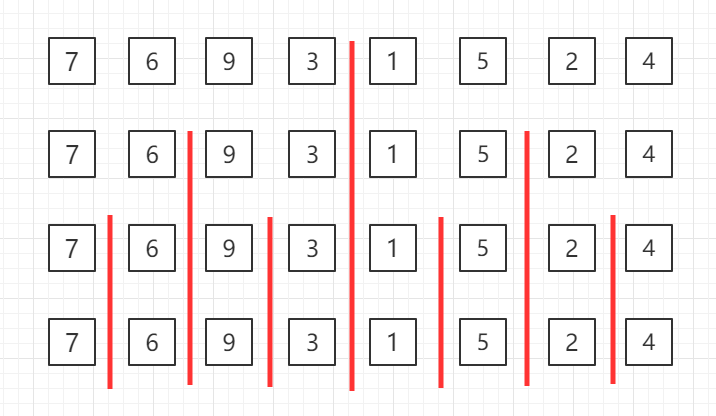
• 递归思想，分组，由小到大进行排序

• 对第三行两个一组的数据进行归并排序

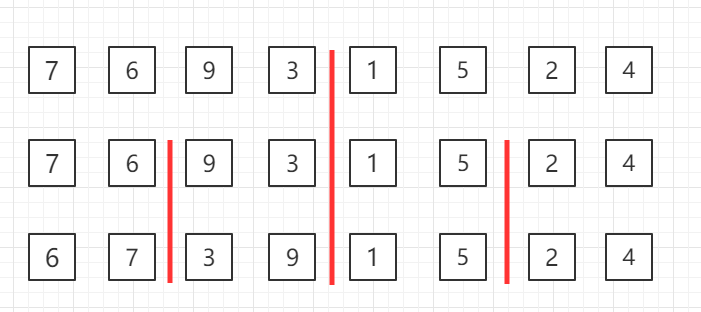
• 对第二行四个一组的数据进行归并排序

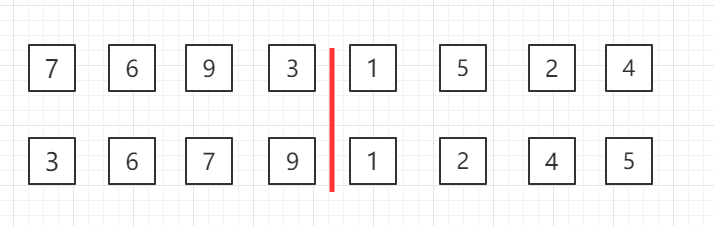
• 整体进行归并排序

  

• 动图描述整个过程

  

解题：用一个数组来表示元素集合

1. 二分数组，分为左右子数组
2. 子数组按核心排序合并
3. 递归调用循环

案例实践

public class MergeSort {

    public static void main(String[] args) {
        int[] a = {5,6,1,2,3,4,7,8,9};
        sort(a);
        for (int i = 0; i < a.length; i++) {
            System.out.printf("%2d",a[i]);
        }
    }

    private static void sort(int[] arr){
        int n = arr.length;
        sort(arr, 0, n - 1);
    }

    /**
     * 递归调用
     * @param arr
     * @param left
     * @param right
     */
    private static void sort(int[] arr, int left, int right){
        if (left >= right) {
            return;
        }
        int mid = (left + right) / 2;
        sort(arr, left, mid);
        sort(arr, mid + 1, right);
        // 对于arr[mid] <= arr[mid+1]的情况,不进行merge
        // 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
        if (arr[mid] > arr[mid + 1]){
            merge(arr, left, mid, right);
        }
    }

    /**
     * 排序合并
     * @param arr
     * @param left
     * @param mid
     * @param right
     */
    private static void merge(int[] arr, int left, int mid, int right){
        //注意这里的深拷贝，不能是对象的引用
        int[] temp = arr.clone();
        int i = left, j = mid + 1;
        int index = left;
        while(i <= mid || j <= right){
            if(i > mid){ // 如果左半部分元素已经全部处理完毕
                arr[index++] = temp[j];
                j++;
            }else if(j > right){  // 如果右半部分元素已经全部处理完毕
                arr[index++] = temp[i];
                i++;
            }else if(temp[i] < temp[j]){ // 左半部分所指元素 < 右半部分所指元素
                arr[index++] = temp[i];
                i++;
            }else{ // 左半部分所指元素 >= 右半部分所指元素
                arr[index++] = temp[j];
                j++;
            }
        }
    }

    private static void printArr(int[] arr){
        for (int k = 0; k < arr.length; k++) {
            System.out.printf("%2d",arr[k]);
        }
    }
}