数组中的逆序对

1.暴力两层for循环，时间复杂度$O(n^2)$,空间复杂度$1$.

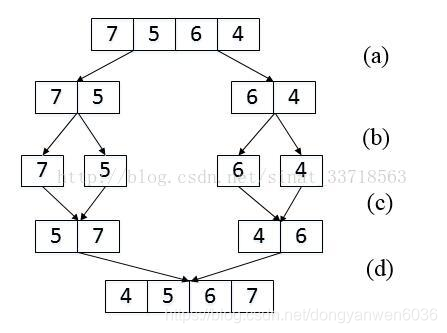
2.归并排序时间复杂度$O(nlogn)$，空间复杂度$n$.

分析：
交换copy和data是因为：
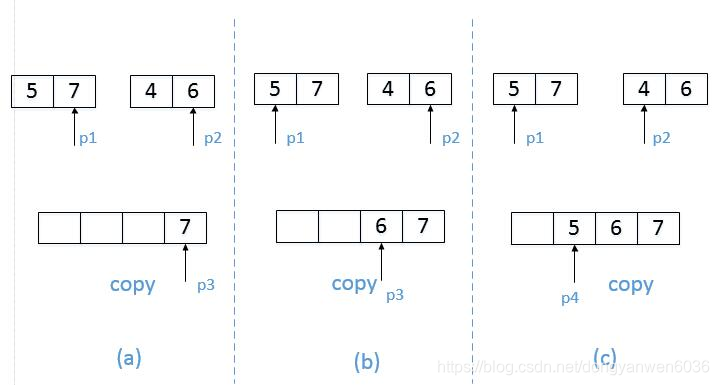
1.在每次的操作中，数值的比较都是采用当前传入函数中第一项，也就是data；比较的结果都存放到copy中；也就意味着此时copy中是经过此次调用的结果。
2.从最底层返回时，进入了(start == end)的情形，data 和 copy 完全没有修改，此时copy和data还是一样的。
3.进入倒数第二层时，程序进入上图26行以后部分，copy是部分排序后的新数组，data是旧数组。注意这里都是传值的调用，数组都是直接修改的。
倒数第二层使用的copy其实是倒数第三层中的data,这就确保了倒数第三层进入26行以后时，数据比较使用的data是最新排序的数组。
4. 倒数第三层将排序的结果存入copy中。程序在倒数第四层进入26行后，使用的data数组为刚刚倒数第三层中的最新排序的copy.
5. 也就是说，在每次程序进入26行时，此时的data是最新的排序结果，copy是次新的结果。
在最后一次进入26行以后时，copy为完整排序后的结果，data是次新的结果。
然而这里第一个类内函数调用第二个函数时，data和copy的顺序没有改变，所以最后结果应该copy是完整排序的结果.data是差一步完成排序的结果。以输入[7,5,6,4], 最后的结果copy[4,5,6,7], data[5,7,4,6].

class Solution {
public:
	long long InversePairsCore(vector<int>&data, vector<int>&copy, int low, int high)
	{
		if (low == high)
		{
			copy[low] = data[low];
			return 0;
		}
		int len = (high - low) / 2;
		long long left = InversePairsCore(copy, data, low, low + len);
		long long right = InversePairsCore(copy, data, low + len + 1, high);
		//两指针尾端
		int i =low+len , j = high;
		int indexcopy = high;
		long long count = 0;
		while (i>=low&&j>=low+len+1)
		{
			if (data[i] > data[j])
			{
				copy[indexcopy--] = data[i--];
				count += j - low - len;
			}
			else
			{
				copy[indexcopy--] = data[j--];
			}
		}
		for (; i >= low; i--)
			copy[indexcopy--] = data[i];
		for (; j >= low + len + 1; j--)
			copy[indexcopy--] = data[j];
		return left + right + count;
    }
	int InversePairs(vector<int> data) {
		int len = data.size();
		if (len <= 0)return 0;
		vector<int> copy;
		for (int i = 0; i < len; i++)
			copy.push_back(data[i]);
		long long count = InversePairsCore(data,copy,0,len-1);
		return count % 1000000007;
	}
};

参考剑指offer