大家好啊,我是董董灿。
在你刚学习神经网络的时候,有没有被一个名字叫做“交叉熵”的概念绕的云里雾里,以至于现在看到这个概念,依然很懵。
今天就来看一下,这个所谓的“交叉熵”到底是什么,以及它在神经网络扮演什么角色,神经网络中为什么要用它来做损失函数?
本篇文章前半部分会有一些公式的推导和解释(参考Naoki大佬博客,感兴趣可查看英文原文:https://naokishibuya.medium.com/demystifying-cross-entropy-e80e3ad54a8),你也可以直接跳到最后一部分查看神经网络中交叉熵损失的介绍。

1、交叉熵
“交叉熵”包含了“交叉”和“熵”这两部分,如果把这两部分都理解透彻,那这个概念也就没有什么神秘可言了。
“熵”在之前的一篇文章中已经说过了,如果对熵还不清楚的同学,可以看下这篇文章——对“熵”一知半解?带你揭开“熵”的神秘面纱。
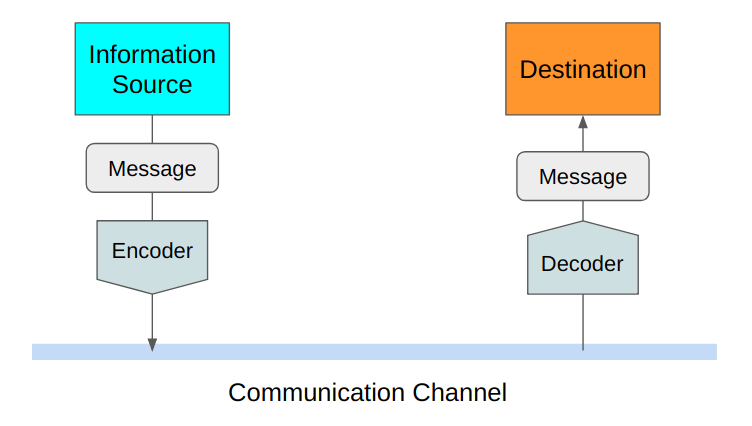
总的来说,大科学家香农大佬,定义了熵来计算“在确保信息传递过程不失真的情况下,传递信息所需要的最小编码大小”。
说的好理解一些,就是我向你传递一个消息,在确保没有任何信息丢失的情况下,我需要用到的最小的信息量。
在知道了熵的概念之后,下面从公式的角度一点点抽丝剥茧,来说明交叉熵。
对于存在概率分布的事件,计算熵的公式如下,这个公式在上篇文章解密熵中详细论述过:
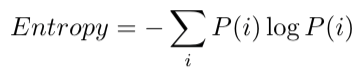
其中,i 为发生的离散事件,根据不同的场景 i 会代表不同的含义,比如之前举的例子,东京的天气是阴天还是晴天,就属于在一天中会发生的离散事件。P(i)为发生这些事件的概率,对应到天气便是某一天降雨的概率,晴天的概率等。
上式熵的公式我们稍微变一下型,将负号和 log(P(i)) 看做一个变量,由于P(i)是每个事件 i 发生的概率,那么上式便可以理解为离散事件 i 发生概率的负对数(-log(p(i))的平均值(也叫期望)。
因此,熵的计算公式,便有了一个期望形式:

其中,x~P 表示用事件 x 服从概率分布 P,并且使用 P 来计算期望,同时熵一般用字母 H 表示,于是熵的公式可以写成如下形式:

简单点讲,熵这一概念,是用来表征在遵循特定概率分布的事件事件 x 发生时,传递信息需要用到的理论平均最小编码大小。
因此,只要我们知道发生事件的概率分布,我们就可以计算它的熵,如果我们不知道它的概率分布,那就没有办法计算熵。
所以,对于不知道概率分布的事件,需要想办法来估计概率分布,从而计算熵。
而利用估计的概率分布来计算熵,得到的是估计熵,这一点很重要,对我们接下来理解交叉熵很有帮助。
2、计算估计熵
假设现在向纽约发送东京的天气情况,并且希望在发送信息的过程中,将天气信息编码到最小来发送。
但我们遇到一个问题,那就是东京的天气我并不能百分百确定,也就是说天气在发生之前,我是不知道的,我所知道的,仅仅能通过天气预报的形式估计出一个天气概率。
假设在观察了东京一段时间的天气后,我大概得到了一个天气的概率分布Q,那么使用这个估计的概率分布Q,便可以计算出一个熵值(此时称为估计熵Estimated Entropy)为:

如果 Q 非常接近真实发生的概率分布,那么上式计算的结果(估计熵)便能更精确的反应传递信息需要的最小编码大小。
但是,这种计算估计熵的公式,存在两种不确定性。
首先,x~Q 表示我们利用概率分布 Q 来计算期望,而 Q 是估计出来的,可能会与实际概率分布 P 相差很大。
其次,计算最小编码时,是基于估计的 Q 来计算的概率分布的负对数 -log(Q),而这也不会是100%准确的。
由此可见,Q 即影响期望,又影响最小编码估计,因此,计算出的估计熵并不能反应出什么,继而将估计熵和真实熵进行对比,也无法得出什么有意义的结论。
那怎么办呢?先回到这件事的本质上,其实一开始我们关心的,是在传递信息的时候,如何让编码大小尽可能小,也就是传递的信息量最小。
因此,我们既然有了熵的理论了,可以基于熵的理论,将我们的计算的编码大小与理论最小的编码进行比较即可,而不去考虑期望,将Q的影响由双变量变为单变量。
举个例子,假设在观察一段已发生的东京天气后,得到了天气发生的真实分布P ,我们可以使用概率分布 P 来计算真实的平均编码大小,而利用天气预报中的概率分布 Q,来计算未发生的事件所需要的编码大小。
这便是基于概率事件 P 和 Q 之间的交叉熵:
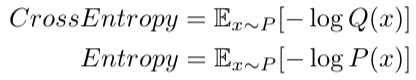
上式中,计算期望我们使用了相同的真实概率分布 P,因此此时比较两个熵的大小,实际上比较的是 -logQ 和 -logP 的大小,也就是理论最小编码和实际编码大小。
说的通俗一点,交叉熵在交叉的检查编码大小,这就是交叉熵中“交叉”的意思。
3、交叉熵 ≥ 熵
通常,交叉熵用H表示如下:
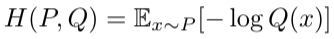
H(P, Q) 表示使用 P 计算期望,使用 Q 计算编码大小。
因此,H(P, Q) 和 H(Q, P) 不一定相同,但如果 Q=P,在这种情况下H(P, Q) = H(P, P) = H(P)并且变成熵本身。
有一点需要注意的事,在计算期望时应该使用真实概率P,因为它反映了真实事件的分布。而在计算编码大小时应该使用Q,因为它反映了对消息进行编码的大小。
可以看到,如果估计的概率分布是完美的,也就说如果估计的概率分布 Q 刚好等于 P,那么此时 H(P, Q)=H(P),否则 H(P, Q) > H(P)。
以上便是交叉熵和熵之间的联系,不知各位同学看懂了没,没看懂没关系,接着看下下面的实例,或许你会对交叉熵有更深刻的理解。
4、交叉熵作为损失函数
假设有一个动物图像数据集,其中有五种不同的动物,每张图像中只有一只动物。

来源:https: //www.freeimages.com/
我们将每张图像都使用 one-hot 编码来标记动物。对one-hot编码不清楚的可以移步这里有个你肯定能理解的one-hot。

上图是对动物分类进行编码后的表格,我们可以将一个one-hot编码视为每个图像的概率分布。
第一个图像是狗的概率分布是 1.0 (100%)。
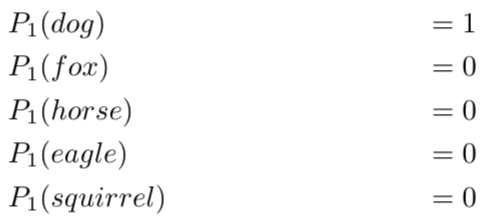
对于第二张图是狐狸的概率分布是1.0(100%)。

以此类推,此时,每个图像的熵都为零。

换句话说,one-hot 编码标签 100% 确定地告诉我们每张图像有哪些动物:第一张图片不可能 90% 是狗,10% 是猫,因为它100%是狗。
现在,假设有一个神经网络模型来对这些图像进行分类,在神经网络执行完一次推理,或者完成一轮训练迭代后,它可能会对第一张图像(狗)进行如下分类:

该分类表明,第一张图像中狗占 40%,狐狸占 30%,马占 5%,老鹰占 5%,松鼠占 20%。
但是,单从图像标签上看,它100%是一只狗,标签为我们提供了这张图片的准确的概率分布。

那么,此时模型分类预测的效果如何呢?我们可以计算利用标签的one-hot编码作为真实概率分布 P,模型预测的结果作为 Q 来计算交叉熵:

结果明显高于标签的零熵,说明预测结果并不是很好。
先不急,继续看另一个例子。
假设模型经过了改良,在完成一次推理或者一轮训练后,对第一张图得到了如下的预测,也就是说这张图有98%的概率是狗,这个标签的100%已经差的很少了。

我们依然计算交叉熵:

可以看到交叉熵变得很低,随着预测变得越来越准确,交叉熵会下降,如果预测是完美的,它就会变为零。
基于此理论,很多分类模型利用交叉熵作为模型的损失函数。
在机器学习中,由于多种原因(比如更容易计算导数),对数的计算大部分情况下是使用基数 e 而不是基数 2 ,对数底的改变不会引起任何问题,因为它只改变幅度。
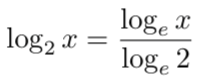






















 226
226

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










