一个简单的选择排序

一、选择排序算法

选择排序算法是一种简单直观的排序算法。其基本思想是在未排序序列中找到最小元素，存放到排序序列的起始位置，然后再从剩余未排序元素中继续寻找最小元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

以下是选择排序算法的一些要点：

1. 时间复杂度：选择排序的时间复杂度为O(n^2)，其中n是待排序元素的数量。在最坏情况下，即每次选取的最小元素都在最后一个位置，选择排序的时间复杂度达到O(n^2)。
2. 空间复杂度：选择排序的空间复杂度为O(1)，这意味着它只需要常数级别的额外空间，而不需要像归并排序或快速排序那样使用额外的O(n)空间。
3. 稳定性：选择排序是稳定的排序算法，这意味着相等的元素在排序后保持其原始的相对顺序。
4. 应用场景：尽管选择排序在处理大量数据时的效率不如其他一些高级排序算法，但在某些情况下仍然是一个不错的选择。例如，当数据量较小，或者当内存限制使得使用其他算法不切实际时，选择排序可以发挥出其简单高效的优势。
5. 改进与优化：尽管选择排序的基础版本效率不高，但可以通过一些改进来提高其性能。例如，可以使用二分查找法来改进选择排序，使其在最坏情况下的时间复杂度降低到O(nlogn)。

二、代码实现

package zhoumo.java.simple;

import java.util.Arrays;

public class Zhoumo {
 public static void main(String[] args) {
  //选择排序
  
  int []a={21,43,54,28,39,24};
  int temp;
   Arrays.sort(a);
   for (int i = 0; i < a.length; i++) {
   
   for (int j = i+1; j < a.length; j++) {
    if(a[i]>a[j]){
     temp=a[i];
     a[i]=a[j];
     a[j]=temp;
      
    }
    
    
   }
   System.out.print(a[i]+"  ");
  }
  
   System.out.println("hello");
  
 }
 

}

package zhoumo.java.simple;

import java.util.Arrays;

public class Zhoumo {
 public static void main(String[] args) {
  //选择排序
  
  int []a={21,43,54,28,39,24};
  int temp;
   Arrays.sort(a);
   for (int i = 0; i < a.length; i++) {
   
   for (int j = i+1; j < a.length; j++) {
    if(a[i]>a[j]){
     temp=a[i];
     a[i]=a[j];
     a[j]=temp;
      
    }
    
    
   }
   System.out.print(a[i]+"  ");
  }
  
   System.out.println("hello");
  
 }


}

三、排序算法总结

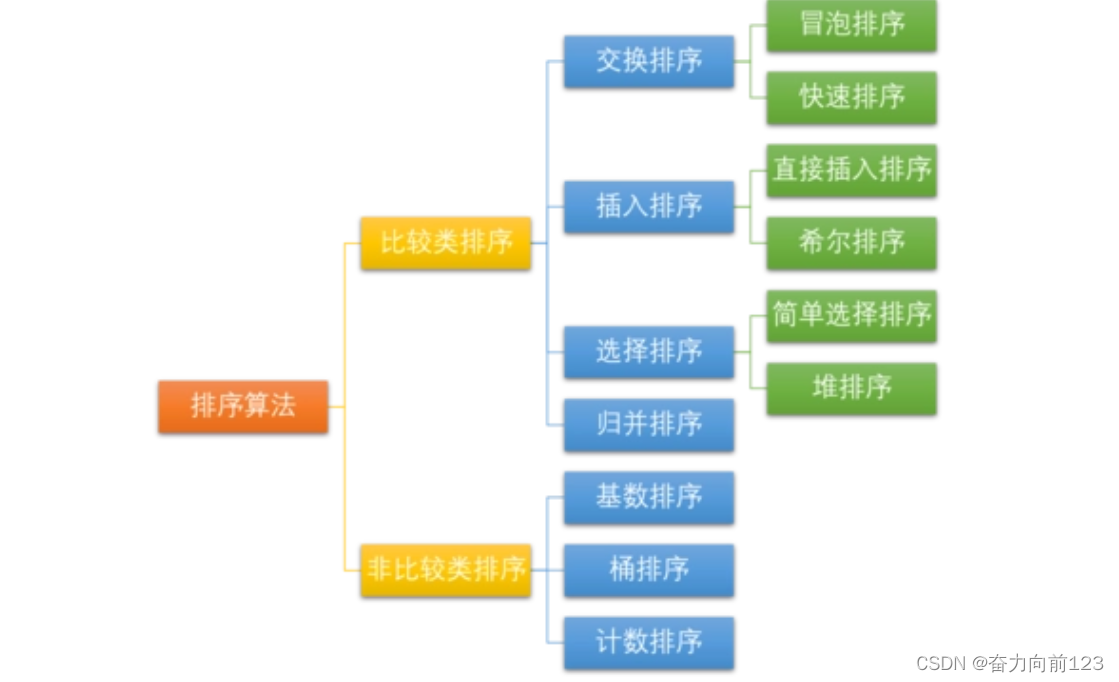
Java中提供了多种排序算法，这些算法主要在java.util.Arrays和java.util.Collections这两个类中。以下是这些排序算法的简单总结：

1. 冒泡排序（Bubble Sort）

   • 原理：重复地遍历待排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。
   • 优缺点：简单易懂，但效率低。

2. 选择排序（Selection Sort）

   • 原理：在未排序序列中找到最小（或最大）元素，存放到排序序列的起始位置，然后再从剩余未排序元素中继续寻找最小（或最大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
   • 优缺点：简单易懂，但效率低。

3. 插入排序（Insertion Sort）

   • 原理：将一个数据插入到已经排好序的有序数据中，从而得到一个新的、个数加一的有序数据。
   • 优缺点：简单易懂，但效率低。

4. 快速排序（Quick Sort）

   • 原理：使用分治法策略，选取一个基准元素，重新排列数组，使得基准元素的左侧都比它小，右侧都比它大。然后对基准元素的左侧和右侧分别递归进行这个过程。
   • 优缺点：平均时间复杂度为O(nlogn)，但在最坏的情况下（输入的数据是逆序的）时间复杂度为O(n²)。

5. 归并排序（Merge Sort）

   • 原理：采用分治法，将两个已经排序的数列合并成一个新的、有序的数列。
   • 优缺点：稳定、时间复杂度为O(nlogn)、空间复杂度为O(n)。

6. 堆排序（Heap Sort）

   • 原理：将一个无序数组构建成一个大顶堆或小顶堆，然后将堆顶元素（最大值或最小值）与堆尾元素互换，之后将剩余元素重新调整为大顶堆或小顶堆（取决于交换前的堆属性），以此类推，直到整个数组有序。
   • 优缺点：稳定、时间复杂度为O(nlogn)、空间复杂度为O(1)。

7. 希尔排序（Shell Sort）

   • 原理：是插入排序的一种更高效的改进版本（通过比较相距一定间隔的元素），也称为“缩小增量排序”。希尔排序是非稳定排序算法。
   • 优缺点：希尔排序的时间复杂度依赖于增量序列的选择，最坏情况仍然是O(n²)。

8. 桶排序（Bucket Sort）

   • 原理：把数据分成几个桶，每个桶内部进行排序，然后对所有桶的排好序的数据进行一次合并操作。
   • 优缺点：适用于数据范围比较大且数据分布均匀的情况。时间复杂度取决于桶的数量和每个桶内数据的排序方式。空间复杂度为O(n)。

9. 计数排序（Counting Sort）

   • 原理：计数排序是一种线性时间复杂度的排序算法，适用于正整数数组。它的工作原理是统计数组中每个元素出现的次数，对每个元素按照其值的大小进行分类和计数，然后按照计数的顺序进行排序。
   • 优缺点：计数排序的时间复杂度为O(n)，但要求输入数据必须在一定范围内且每个数据的取值尽量均匀分布。计数排序是一种稳定的排序算法。

10. 基数排序（Radix Sort）

    • 原理：基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（如名字或日期）和特定格式的浮点数，基数排序并不是只能用于整数。
    • 优缺点：稳定、时间复杂度为O(nklogk)，其中k是数字的位数。空间复杂度为O(n)。

11. 双指针排序（Two-Pointer Sort）

    • 原理：双指针排序是指通过两个指针分别指向待比较的两个元素，然后交换两个指针指向的元素的位置，直到两个指针相遇或交错为止。常见的双指针排序算法有冒泡排序和插入排序等。
    • 优缺点：双指针排序算法简单易懂，但时间复杂度可能较高，如冒泡排序在最坏情况下的时间复杂度为O