要求: 输入一个二维整形数组,数组里有正数也有负数。
二维数组中连续的一个子矩阵组成一个子数组,每个子数组都有一个和。
要求所有子数组的和的最大值。要求时间复杂度为O(n)。
#include<iostream> using namespace std; void main () { int x,y,i,j,m=0,A[100][100]; cout<<"输入矩阵的行()和列"; cin>>x>>y; if(x>100||y>100) { cout<<"请重新输入:"; cin>>x>>y; } for(i=0;i<x;i++) { for(j=0;j<y;j++) { cin>>A[i][j]; } } int sum[100]={0},max=0,result=A[0][0]; for(i=0;i<x;i++)//确定子数组的最大上界(为第i行) { while(m+i<x)//确定子数组有m+i行 { //把子数组当成一位数组一样,求最大子数组的和 for(j=0;j<y;j++) { sum[j]=sum[j]+A[m+i][j]; } max=0; for(j=0;j<y;j++) { if(max+sum[j]>sum[j]) { max=max+sum[j]; } else { max=sum[j]; } if(max>result) { result=max; } } m++;//是子数组的行数+1 } //初始化m和sum[]的值,使子数组最大上界下降1,之后重新循环。 m=0; for(j=0;j<y;j++) { sum[j]=0; } } cout<<result; }
思路:对前几天所做的返回一维数组中最大子数组的和进行改进,二维数组求最大子数组是从一维数组扩展而来,只是多了一个变量,同时定义两个变量,分析变量的范围,然后从第一行开始确定最大子数组范围,把最大子数组分成若干行,再用一维数组求子数组之和最大值的方法。依次求出最大值,依次比较,保留最大的。
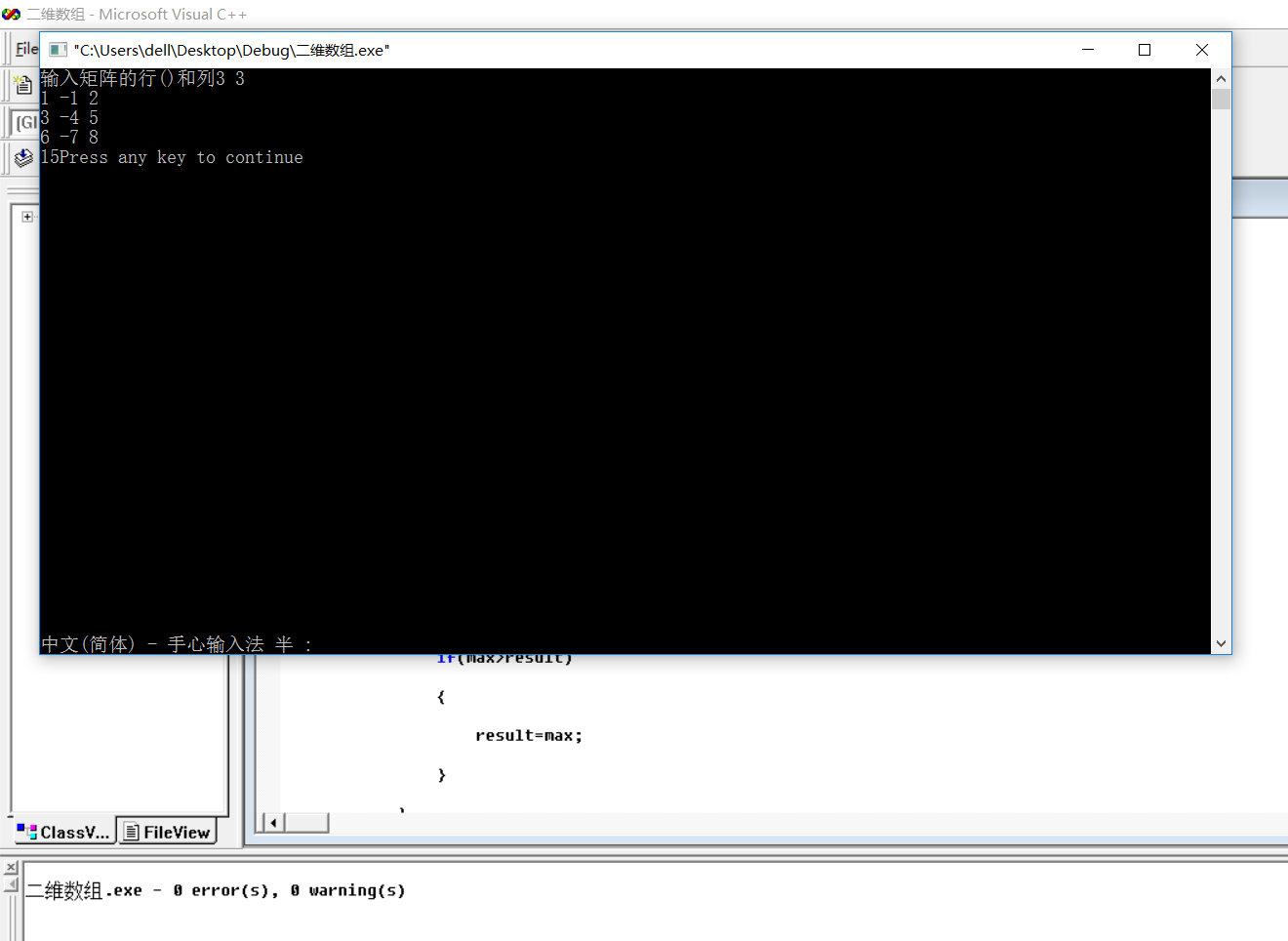




 本文介绍了一种求解二维数组中最大子矩阵和的算法,通过将问题转化为一维数组最大子数组和的问题,实现了O(n)的时间复杂度。文章详细解释了算法的实现过程,并提供了完整的代码示例。
本文介绍了一种求解二维数组中最大子矩阵和的算法,通过将问题转化为一维数组最大子数组和的问题,实现了O(n)的时间复杂度。文章详细解释了算法的实现过程,并提供了完整的代码示例。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








