RL an introduction学习笔记(1)：Muti-arm Bandits

Blog中的代码参考了Reinforcement learning an introduction的实例代码，Github地址如下：
ShangtongZhang/reinforcement-learning-an-introduction

1. 从问题入手：

1.1 问题描述：Muti-arm Bandits

Muti-armed Bandits（多臂老虎机）问题，也叫K-armed Bandit Problem。
参数K表示当前游戏厅中有K台老虎机可供你选择，且游戏厅里的这K台老虎机的真实价值（true value）各不相同。
举一个栗子：
你拿着100块钱入场，只玩1号机，可能在你进行无数次投币摇奖后你的资产变成了-20块(找老板赊了账)，但是如果你玩2号机，可能你的资产在进行无数轮游戏后变成了180块。
这里强调的是，我们在一开始无法得知每台老虎机能带给我们的收益。在没有进行无数轮游戏之前，我们无法得知每台老虎机的真实价值（true value）。

游戏流程如下：

现在，你作为agent，参与N轮游戏，每轮游戏中你将依据历史信息（eg：在每台老虎机上的收益统计信息）在K个老虎机中选择一个摇奖，老虎机将依据概率分布，给予回报（return）。

你的游戏目标是：

maximize the expected total reward over some time period, for example, over 1000 action selections, or time steps.

在进行n轮游戏（time steps）过程中，找出最佳的老虎机（或者称找出最佳的策略， 或者称做出最好的选择），使得最终收益最大化

1.2 问题简化：10-armed testbed

为了探寻问题的解决算法，我们简化了原题目，将k-armed bandits 简化为10-armed testbed：

1. 总共进行2000轮游戏；
2. 每轮游戏进行1000次选择（1000 time steps）；
3. 每次共有10台老虎机可供选择，用字母A_t（action）表示在第t轮游戏时选择的老虎机；
4. 每台老虎机的真值（true value, q*(a)）由均值为0，方差为1的高斯分布（normal distribution）给出；
5. 每台老虎机的回报（R_t）由均值为该动作真实价值（q*(a)），方差为1的高斯分布决定，如下图所示；
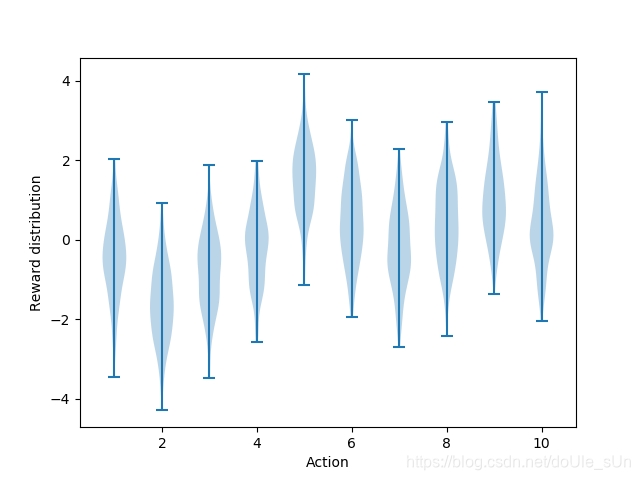
   代码：

plt.violinplot(dataset=np.random.randn(200,10) + np.random.randn(10))

5. 由于不知道每个选择（action）的真实价值（q*(a)）谁高谁低，我们需要对动作价值（action-value）进行评估（estimate），对每个动作的评估价值记作：Q_t(a)，t代表第t轮游戏，a代表动作，即在t时刻选择的老虎机；

显然，我们的目标是尽量使得我们对10台老虎机的估计值Q_t(a)随着t的增加（即：随着游戏的进行），逐渐收敛到q*(a)，与此同时，我们的最终收益（reward）也能最大化。

1.3 执行流程：The Code

基于上述简化后的游戏规则，我们可以写出游戏运行的框架，如下所示。

• q_true是一个1*10的列表，记录每个老虎机的真实价值（true value）
• q_estimate是一个1*10的列表，记录agent对每一个老虎机价值的估计值
• act()方法是依据算法（我们稍后会探讨这部分内容）选择合适的行动（即选择几号老虎机）
• step(action)是agent选择action后执行该action，环境（即老虎机）给予奖励reward
• rewards二维数组即我们的小本本，记录历史信息，用于结束2000轮游戏后，观察游戏运行过程中的数据

# 2000轮游戏
for game in range(2000):
	# 每轮游戏前初始化每台老虎机的真实价值
    q_true = np.random.normal(0, 1, 10)
    q_estimate = np.zeros(10)
	
	# 每轮游戏进行1000次选择
    for time_step in range(1000):
        # 根据policy选择action
        action = act()
        # 环境（即老虎机）依据action给予回报reward
        reward = step(action)
        # 记在总收益的本子上，第game轮游戏的第time-step次选择，得到的回报是reward
        rewards[game][time_step] = reward

2. 解决方案：

最新一版的书中提出了四种解决这个问题的方法，分别是Greedy算法，Epsilon-greedy算法，UCB（Upper-Confidence-Bound）算法，Stochastic Gradient Ascent算法

2.1 算法引入：sample-average method

由于agent无法得知每个action的true value，为了最大化最终收益，我们可以对action的价值进行评估，我们可以多次选择同一个action，并统计平均该action的reward作为该action的估计值，记作Q_t(a)。而后，依据该估计值和其它的相关信息进行决策。

2.1.1 符号表示

• action value的估计值Q_t(a)：
  
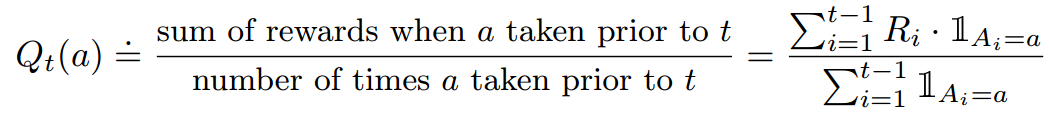
• 在t时刻agent选择的行动A_t：
  
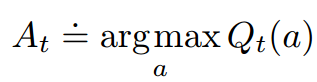
  注意，Q_t和A_t公式中的符号和“=”不太一样：
  

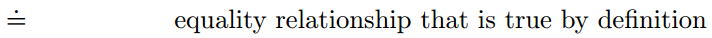
2.1.2 算法思想

与数理统计里的大数定律概念一样，当游戏执行无数轮以后，显然我们的动作评估值Q_t(a)与action的true value，q*(a)相差无几。更严谨的说法是，

当t趋近于无穷大时，Q_t(a)收敛于q*(a)

2.1.3 探索(explore)与利用(exploit)

例如，你面前有10台老虎机，在你进行27轮游戏后，你依据统计信息知道，当前累计回报最高的是6号机，达到了0.6个币/每轮游戏，累计回报第二高的是8号机，其值为0.3个币/每轮游戏。
此时，虽然可能其它的老虎机的真实价值最高，但是稳妥的你决定依据历史信息，选择6号机，最终6号机给你的回报是-0.6（真实值为-1），这叫做exploit。
倘若你爱挑战，选择了目前来说第二好的8号机。可能得到的回报就成了+0.9（真实值为1.3），这叫做explore。
此后，你将这轮的游戏信息记在小本本上，给6号机写个大大的low（或者给8号机写个大大的good），然后开始了下一轮游戏，继续进行选择。

2.2 Greedy算法

算法描述：

Greedy action selection always exploits current knowledge to maximize immediate reward; it spends no time at all sampling apparently inferior actions to see if they might really be better.

对应于10-armed-testbed 问题，则是每次选择Q_t(a)中最大的一项：

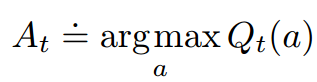
代码如下：

def act():
    q_best = np.max(q_estimate)
    # 有多个相同的最大值，则随机选择一个action
    return np.random.choice([action for action, q in enumerate(q_estimate) if q == q_best])

对2000轮游戏对应的每一个time step获得的reward求和取平均，即
$$AverageReward=\frac{1}{2000}\sum _{t=1}^{2000}Rewards[t][timestep]$$
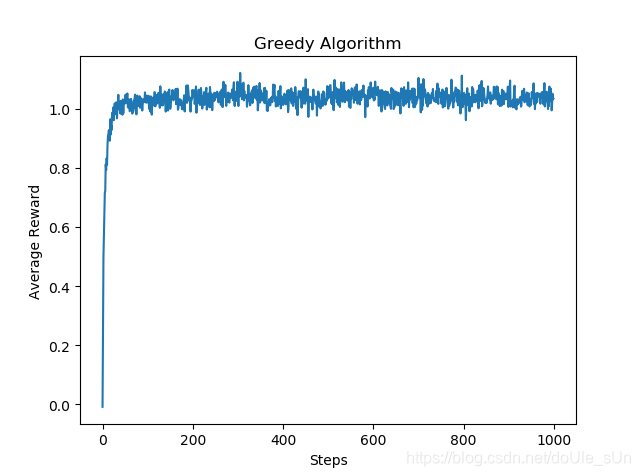
这表示的是agent在使用该算法进行游戏时，在每一次做出选择后获得的reward的估计值。可以看出在经过一些steps后，agent获得的reward基本不再变化，但仍然不愿意尝试其它选择：

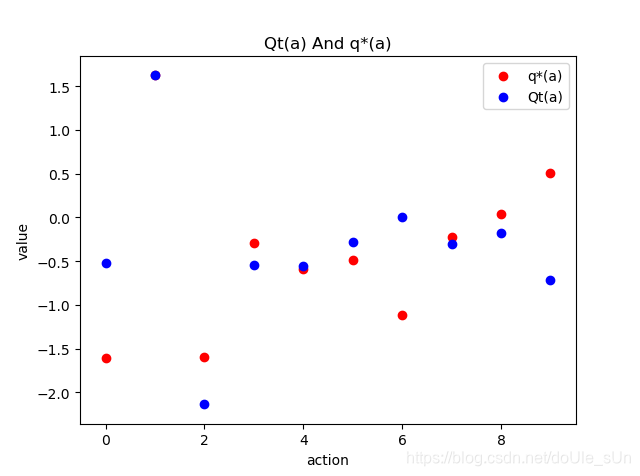
在进行1000次尝试之后，action评估值与其真实值的比较。显然，二者之间差距较大，该agent未能找到好的策略来找到action的真实价值：

2.3 Epsilon-Greedy算法

every once in a while, say with small probability ε, instead select randomly from among all the actions with equal probability, independently of the action-value estimates. We call methods using this near-greedy action selection rule ε-greedy methods.

该算法就是在greedy算法的基础上，有一定的小概率去随机选择那些非当前最佳的action中的一个。

代码如下：

EPSILON = [0.01, 0.1, 0.4, 0.7, 0.9]

def act_epsilon_greedy(type):
    if np.random.rand() < EPSILON[type]:
        return np.random.choice(np.arange(10))

    q_best = np.max(q_estimate)
    return np.random.choice([action for action, q in enumerate(q_estimate) if q == q_best])

结果：

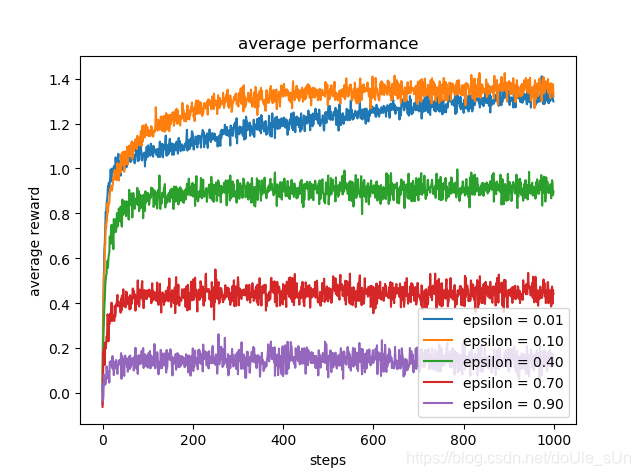
最终Q_t(a)与q*(a)的差距，显然，效果并不是特别好，不过已经好过Greedy算法了：

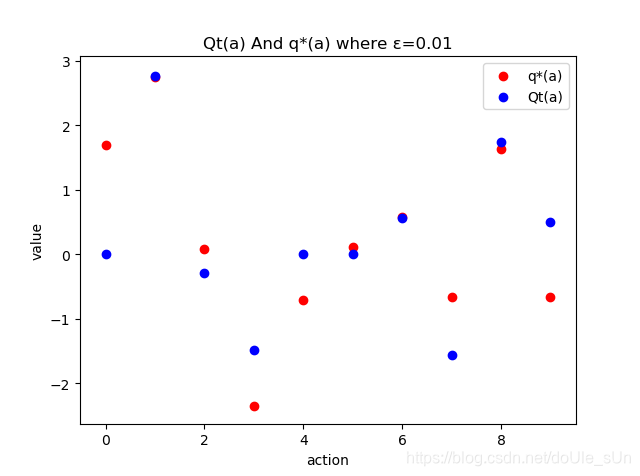
2.4 在这停顿：对算法的改进与补充

2.4.1 Incremental Implementation

根据sample-average method的定义，action value的估计值定义为：

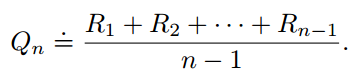
据书上说利用这个公式计算Q_t(a)会消耗很多内存，花费很多时间（我这辣鸡没看出来T_T）。所以拿这个公式开刀，简化成消耗内存时间更少的形式：

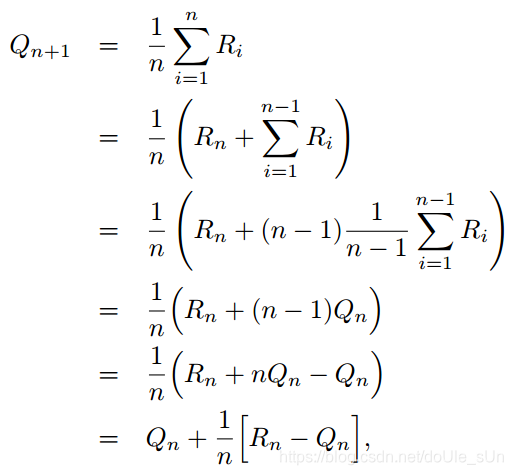
最终简化的结果如最后一行所示。文字描述为：

agent在某一时刻t选中行动a，环境给予奖励R_t，则，新的动作估计值 = 在原估计值的基础上加上目标值（Target）与原估计值的差乘上步长（StepSize学习率）的结果。

实际上我们之前的程序使用的就是这个公式。

依据符号各自的含义，我们可以换一种更普遍的表达形式（重要公式）：

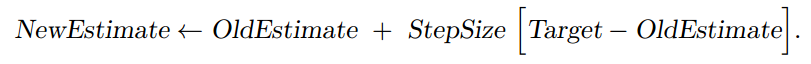
• [Target - OldEstimate]叫做偏差值(error)
• StepSize叫做步长，是一个可以随时刻t改变的参数，记作α_t(a)。关于α的选择我们将在后面叙述

在ε-greedy算法中，步长等于time_step（当前游戏进行次数）的倒数，目标值(Target)为环境给予的第t次奖赏值R_t(a)。

应用Incremental Implementation的ε-greedy算法描述如下：

2.4.2 Nonstationary Problem

• What is nonstationary?

the true values of the actions changed over time.

先前的问题中，我们在开始新一轮游戏前，都先初始化一遍action true value的值，在而后的1000次选择，这10个值都不会改变。这叫做stationary problem。
而如果动作的真实价值q*(a)一直在变化，则变成了nonstationary problem。

• How to address it？

解决方法：使用常数作为StepSize。关于这一部分内容的展开，我们在下一节叙述。

• The importance of nonstationary problem

非平稳问题是强化学习研究内容的重中之重：

problems that are effectively nonstationary are the most common in reinforcement learning.
【注】 在2015版中，使用norm这个词代替most common

• 若之前的问题转变为nonstationary problem，如何解决？

代码将在本文最后一部分Futher More给出。

• nonstationary problem希望见到的情形

the estimates never completely converge but continue to vary in response to the most recently received rewards.

2.4.3 Exponential Recency-weighted Average

先前提到，解决nonstationary problem的方法之一是使用常数作为stepsize，由此，我们可以引出exponential recency-weighted average算法。

公式推导

首先，固定stepsize为常数α，则Q_n+1可以表示为：

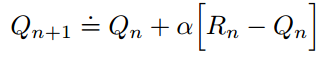
对上式进行恒等变换：

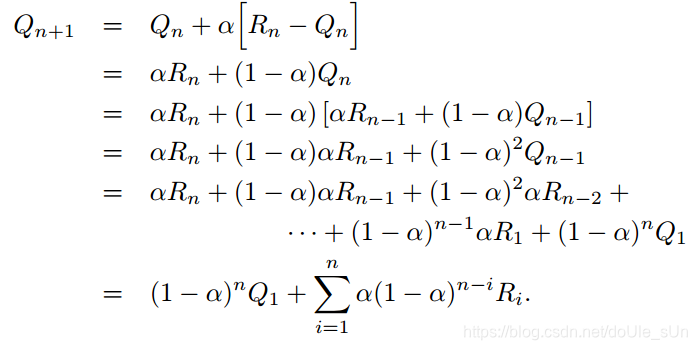
则Q_n+1可以表示为初始估计值Q₁与奖励值R_i的加权求和。

利用等比求和公式可以证明：
$$(1-\alpha {)}^n+\sum _{i=1}^n\alpha (1-\alpha {)}^{{}^{n-i}}=1$$

由此可见，当stepsize固定时，action estimate value可以表示成初始值Q₁和奖励值R_i的加权求和。

公式分析

1. 由于(1-α) <0，所以随着n的增加，Q₁的占比将会以指数形式（exponential）衰减，相对地，R_i的比重将会越来越高。
2. (1-α)越接近于0，则式子的重心越靠近最近的几次R_i（R_n、R_n-1……）

极端情况下我们有：

If 1-α = 0, then all the weight goes on the very last reward, R_n, because of the convention that $$0^0=1$$

StepSize选择的要求：

stochastic approximation theory给出了两个关于stepsize，α_n(a)，的定理：

the conditions required to assure the convergence of α_n(a) with probability 1:
$$\sum _{n=1}^{\infty }{\alpha }_n(a)=\infty and\sum _{n=1}^{\infty }{\alpha }_n^2(a)<\infty .$$

定理的第一个要求保证了收敛不受初值和随机波动的影响，第二个要求保证了最终的stepsize要小到足以保证收敛。

若选择1/n作为stepsize，则满足该定理，保证了最终一定会收敛；
若选择常数α作为stepsize，则第一条要求满足，第二条要求不满足。在这种情形下，正好满足nonstationary problem希望见到的情形，所以我们使用了常数α作为stepsize解决nonstationary problem。

2.4.4 Optimistic Initial Values

所有action estimate依赖于初始值Q₁的算法都会产生一定的偏差（bias）。

For the sample-average methods, the bias disappears once all actions have been selected at least once but for methods with constant α, the bias is permanent, though decreasing over time as given by
$$Q_{n+1}=(1-\alpha {)}^n{Q}_1+\sum _{i=1}^n\alpha (1-\alpha {)}^{{}^{n-i}}{R}_i$$

这种偏差的存在不一定是坏处，也有可能有益处：

• 缺点
  初始值Q₁成为程序需要调的参数之一
• 优点
  可以利用先验知识（prior knowledge）给action estimate value赋初值，帮助选择optimal action。
  还可以鼓励agent积极探索（explore）

对optimistic Initial Value对explore的影响，我们可以设计一个实验观察出来：
在先前的模拟中，我们将q_estimate的每个元素的初始值赋0，现在，我们将初始值全部设置为+5。

Recall that the q*(a) in this problem are selected from a normal distribution with mean 0 and variance 1. An initial estimate of +5 is thus wildly optimistic. But this optimism encourages action-value methods to explore.

给予动作一个远超其真实价值的初始值可以鼓励探索的原因如下：

Whichever actions are initially selected, the reward is less than the starting estimates; the learner switches to other actions, being “disappointed” with the rewards it is receiving. The result is that all
actions are tried several times before the value estimates converge.

代码：

在写。。。