2.1线性分类-part1

分类

目标：给定数据数据 $x$,为其分配一个离散的类标签$C_k$这里$k=1,...,K$
将输入空间分为不同的区域。

如何表示二值类标签

类型标签不再是实数，而是离散集。
两类：$t \in \{0,1\}$
$t=1$表示类$C_1$,$t=0$表示类$C_2$

当类型标签数量大于2时，类如何表示

常用：one-hot 编码，是长度为K的向量，除了位为1外，其他位都为0
例如：给定五类，$\{C_1,C_2,...C_5\}, C_2$可以表示为以下形式

$$t = (0,1,0,0,0)^T$$

广义线性模型

想法：仍然使用上一章回归中用到的线性模型

$$y(\textbf{x}_n,\textbf{w})=\textbf{w}^T\Phi(\textbf{x}_n)$$
但是 $y(\textbf{x}_n,\textbf{w}) \in$ R
当 $y(\textbf{x}_n,\textbf{w}) = 0.71623$时，属于哪一类
使用映射函数 $f$将线性模型映射到离散的类型标签
广义线性模型为
$$y(\textbf{x}_n,\textbf{w}) = f(\textbf{w}^T\Phi(\textbf{x}_n))$$
激活函数: $f(.)$
链接函数: $f^{-1}(.)$

推理和决策

辨别函数

找到一个辨别函数$f(\textbf{x})$直接将输入映射到类标签

生成模型

1、使用贝叶斯理论推断后验分布$p(C_k|x)$,需要考虑先验分布$p(C_k)$和$p(X|C_k)$
也可以对联合分布$p(X,C_k)$建模
2、使用决策论对x分配类
例子：

辨别模型（discriminative model）

辨别模型是确定一个函数，这个函数能直接将输入向量X,映射到K类别中的一类，表示为$C_k$
1、直接计算$p(C_k|X)$
2、使用决策理论（decision theory）为每一个新的X分配一个类型标签

判别函数

两类

先来考虑类型有两类的情况（$K=2$）
建一个关于输入$\textbf{x}$的线性函数

$$y(\textbf{x})=\textbf{w}^T\textbf{x}+w_0$$
当 $y(\textbf{x})>0$时， $\textbf{x}$属于 $C_1$否则属于 $C_2$
决策边界 $y(\textbf{x})=0$是D维度输入空间的（D-1）维超平面
$\textbf{w}$正交于决策平面上的任意向量
证明：令 $\textbf{x}_A$和 $\textbf{x}_B$是决策平面上的两点，则
$$0=y(\textbf{x}_A)-y(\textbf{x}_B)=\textbf{w}^T(\textbf{x}_A-\textbf{x}_B)$$
原点到超平面的距离为

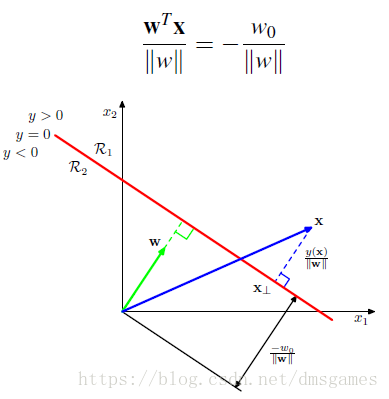
为了让概念更加经凑，给输入空间添加一个额外的维度 $x_0=1$
接着定义 $\tilde{\textbf{w}}=(w_0,\textbf{w})$和 $\tilde{\textbf{x}}=(w_0,\textbf{x})$
$$y(\textbf{x})=\tilde{\textbf{w}}^T\tilde{\textbf{x}}$$
决策平面现在为D+1维输入空间的，D维超平面。

多类

当类型多余2的时候
能否组合K-1个 one-versus-the-rest分类器

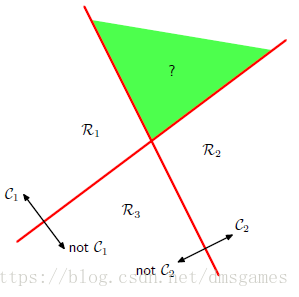
能否组合K（K-1）个one-versus-one个分类器

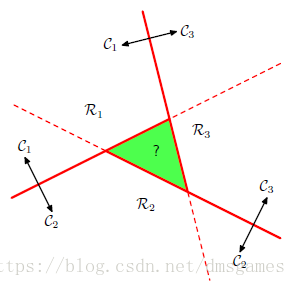
正确的方法：
使用K个线性函数

$$y_k(\textbf{x})=\textbf{w}_k^T+w_{k0}$$
输入 $\textbf{x}$属于 $C_k$当 $y_k(\textbf{x})>y_j(\textbf{x})$对于任何 $j\neq k$
决策平面为
$$y_k(\textbf{x})=y_j(\textbf{x})$$

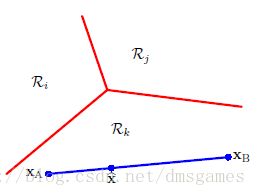
最小二乘

在第一章里面使用最小二乘解决回归问题，分类问题能不能使用这个方法呢，答案是可以的。
给定输入数据$\textbf{x}$属于K类中的一类$C_k$
使用one-hot编码
判别函数为

$$y(\textbf{x})=\tilde{\textbf{W}}^T\tilde{\textbf{x}}$$
对于一个新输入的 $\textbf{x}$，它的类型由值最大的 $y(\textbf{x})$决定。

如何求$\tilde{\textbf{W}}$

给定训练集{$\textbf{x}_n,\textbf{t}$}其中$\textbf{t}$是one-hot编码。
定义矩阵$\textbf{T}$其中第n行对应$t_n^T$
误差和可以写为

$$E_D(\tilde{\textbf{W}})=\frac{1}{2}tr\{(\tilde{\textbf{X}}\tilde{\textbf{W}}-\textbf{T})^T(\tilde{\textbf{X}}\tilde{\textbf{W}}-\textbf{T})\}$$
当
$$\tilde{\textbf{W}}=(\tilde{\textbf{X}}^T\tilde{\textbf{X}})^{-1}\tilde{\textbf{X}}^TT$$
时候误差取到最小值

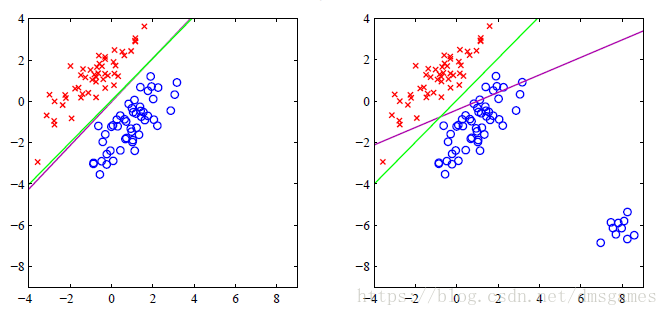
上图中绿线是逻辑回归的决策平面，紫线是最小二乘线性回归的决策平面，可以看到二小二乘的决策平面容易受到离群点扰动。
为什么会这样呢？
这是因为最小二乘训练的时候每一个训练数据对决策平面都具有相同的影响，而逻辑回归通过sigmoid激活函数降低了离群点对决策平面的影响。