邓俊辉 数据结构二叉搜索树

二叉搜索树（概述 循关键码访问）

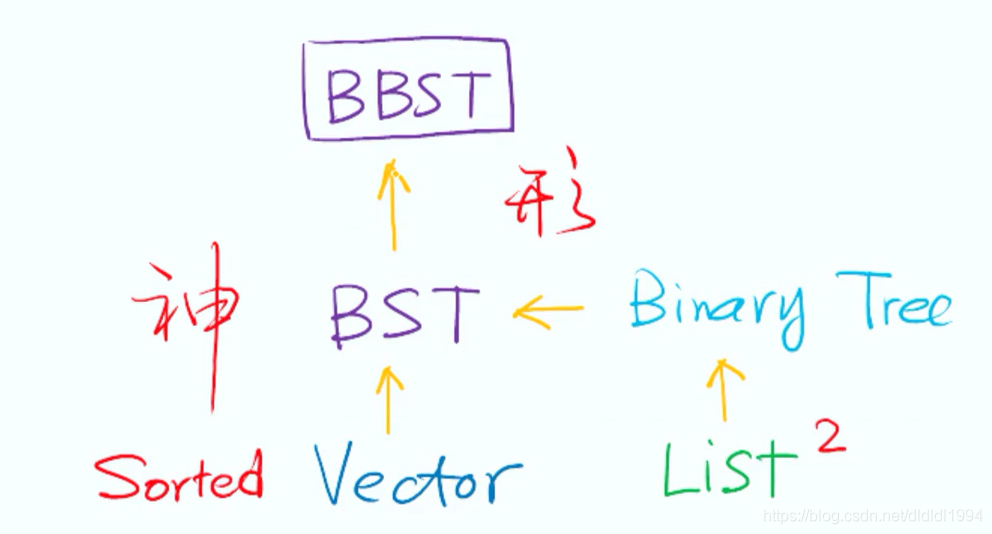
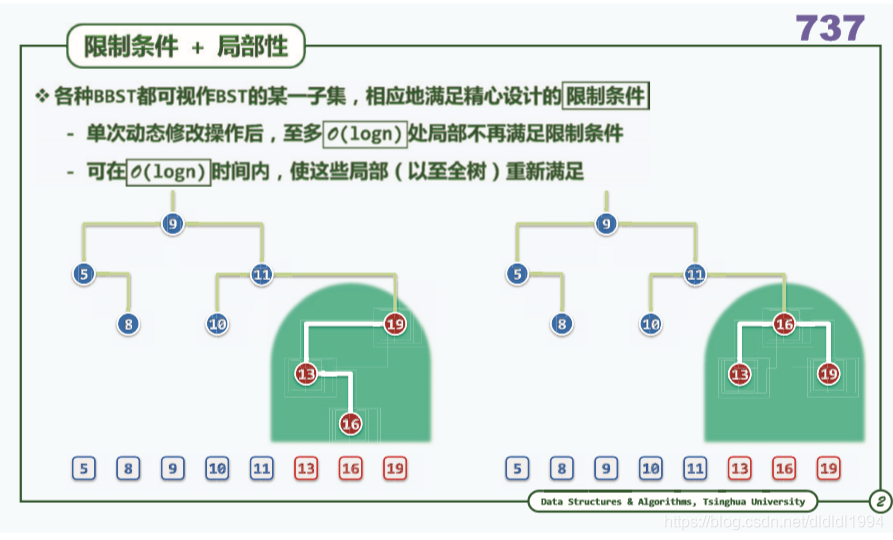
BST（二叉搜索树）形式上继承了二叉树，同时又借鉴了有序向量的特性，这特别体现在BST的子集BBST（平衡二叉搜索树）

问题：为什么说二叉树是列表的列表呢（by xiaoxiaolin）
答：这句话在《数据结构（上）》第五章 05A-1

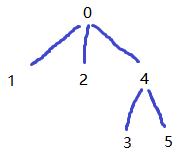
描述一棵树的时候，只需要把每个节点的孩子描述清楚，这棵树就唯一确定了。因此树可以看作节点的列表，每个节点是children的列表。

例如tree = [[1,2,4], [], [], [], [3,5], []]，表示这棵树有6个节点，0号节点有三个子节点，分别是1、2、4号节点……

（by yuantailing 老师）
你可以先考虑“一维的树”这个概念。“一维的树”就是说父亲只有一个儿子，（一叉树） 然后你把“一叉树”画出来，会发现“一叉树”就是列表（by LogM）

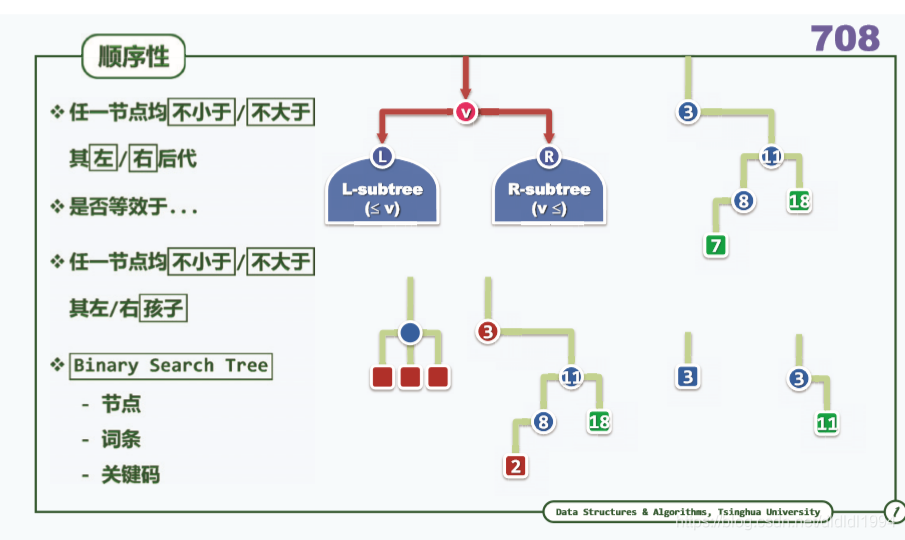
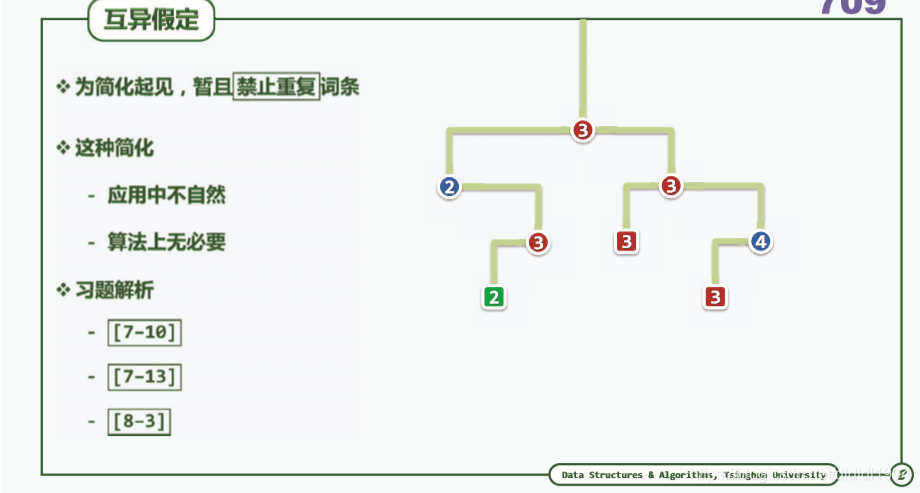
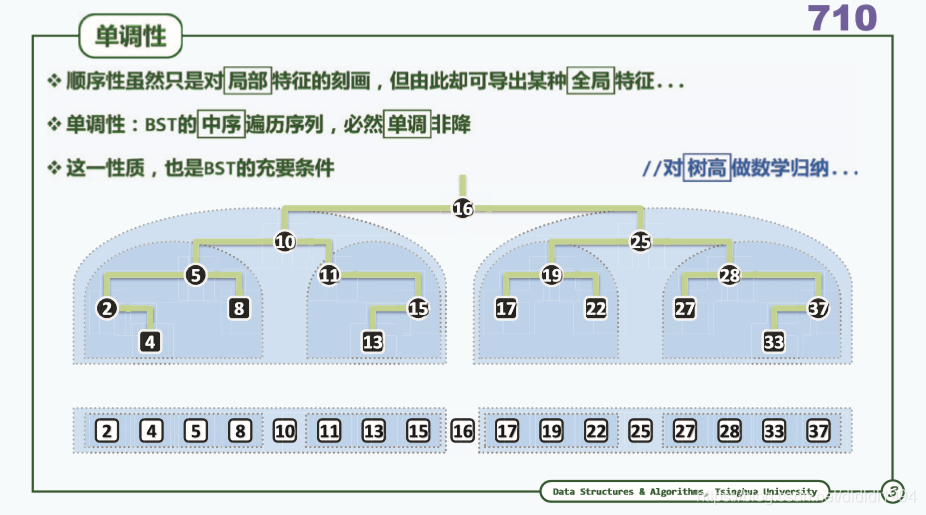
二叉搜索树（概述 中序）

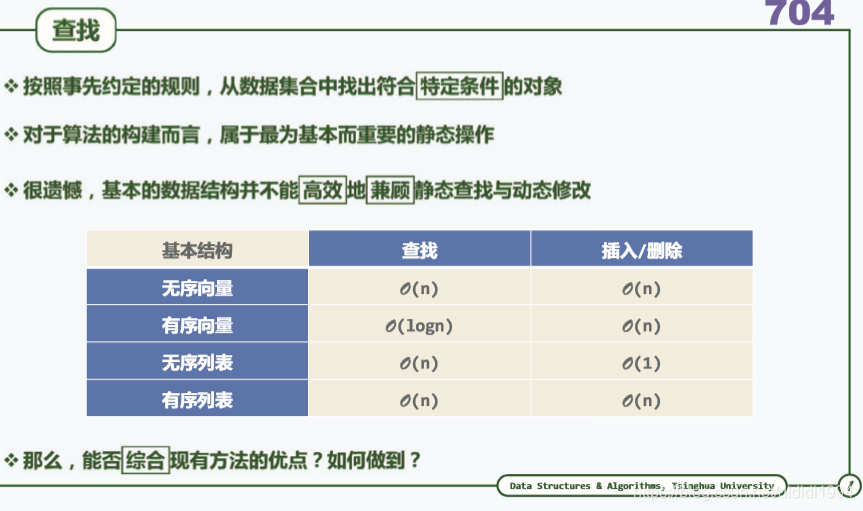
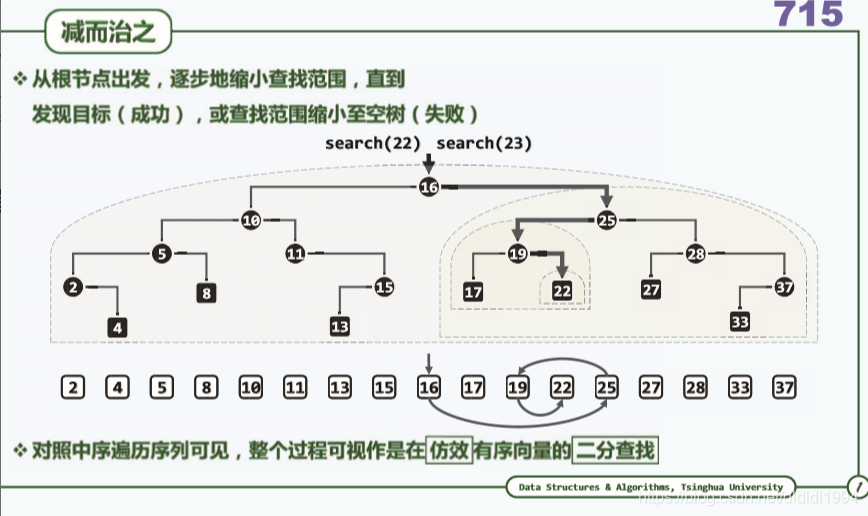
二叉搜索树（算法及实现 查找）

指针与引用之易混点辨析
最近学习搜索树时发现一些可能大家需要注意的地方，特别是“引用与指针”，现做一总结：

所谓引用，指给某个变量换一个名字，即新名字和原名字都代表内存的同一区域，调用者可通过它们的任意一个来改变其对应内存中的数据

所谓指针，指一个变量的内存地址，通过地址可以访问和修改对应的变量。

所谓指针变量，它是一个变量，也在内存中占据一定空间，但保存了某个变量的指针。

观察BST相关操作，我们会发现，search操作的返回值是一个引用，是一个指针变量的引用，这个指针变量，或者说这个指针变量保存的地址指向了找到的节点。那么我们为什么需要引用？因为我们需要得到找到节点的位置？不是，因为我们需要修改找到节点？也不是。上述2个功能，没有引用，也可以完成，因为有原指针变量保存的地址，在另一个函数中用临时变量保留这个指针变量，也即保留了地址，立即就能通过这个地址访问和修改地址对应的节点。那么引用到底是为了什么？教材或视频中都说为了后续操作，但未说具体什么操作，我想有人可能马上会说，当然是插入和删除，但是确切地说，不是删除，而是插入。

插入操作势必会给找到节点位置分配一个新节点，而这个分配节点的操作就会改变找到节点的位置，换句话说，插入操作需要修改的是地址，而不是找到的节点！如果你想修改某个普通变量，那么你需要引用这个变量，如果你想修改某个地址，那么你需要引用这个地址所被保存的变量，也就是指针变量，这就是引用指针（变量）的真正目的。至于删除操作为什么也使用引用，我想大概是为了统一操作接口的规范，但统一归统一，概念可不能混淆。

总的来说，引用指针（变量）的目的就是为了改变指针，而这个操作一般体现在分配新节点时，一旦分配了新节点，当前引用到的指针被改变，之后只需通过这个指针修改其指向的对象即可，而指针本身一般不再去改变。（by 不羁的逆袭）

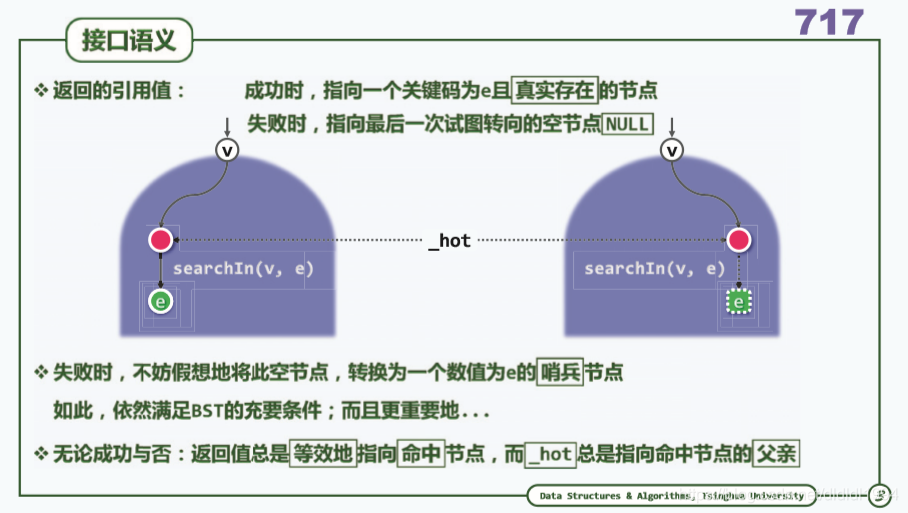
二叉搜索树（算法及实现 插入）

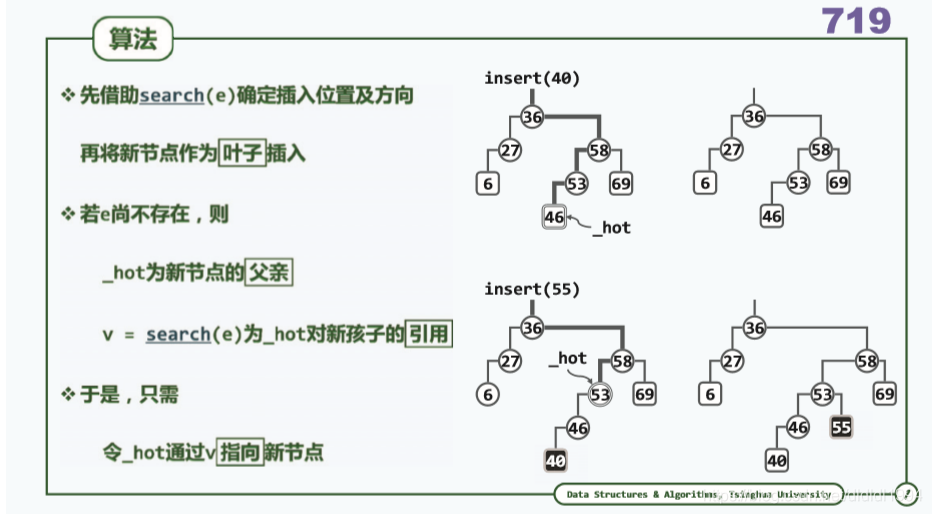
问题：
我有个小疑问：这里返回的hot为待插入节点e的父节点，，但是e可以作为左孩子或者右孩子接入，此处并没有明确给出是哪一种。
所以，BinNode()这个构造函数针对BST类做了重载吗？
比如，取出e的data和hot的data进行比较，选择到底是把e作为hot的左孩子还是右孩子。
一般来说，这之类的辅助功能到底是放在重构函数里面实现，还是放在这里的insert()函数里面实现？有没有可参考的标准呢？（by HelloZH ）
答：第一个问题：没有

第二个问题：x是hot的哪个孩子就把e作为hot的哪个孩子

new BinNode(e, _hot) 只是把新建节点的 parent 设为 _hot ，没有把 _hot->?Child 设为新建的节点。

x 是 _hot->?Child 的左值引用，是在 x = … 这个等号把 _hot->?Child 设为新建的节点的。（by yuantailing 老师）
我明白了，因为search()返回的是&类型，所以修改x等价于修改了_hot->?child，所以
x=NewNode等价于 _hot->?child = new node
而右边new BinNode(e,_hot)实现的是：NewNode->parent = _hot
谢谢老师了！（by HelloZH ）

二叉搜索树（算法及实现 删除）

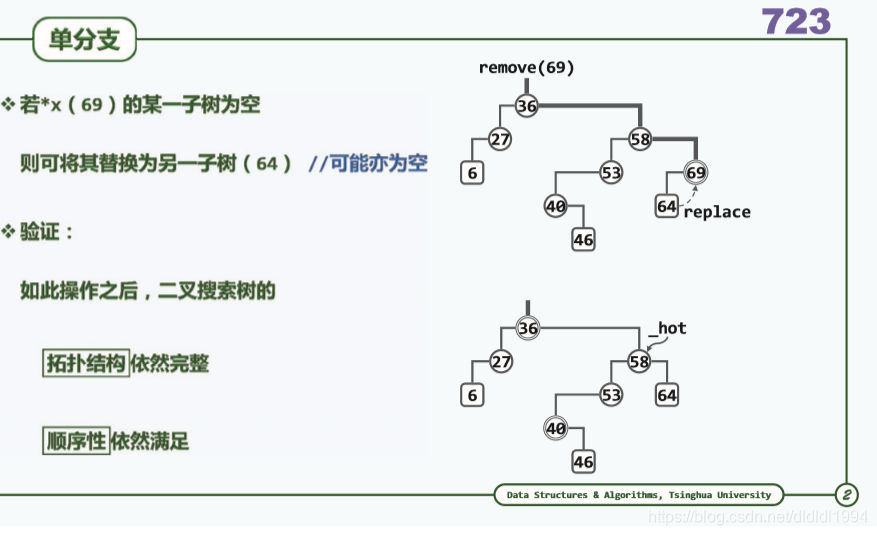
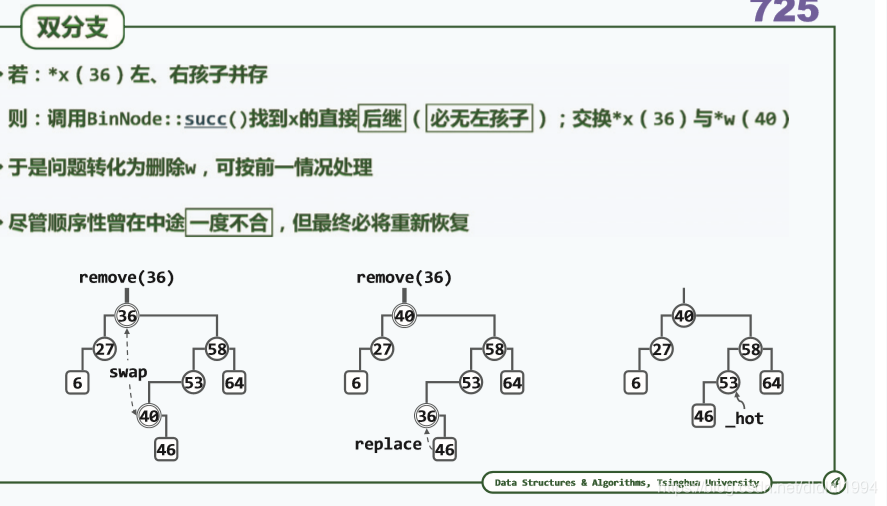
x的直接后继：先转向右子树，然后一直沿左子树下行

对removeAt()算法的一些想法
首先关于语句“((u==x)?u->rc:u->lc)=succ=w->rc”，我刚开始没看懂，后来仔细分析了才理解。我发现无论是教材或视频，邓公都一笔带过了，而讨论区又有一些对此有疑问的帖子，看来邓公的“显然”的确对一些初学者来说是不“显然”的啊，希望在教材以后的版本中能多加几句注释。其次我说下我对此句的理解，以便后来的同学作参考：

此处有两种情况，第1种情况，x也是w的父亲，也就是说u等于x，那么按照中序遍历，w若要作为x的直接后继必然是x的右孩子，第2种情况，u不是x，即x不是w的父亲，那么根据中序遍历，w必然是u的左孩子。然而无论何种情况， w不可能有左孩子，所以u的左或右孩子只能被w的右孩子（可能不存在）替代，同时接替者也被w的右孩子替代。需要注意的是，此时u的孩子指针改变，w不再是u的孩子，但是w的父指针仍然指向u，所以hot就可以通过w来记录被删节点的父亲，若接替者存在，就将其与hot连接，最后因为w仍然指向被删除节点的位置，释放w，删除完成。(by 不羁的逆袭 )
u不等于x：

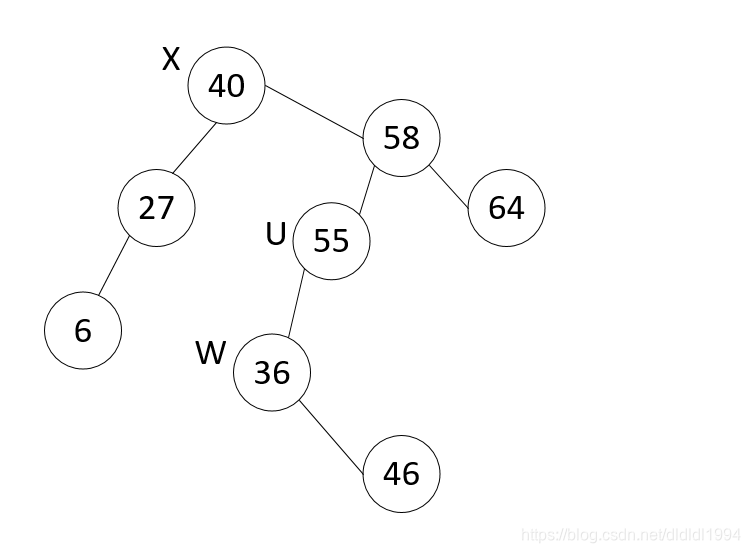
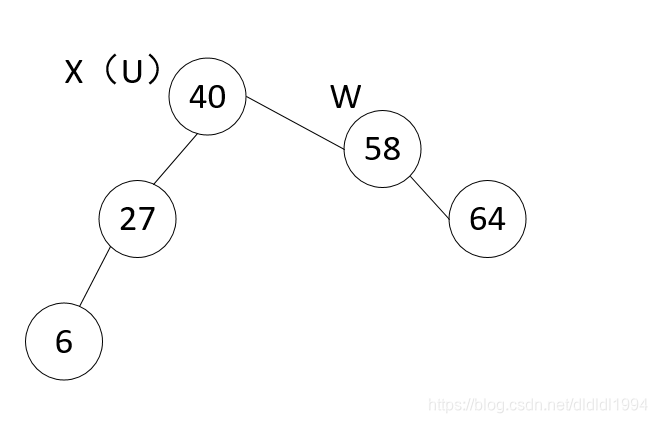
u==x：被删除节点的右子树没有左孩子的情况

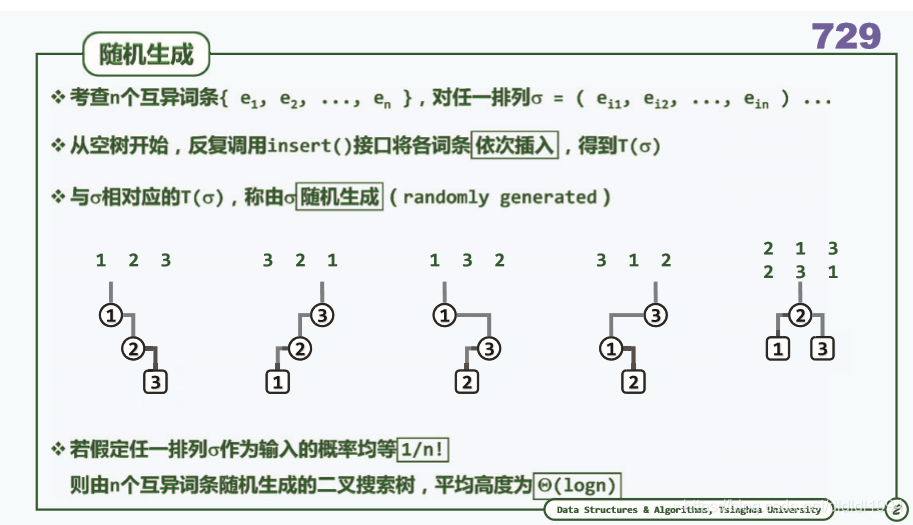
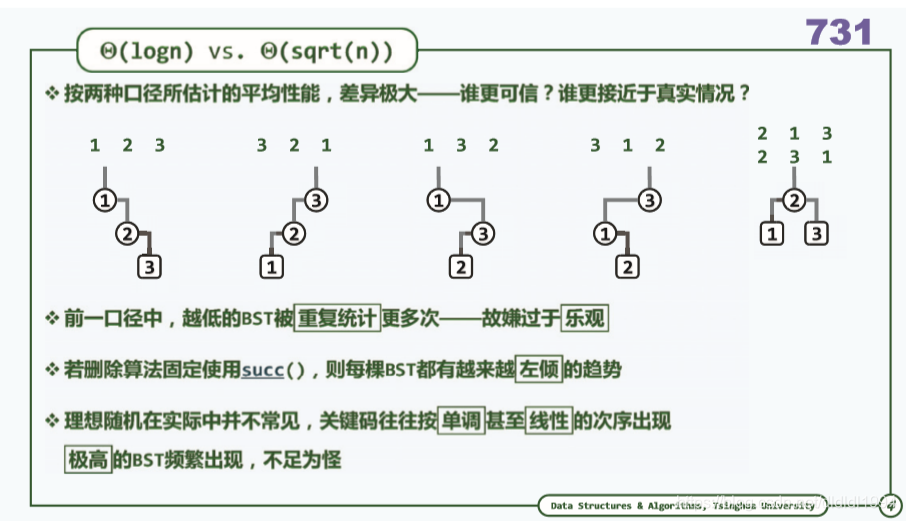
二叉搜索树（平衡 期望树高）

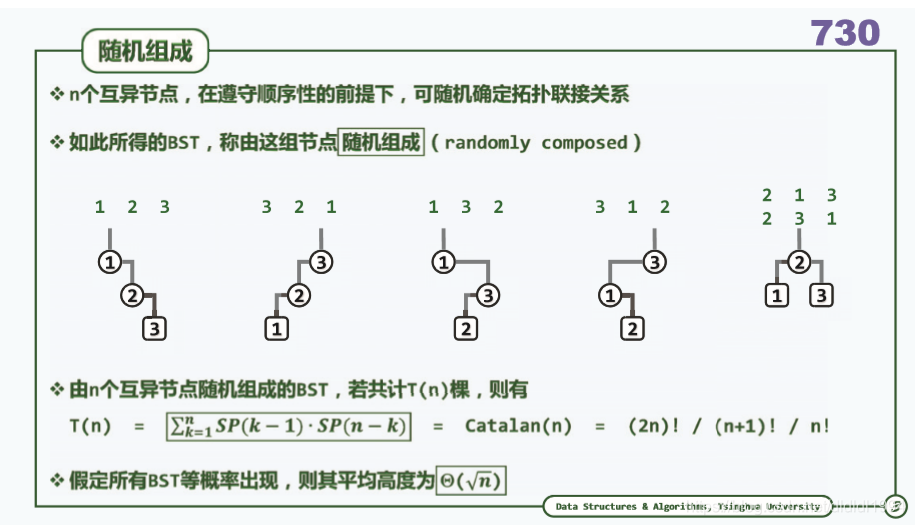
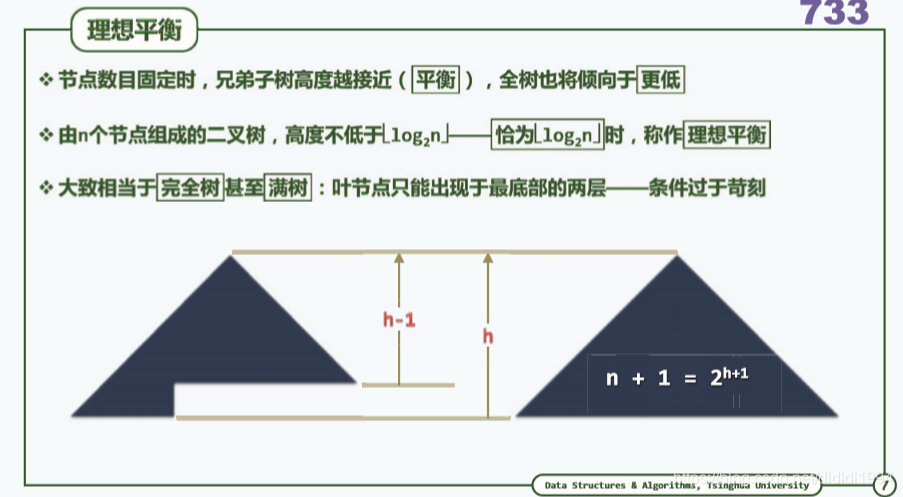
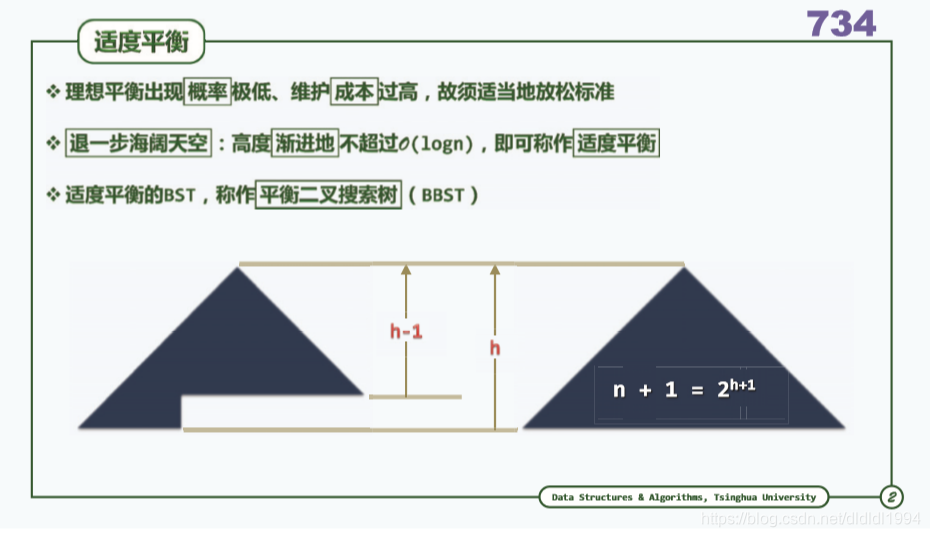
二叉搜索树（平衡 理想与适度）

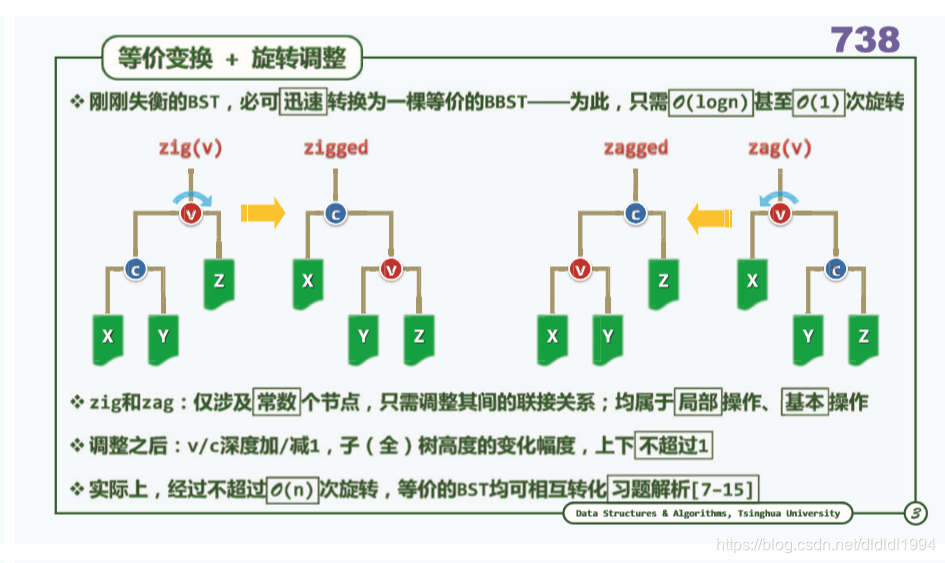
二叉搜索树（平衡 等价变换）

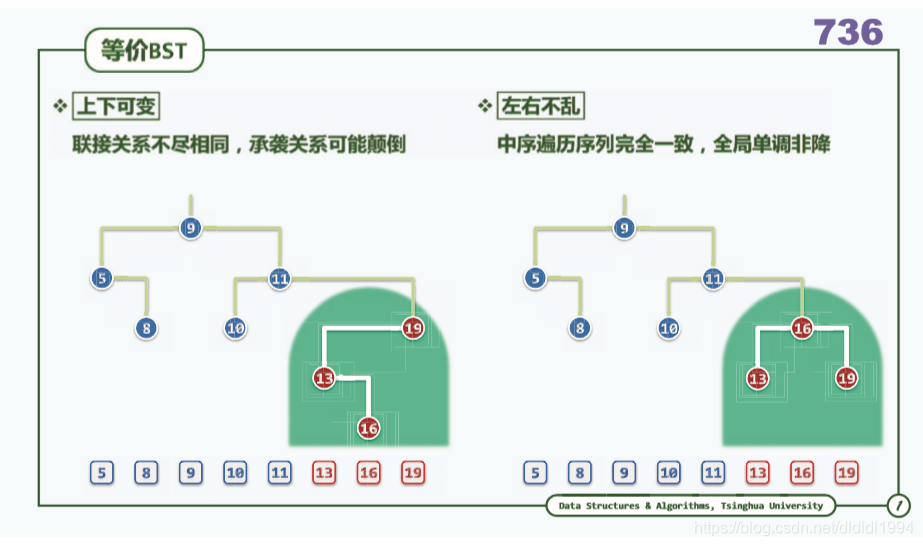
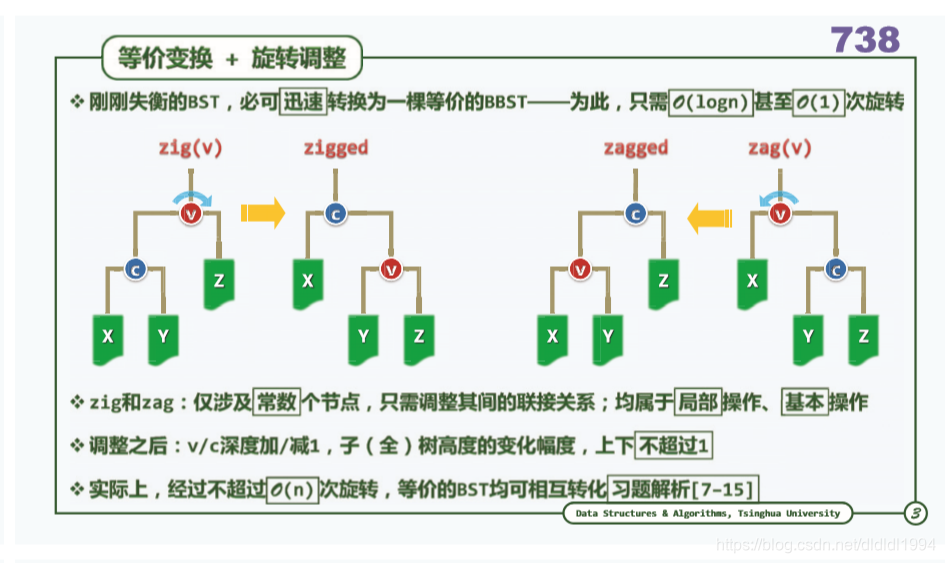
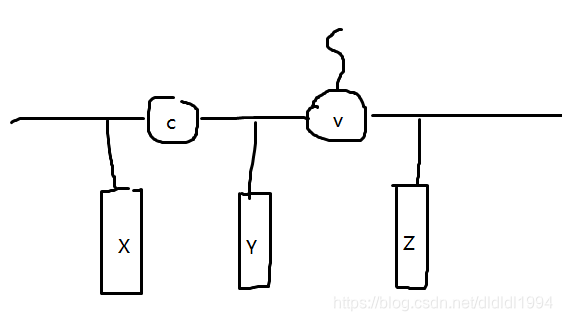
还可以想象成一串珠子下面挂着风铃。提着 c 还是提着 v 的区别。

zig 是从提着 v 变成提着 c。

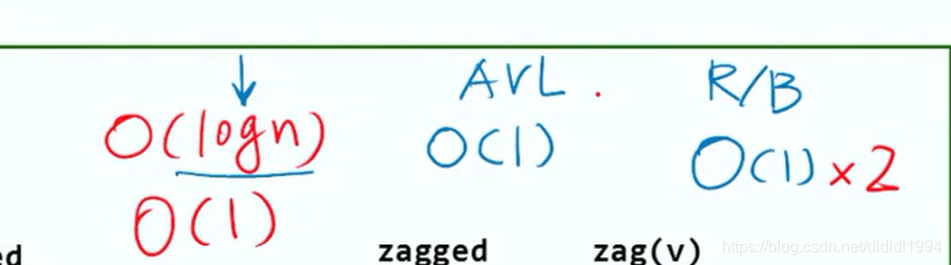
AVL：时间O(1) 操作次数 O(log n)
红黑树：时间O(1) 操作次数 O(1)

二叉搜索树（AVL树 适度平衡）

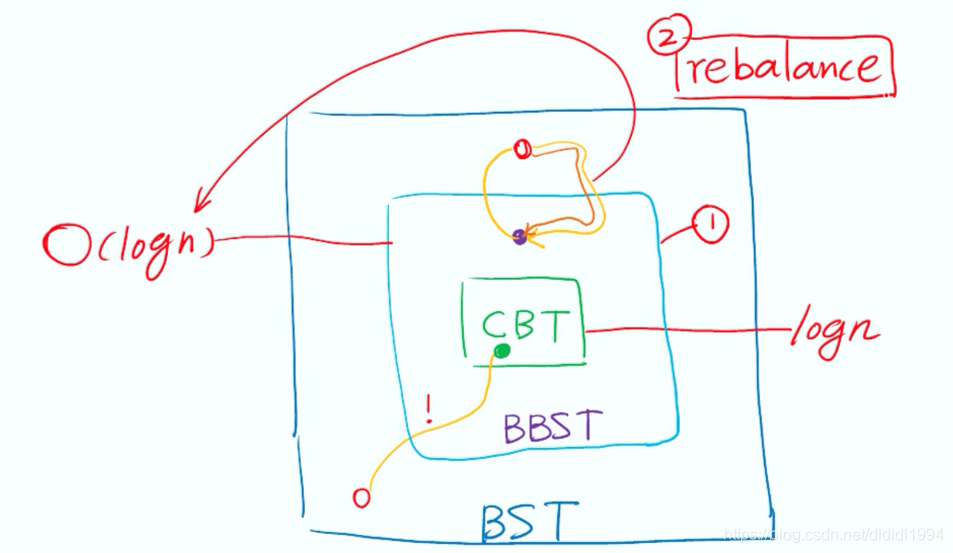
BST ：二叉查找树，但是它的高度不能令人满意，CBT （完全二叉树）的高度最低，为logn，但是从BST转换到CBT的代价很高，所以我们要放宽标准，只需渐进意义的logn即可，即O（logn），此类树即为BBST（平衡二叉搜索树），该类树即使不满足平衡标准，但是可以用极小的代价，通过等价变换，不超过O（logn）拉回到BBST，BBST： 1： 如何判断失衡 2： 如何进行再平衡
AVL就是一种BBST

二叉搜索树（AVL树 适度平衡）

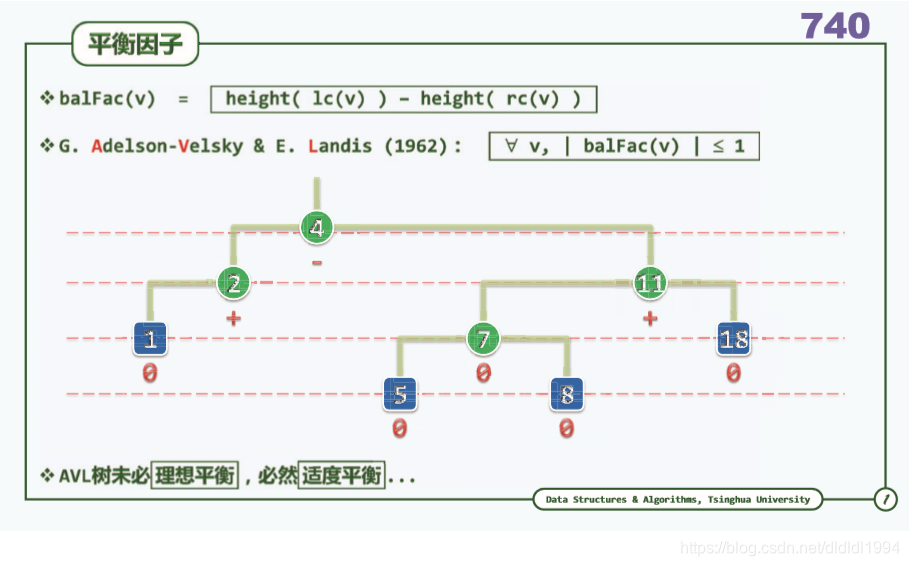
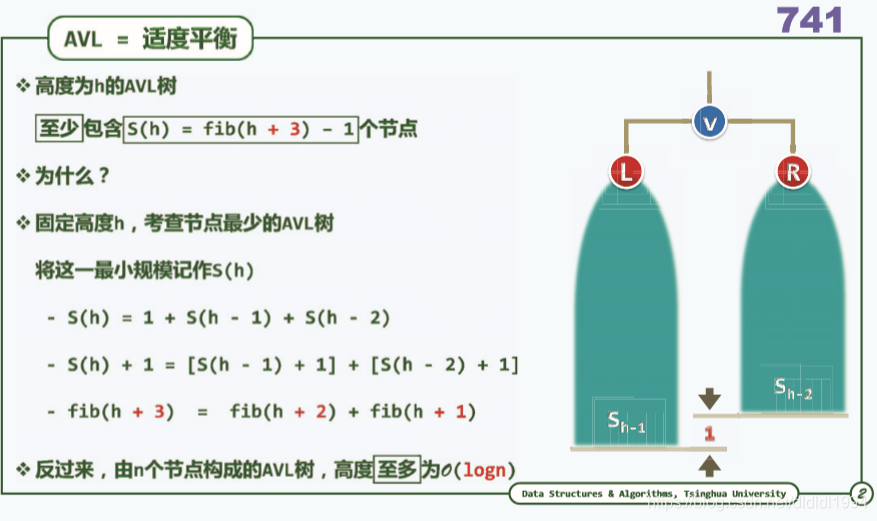
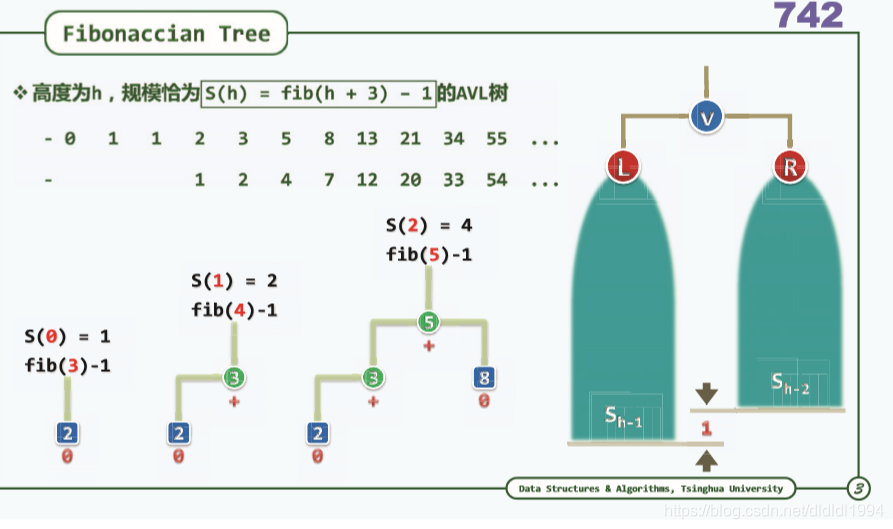
二叉搜索树（AVL树 重平衡）

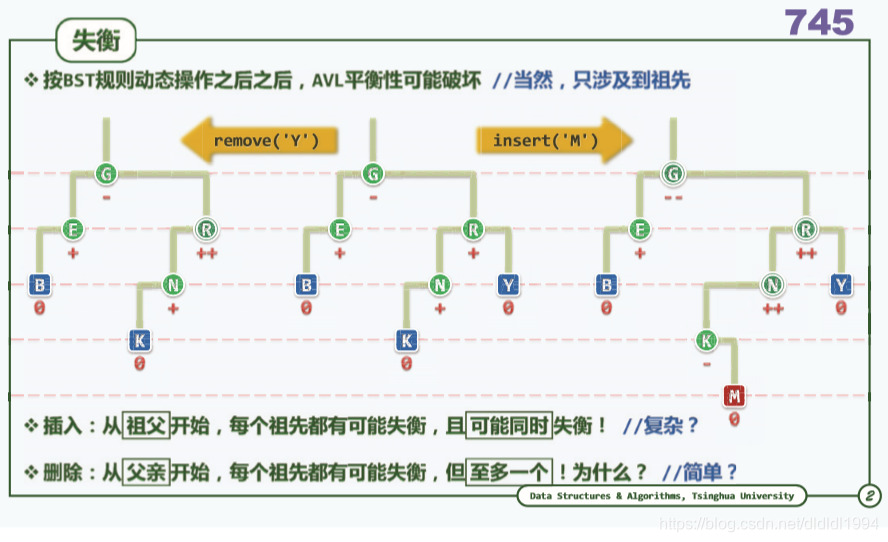
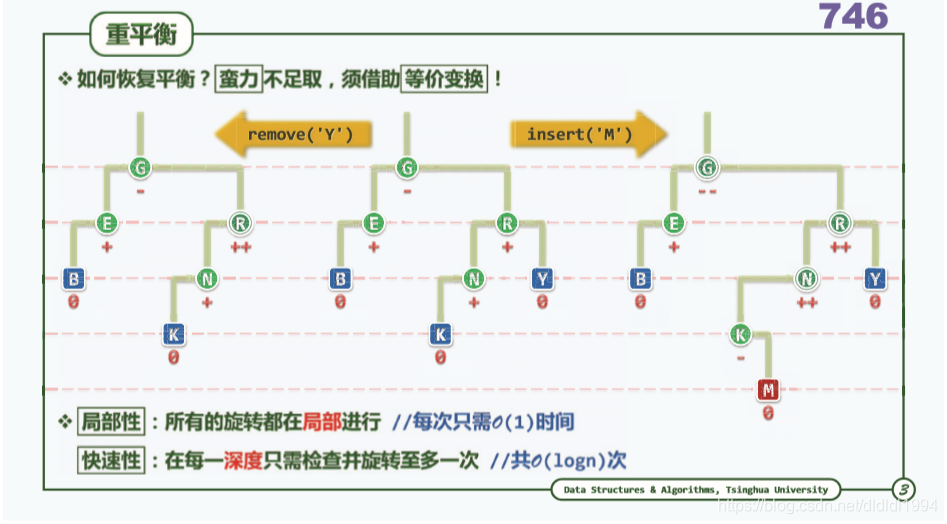
二叉搜索树（AVL树 插入）

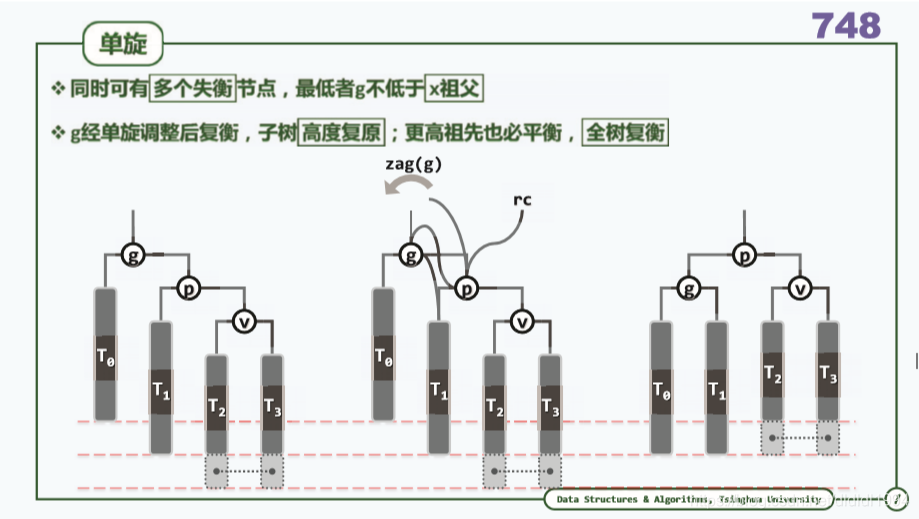
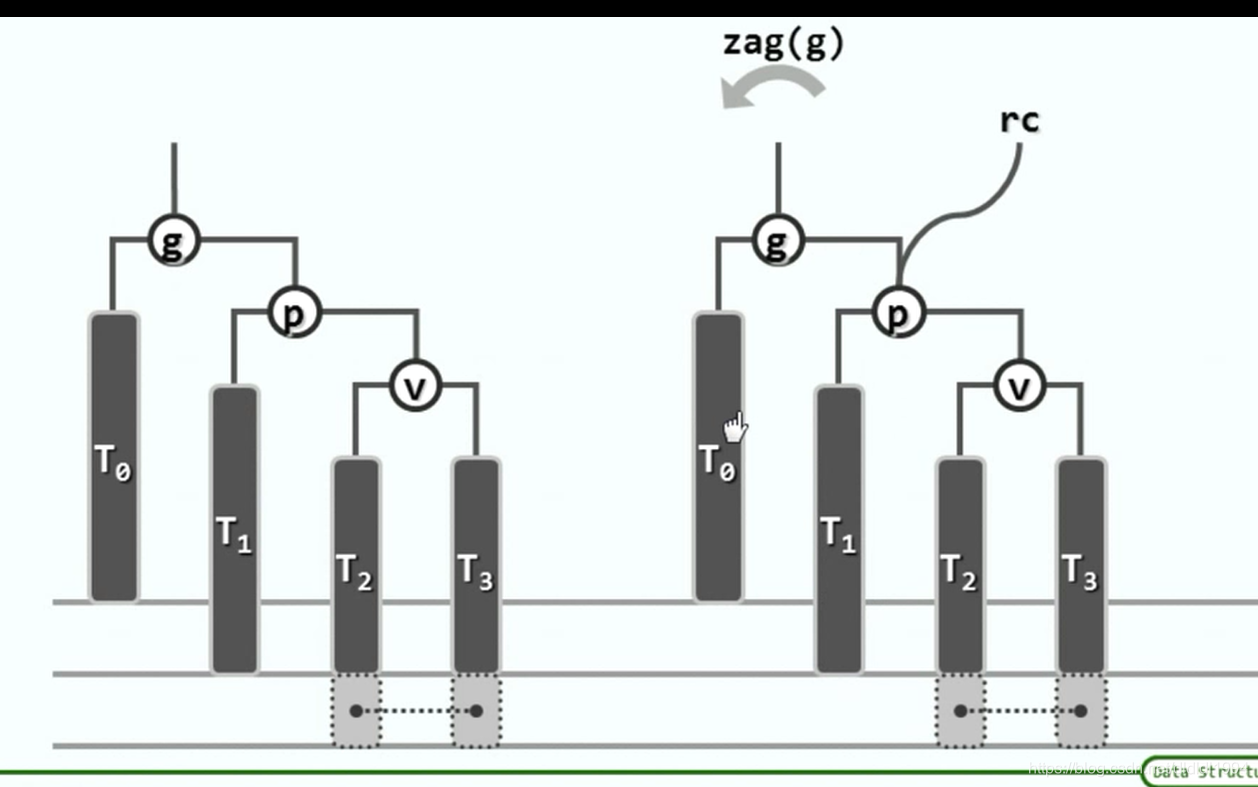
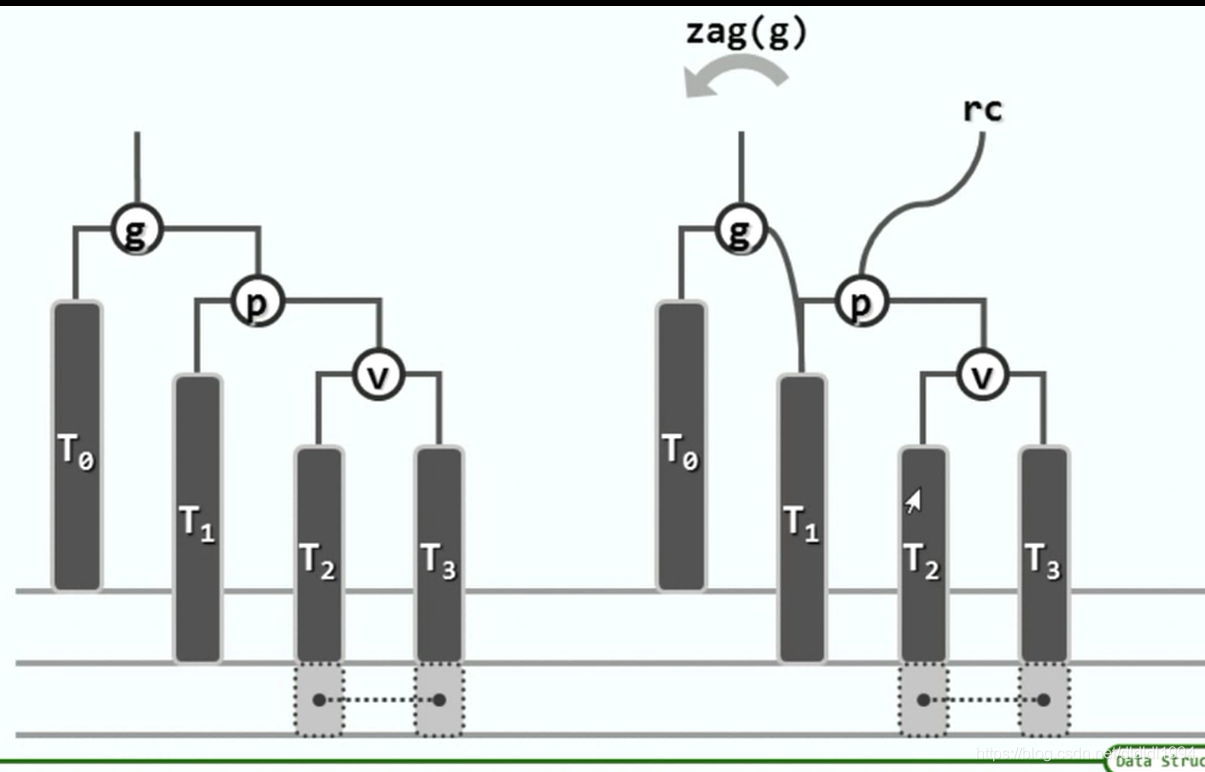
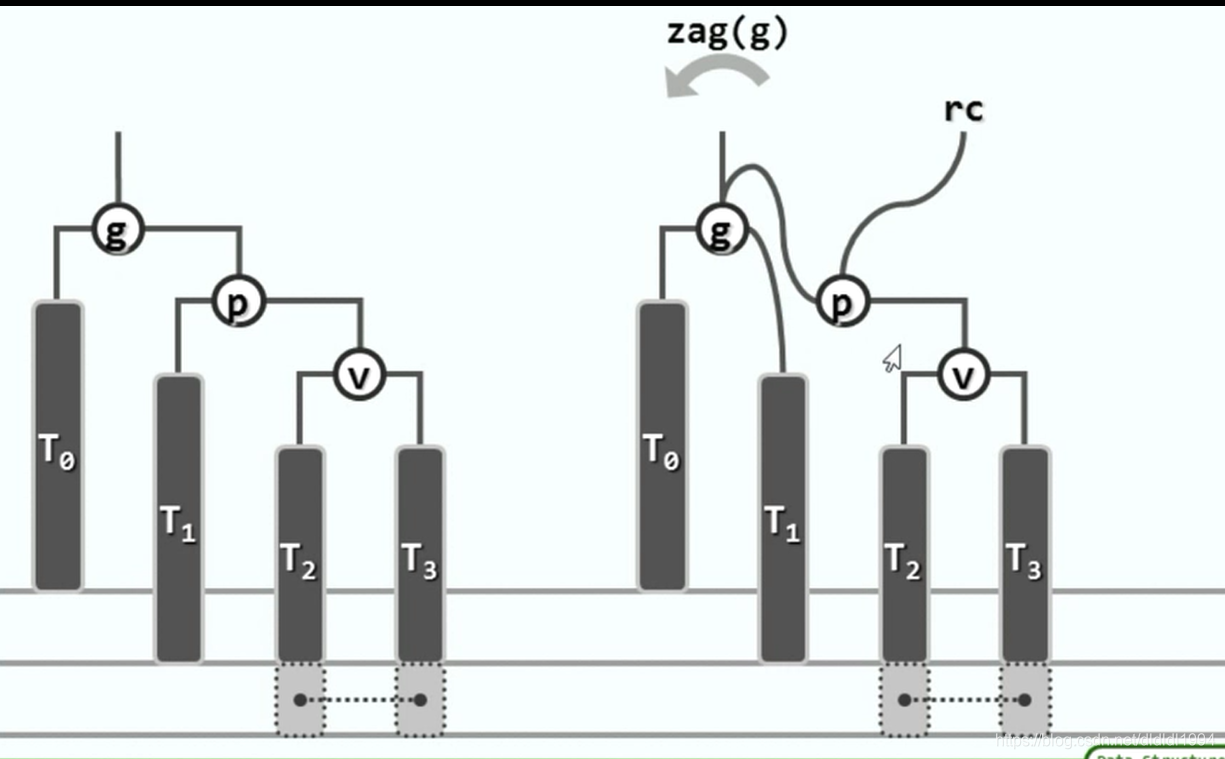
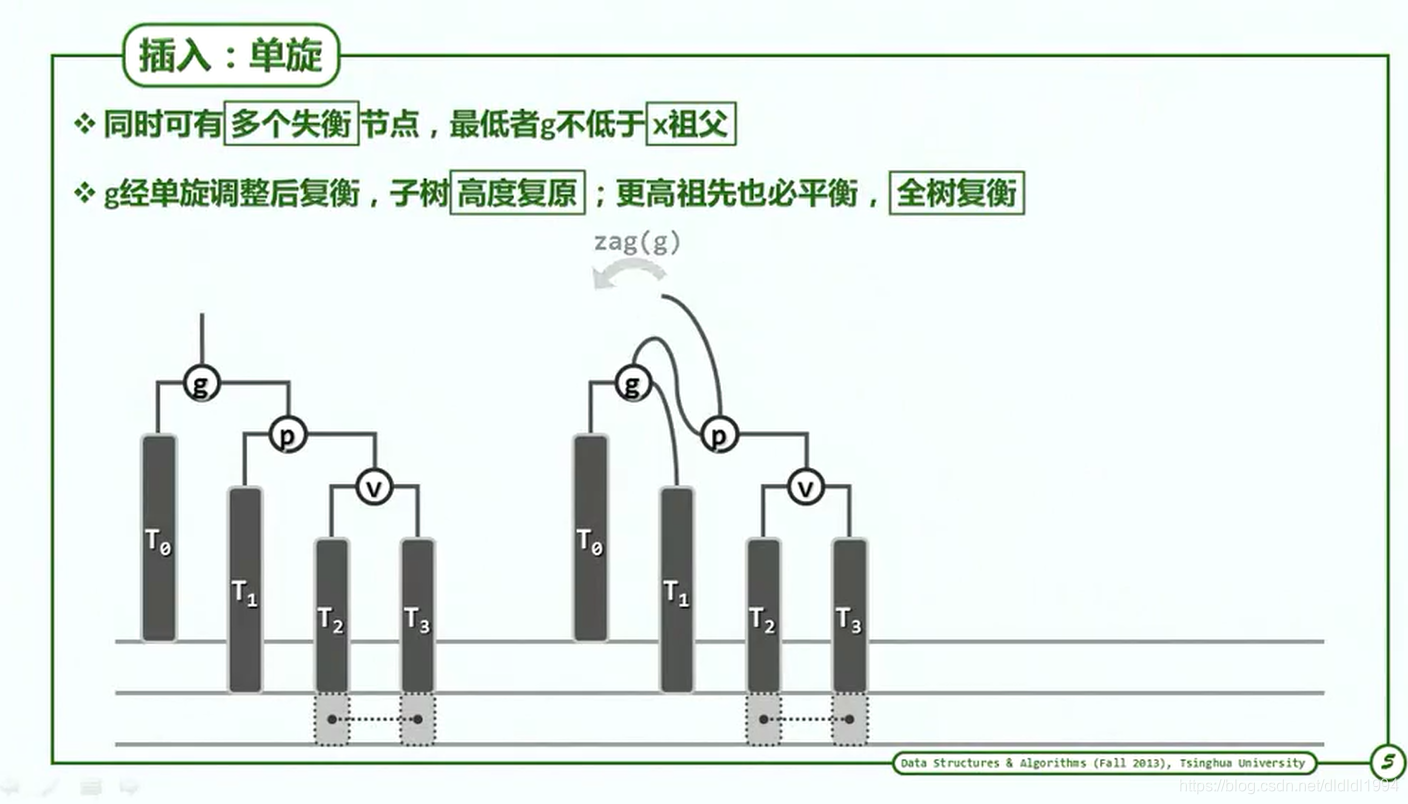
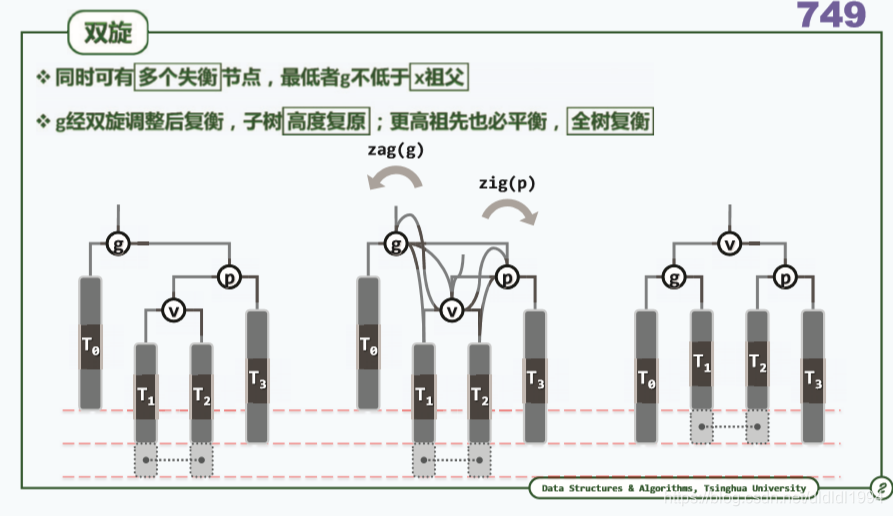
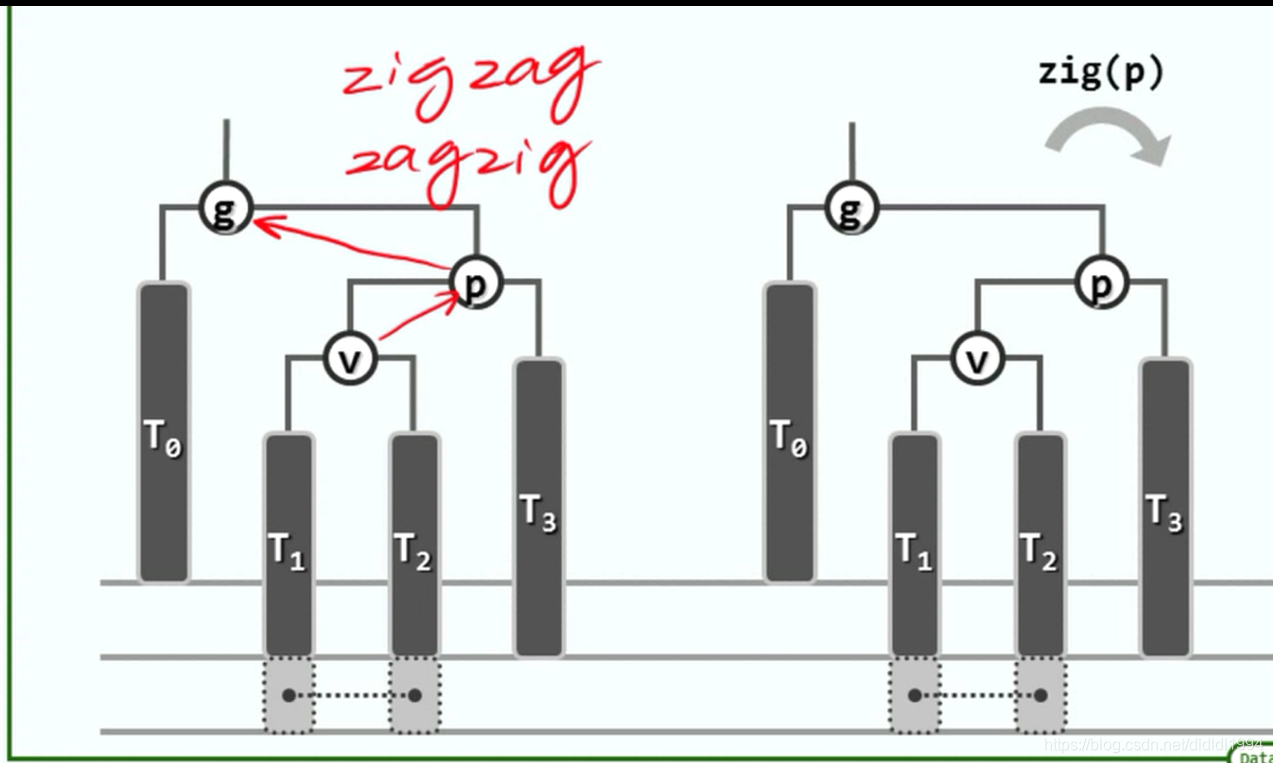
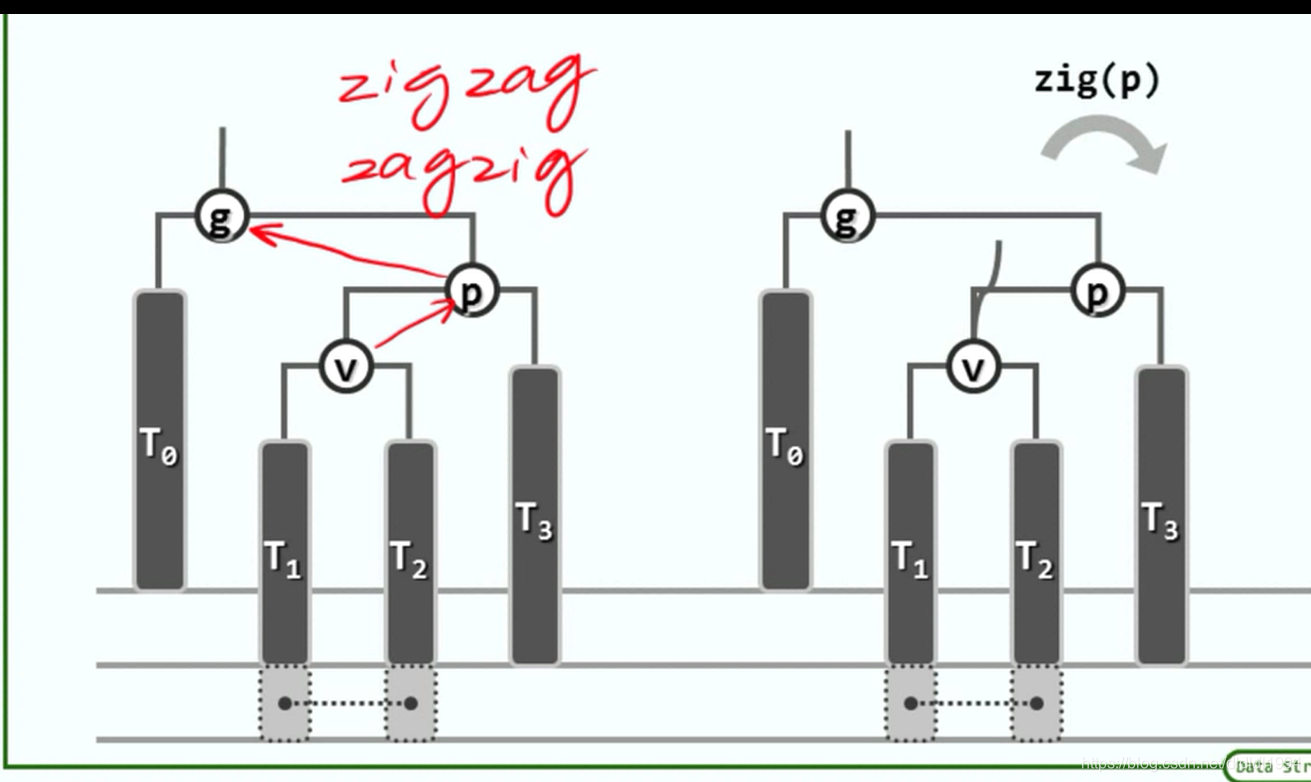
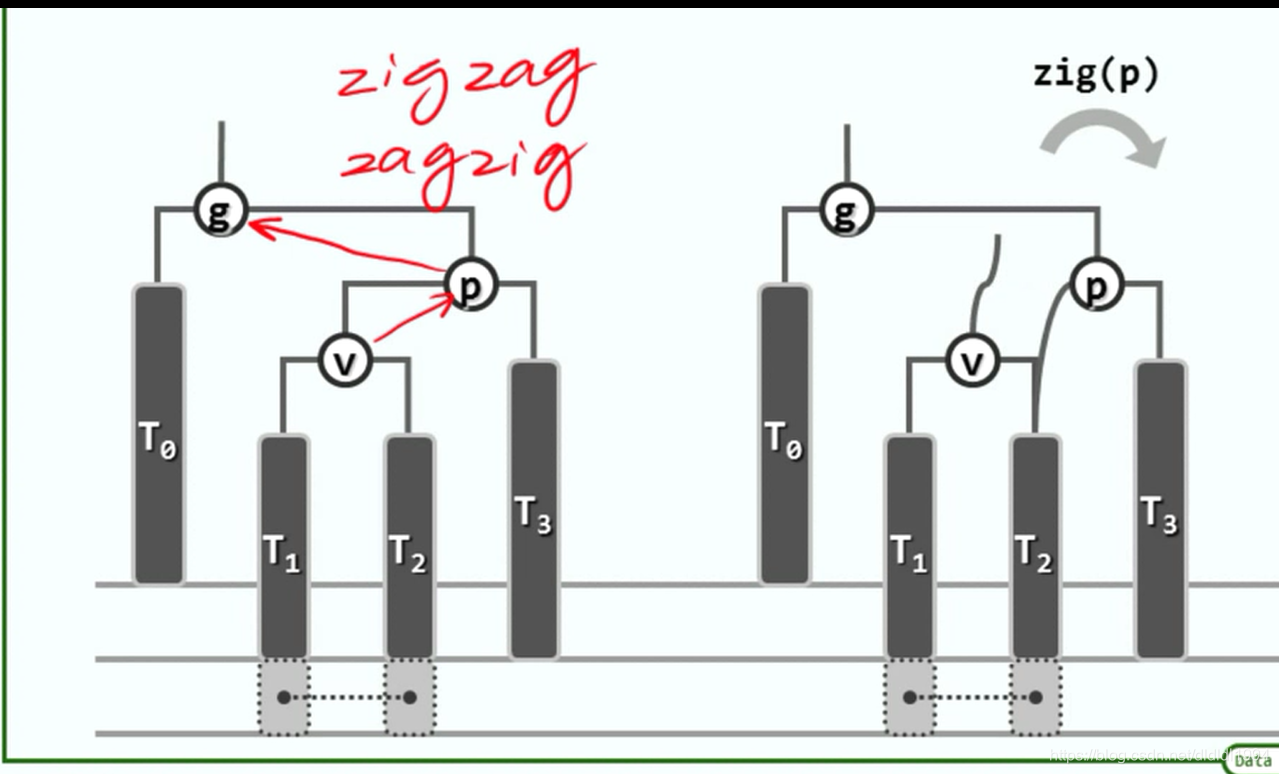
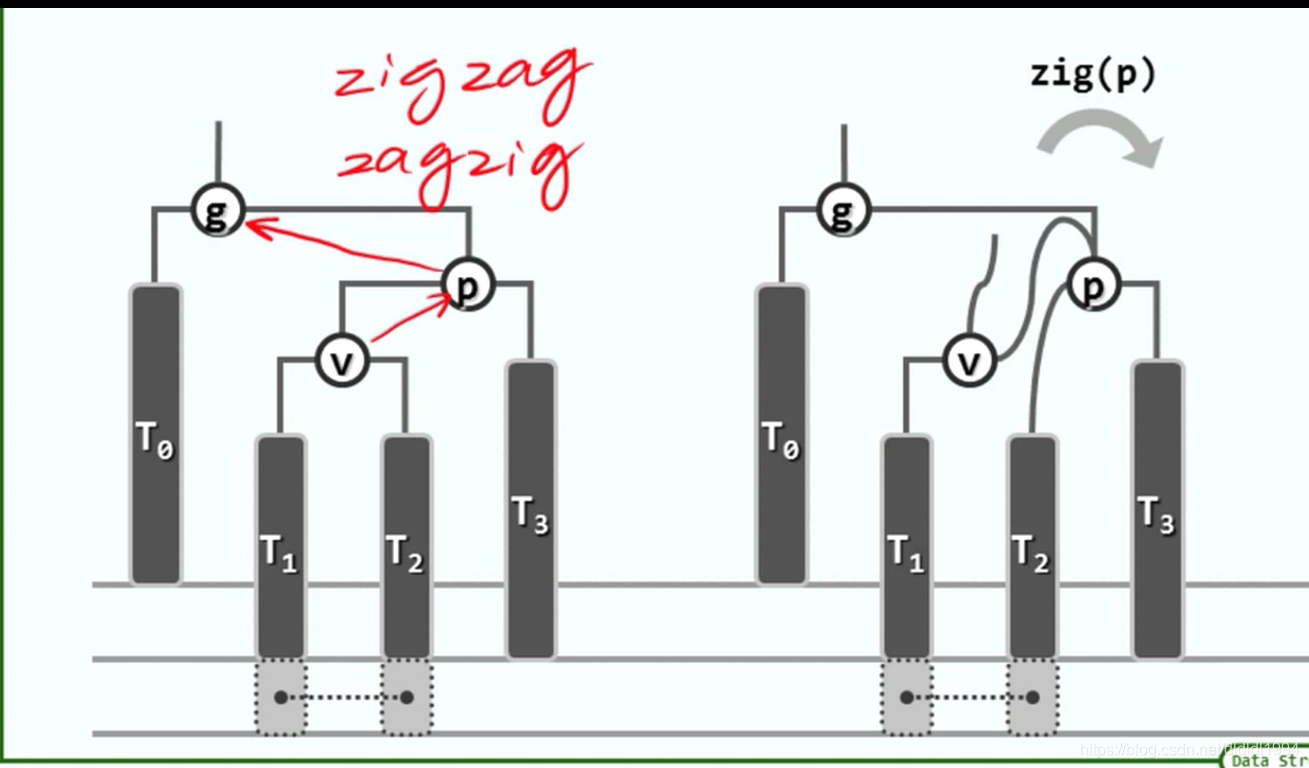
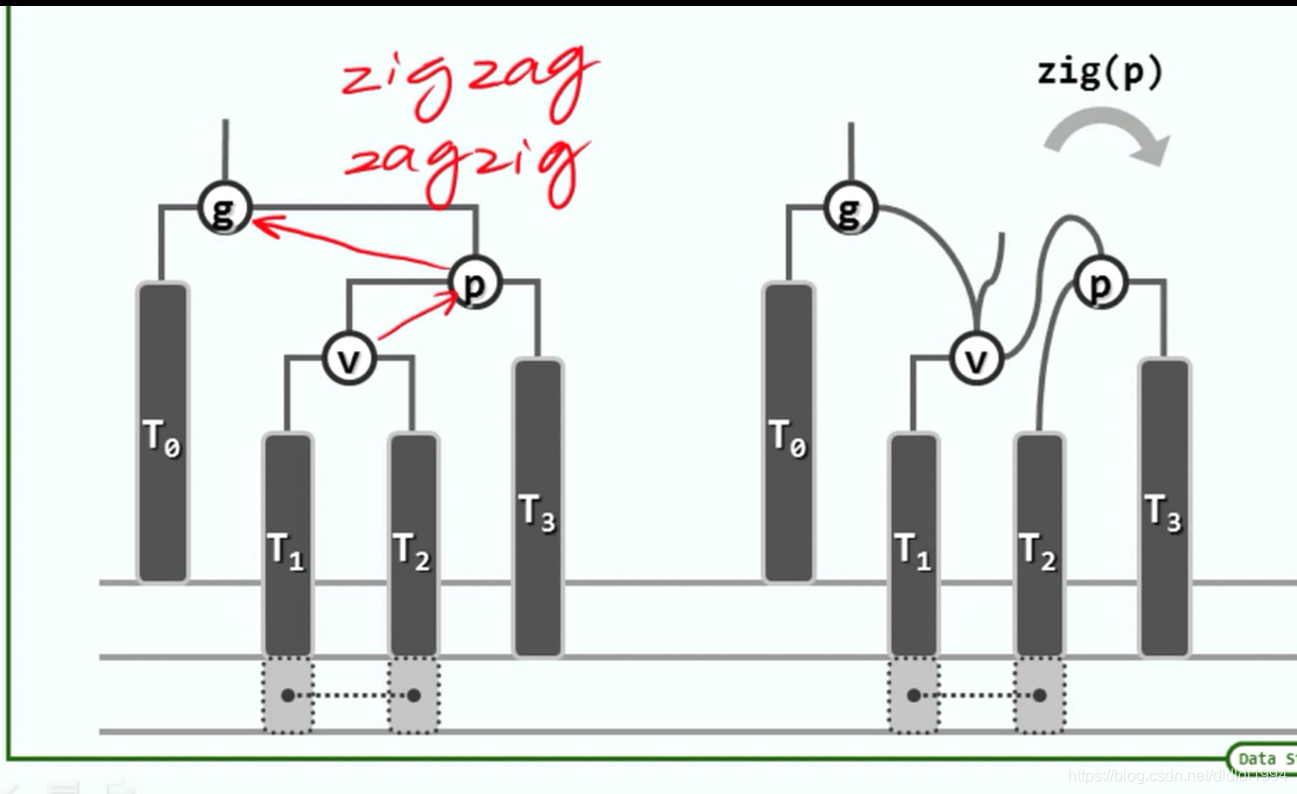
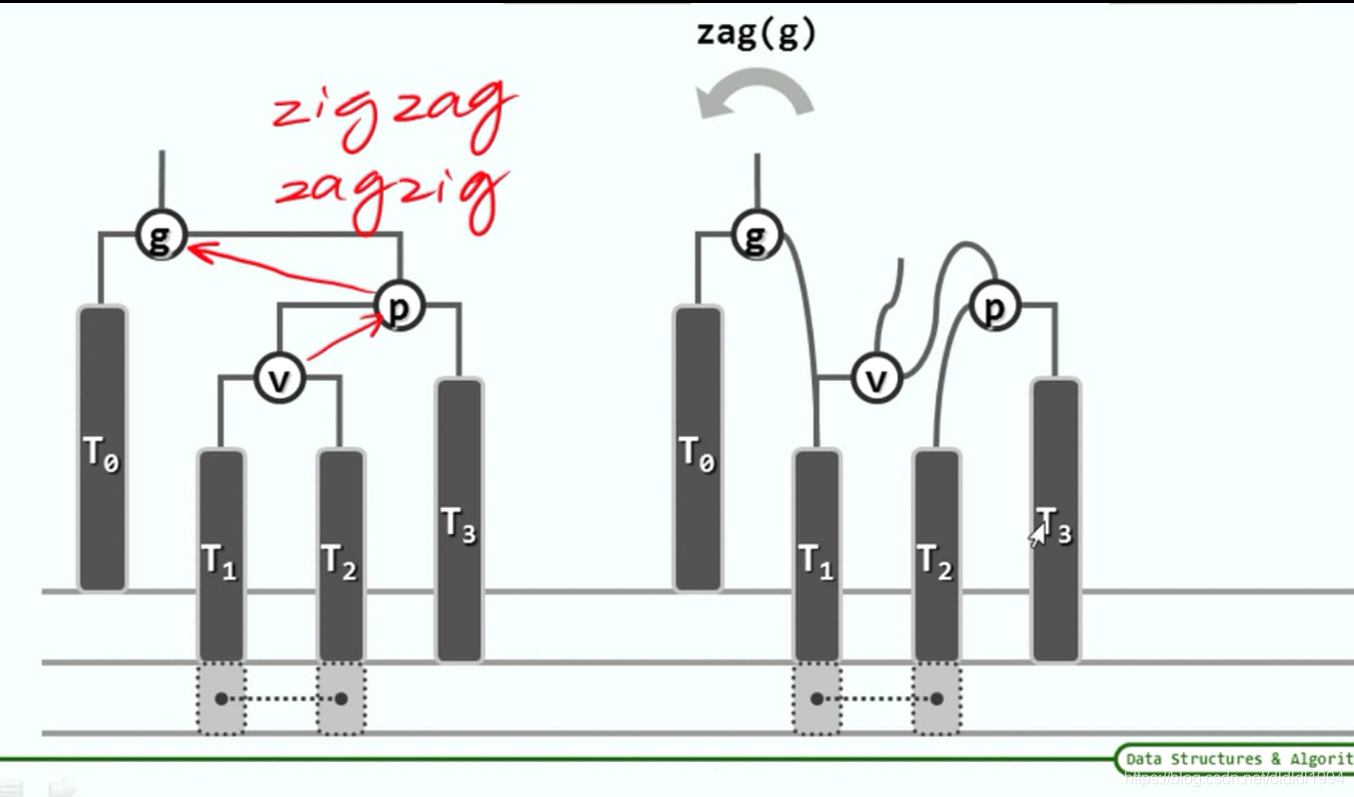
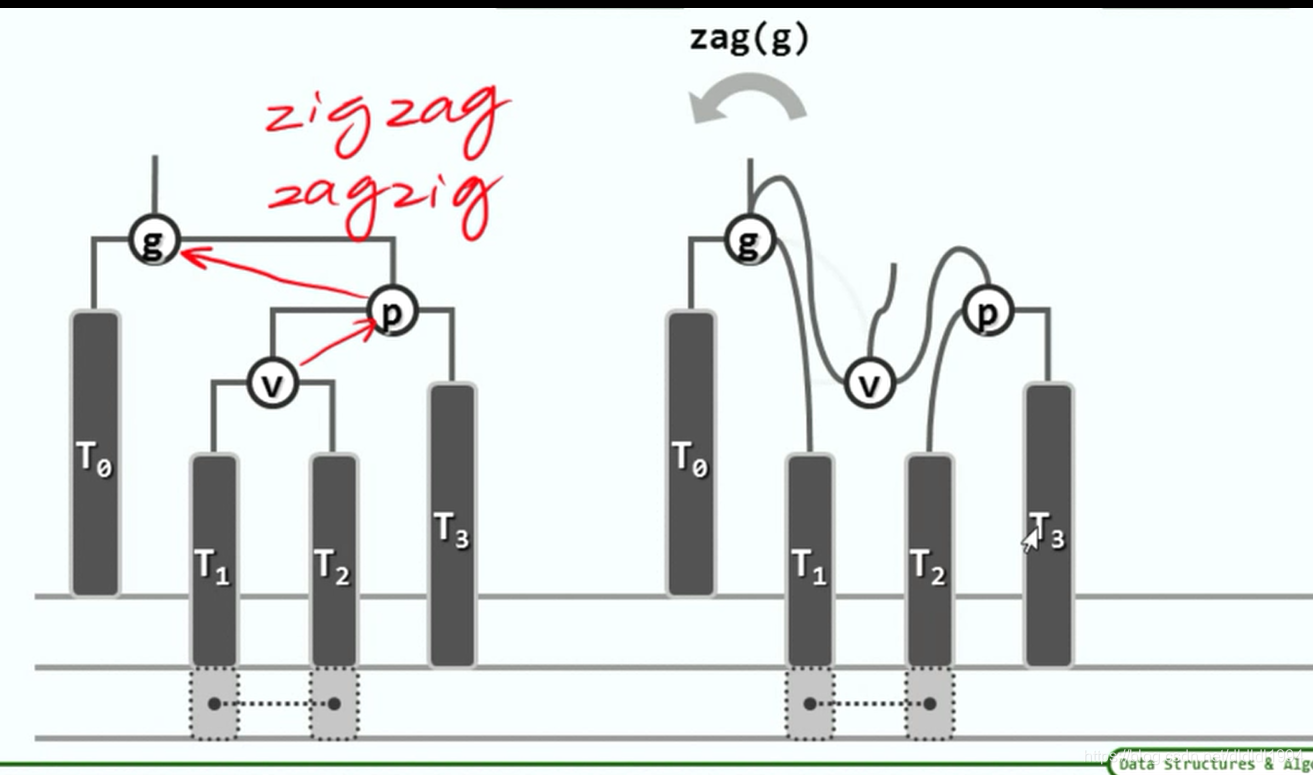
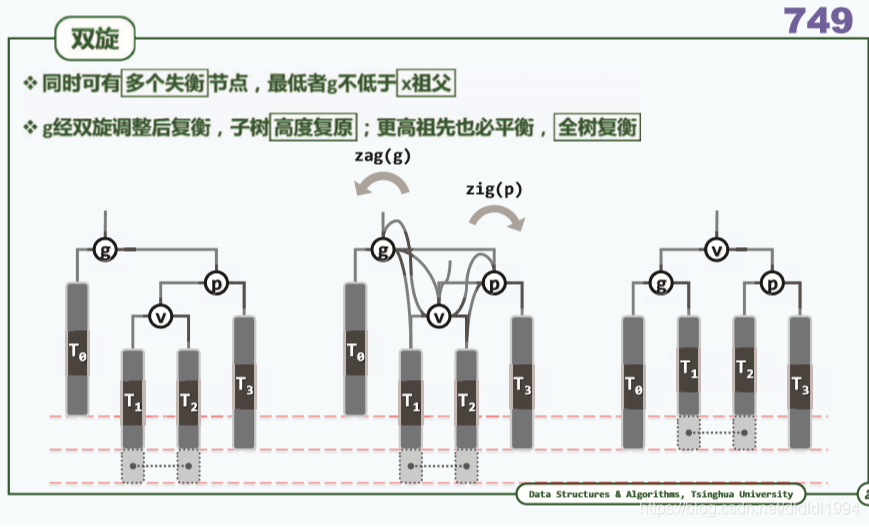
二叉搜索树（AVL树 删除）

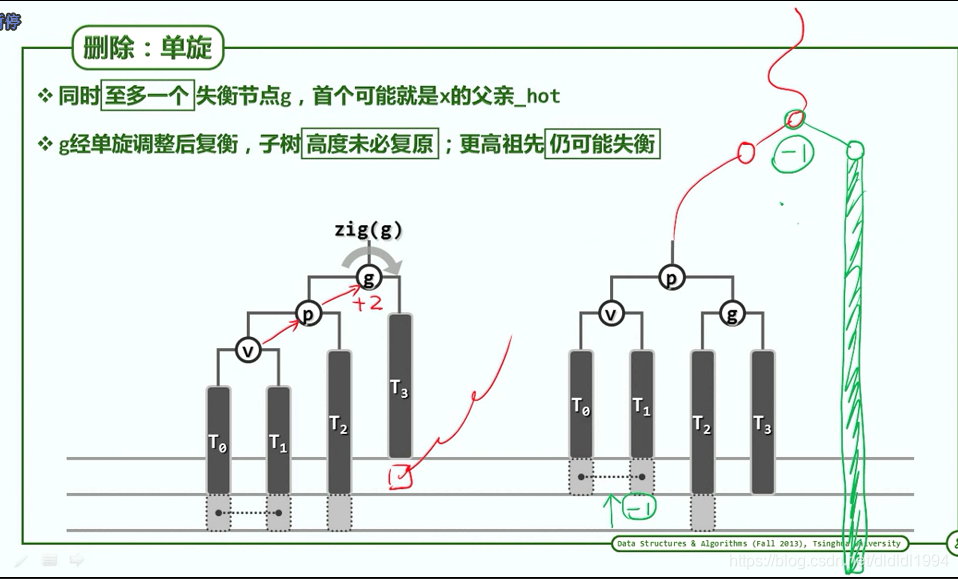
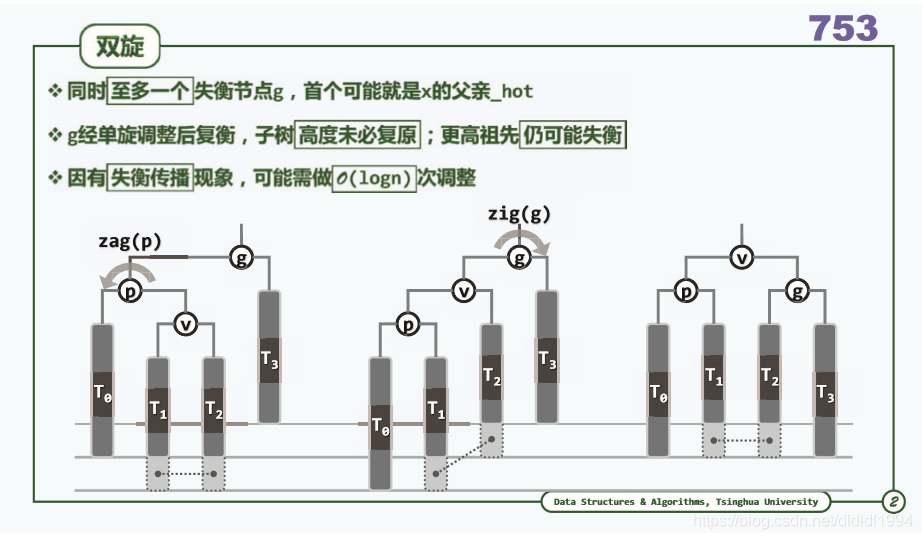
二叉搜索树（AVL树 3+4 重构）

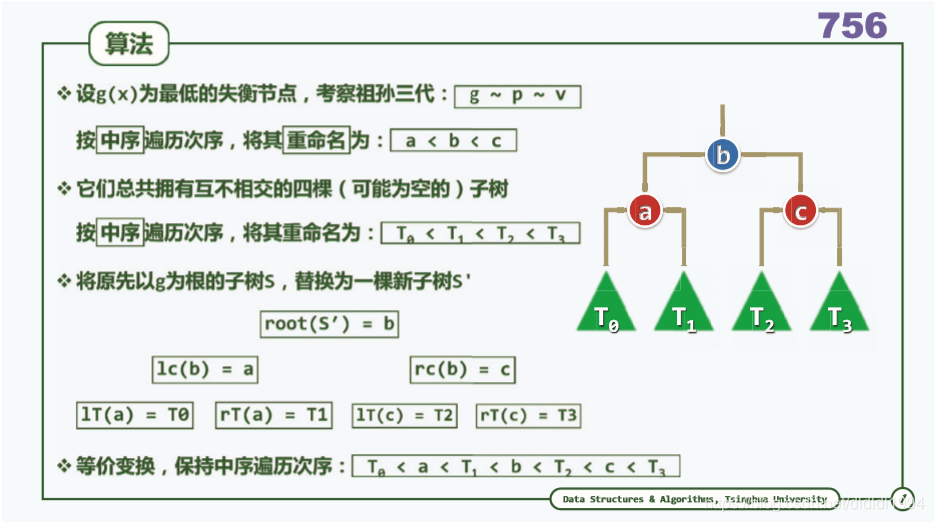
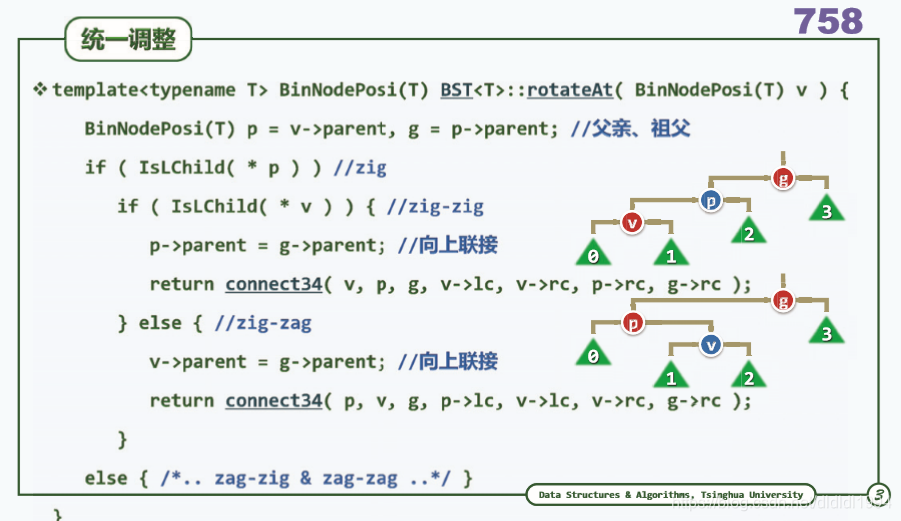
问题：视频里讲解的插入和删除算法可以用于AVL树的任何节点吗？（by wangyanhong11）
答：插入必然会插入到叶节点。因为如果在非叶节点就找到了的话，就会停止插入，报告“已存在”。

删除是可以应用到非叶节点的。删除操作会从删除节点开始，逐层网上检查是否平衡，遇到不平衡的就会进行局部调整，详见视频（by yuantailing 老师）
问题：

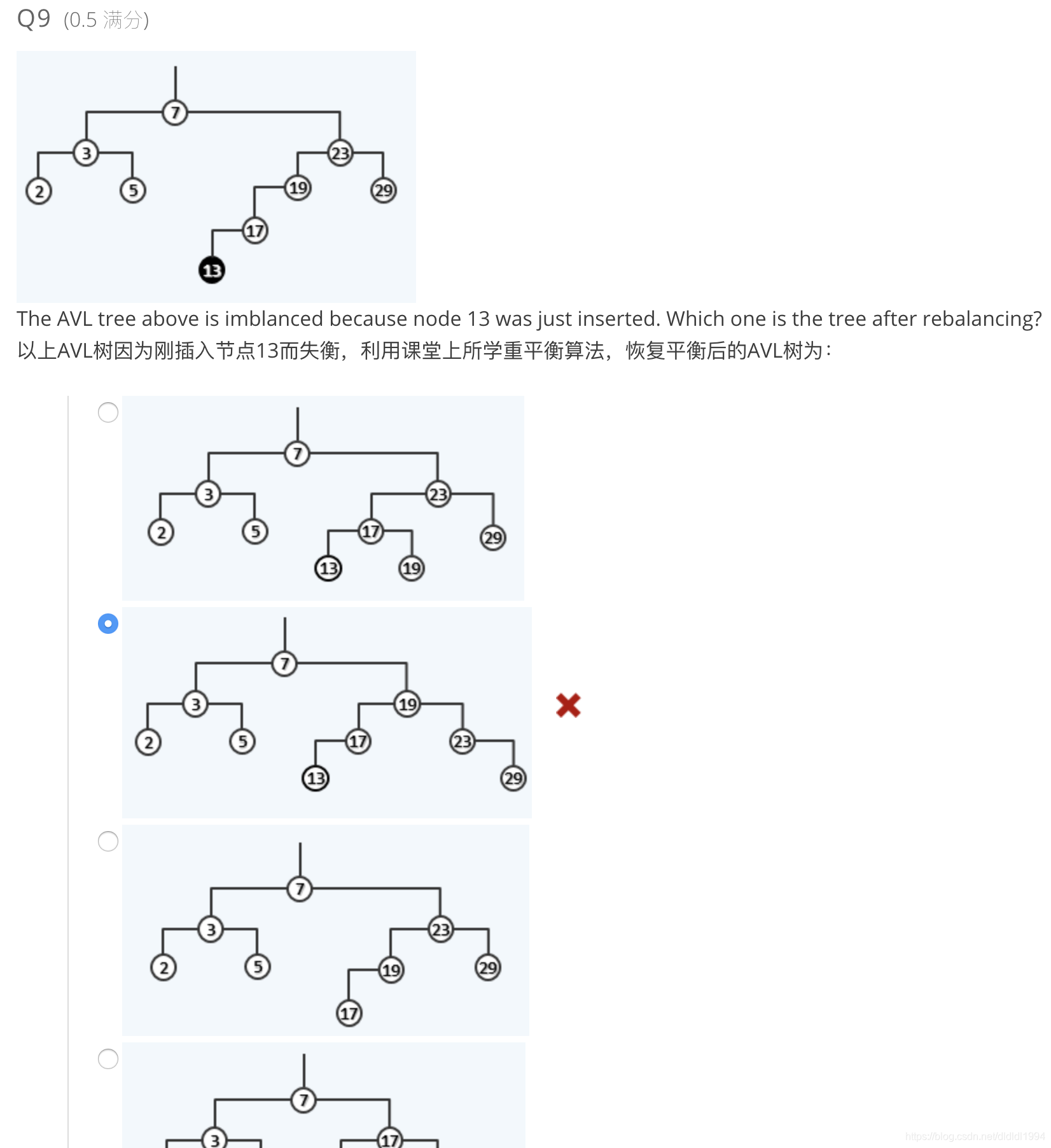
此处v,p,g应分别为17，19，23. 在v17这个子树中插入节点13，故根据重平衡算法，p（19）取代g（23）的地位，依序应为B。 请教一下这个环节是哪里考虑的有问题了呢？（by 小脚丫208688 ）
答：v,p,g是13,17,19（by 不羁的逆袭）