博客介绍了梯度下降算法在监督学习中的应用。损失函数的导数即梯度，求偏导可得各点斜率。目标是让损失最小，通过梯度函数更新参数来实现。对于L2损失，根据梯度正负调整参数以降低loss。
梯度下降算法:
- 监督学习
损失函数的导数称为梯度，若对损失函数的参数求偏导，则这个偏导数代表着损失函数在该参数
下各点的斜率；
目标就是让损失能尽可能的小，希望取到损失函数的最小值，可以通过梯度函数得到损失函数上各点的斜率，然后逐步更新参数从而满足要求的这种方法就是梯度下降！
对于L2损失，参数对应的梯度函数如下：
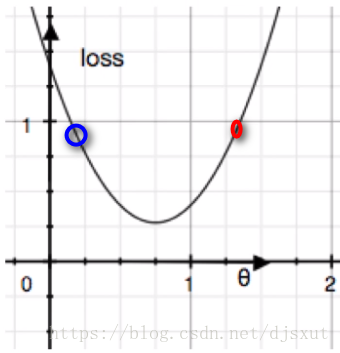
若参数上某一点对应梯度为正值(上图红点)，此时应该减小
，即加上一个负数，从而降低loss；
若参数上某一点对应梯度为负值(上图蓝点)，此时应该增加
，即给
加上一个正数来降低loss；
扫一扫
1275
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
