神经网络与深度学习

回归与分类

线性回归：拟合一个线性函数，用于预测连续数值输出。

损失函数：均方误差（MSE）

对数回归：是分类问题，预测样本属于某个类别的概率，常用于二分类

损失函数：交叉熵损失（Cross Entropy Loss）

二分类问题：输出是两个类别之一（如 0 或 1）

• 常用输出函数：Sigmoid

• 预测逻辑：输出概率大于 0.5 判为正类，否则为负类

• 常用模型：Logistic Regression、SVM、神经网络（输出1个节点+Sigmoid）

多分类问题

• 目标：输出属于多个类别之一（如分类 0/1/2）

• 常用输出函数：Softmax

• 预测逻辑：选取 Softmax 输出中概率最大的类别

• 常用模型：多层感知机（MLP）、CNN、RNN、Transformer等

softmax函数：常用于多分类问题，将多个线性输出变成总和为1的概率分布，常与交叉熵损失一起使用。

感知机：

• 最早的神经网络模型，用于二分类问题

• 结构：线性组合输入 + 激活函数（通常为 sign 函数）
  y=sign(wTx+b)y = sign(w^T x + b)y=sign(wTx+b)

• 工作原理：通过迭代更新权重来将数据线性分割开

• 限制：只能处理线性可分问题，不能解决异或（XOR）等非线性问题

• 扩展：多层感知机（MLP）可解决非线性问题，是现代神经网络的基础

多层感知机（MLP, Multi-Layer Perceptron）

多层感知机是前馈神经网络（Feedforward Neural Network）的一种，由多个感知机（Perceptron)组成，通常包括： 

1. 结构组成

• 输入层（Input Layer）：接受原始特征（如图像像素、文本向量等）。

• 隐藏层（Hidden Layers）：1个或多个隐藏层，每层包含若干神经元，每个神经元接收上一层输出，通过激活函数处理后输出。

• 输出层（Output Layer）：用于输出最终预测值（回归值或分类概率）。

2. 特点

• 每层神经元的输出为：
  a=f(Wx+b)

  • W 是权重矩阵

  • b 是偏置

  • f是激活函数（如 ReLU、Tanh、Sigmoid）

• 通过堆叠多个非线性变换，MLP 可以逼近任意复杂函数（通用逼近定理）。

BP算法（反向传播算法, Backpropagation）

BP 是训练 MLP 的核心算法，用于计算和传播误差，从而更新参数。

1. 原理

BP 算法基于链式法则（Chain Rule），计算损失函数关于每一层权重的梯度，并进行权重更新：

• 正向传播：

  得到预测值y_hat 和损失L(y,y_hat)

• 反向传播：

  • 从输出层开始，反向计算每层的梯度：
    

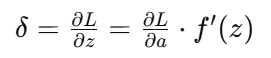
  • 逐层传播误差并更新权重：
    

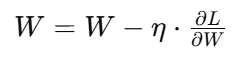
2. BP算法核心步骤

1. 初始化权重和偏置

2. 对每个训练样本：

   • 前向传播计算输出

   • 计算损失（如均方误差或交叉熵）

   • 反向传播误差，计算梯度

   • 更新权重（常结合梯度下降）

3. 优点

• 可训练深层神经网络

• 支持任意层数、任意结构

• 与梯度下降法完美结合

4. 缺点

• 易陷入局部最小值

• 梯度消失或爆炸问题

• 对超参数（学习率、层数、激活函数等）敏感

性能优化

训练常用技巧

1. 模型初始化

   • 均值或高斯分布初始化：将权重限制在 [−1,1]区间。

   • Xavier初始化：保证每层输出的方差一致，信息传播更稳定。

2. 数据划分

   • 训练 / 验证 / 测试 数据按比例分配（如70%/15%/15%）。

   • K折交叉验证：增强泛化能力，减小过拟合风险。

3. 过拟合与欠拟合

   • 欠拟合：训练误差高，模型复杂度不足。

   • 过拟合：训练误差低，测试误差高，模型记忆训练集。

4. 正则化与Dropout

   • 权重衰减（L2正则化）：约束权重大小，抑制过拟合。

   • Dropout：训练时随机丢弃神经元，增强模型鲁棒性。

动量法与病态曲率

1. 病态曲率问题

   在狭窄或陡峭曲率区域（如山沟）梯度下降效率低，震荡严重。

2. 动量法

   • 类比铁球滚动，依靠惯性克服震荡与鞍点困境。

   • 加速收敛，路径更平滑稳定。

自适应梯度算法

1. AdaGrad

   • 每个参数独立调整学习率。

   • 缺点：学习率递减过快，导致后期训练困难。

2. RMSProp

   对梯度历史采用指数衰减平均，保留“近期记忆”，避免AdaGrad的问题。

3. Adam

   • 综合动量法与RMSProp。

   • 同时考虑梯度一阶动量（方向）和二阶动量（幅度），收敛快、稳定性好。