leetcode并查集相关经典题目(思路、分析、代码)

leetcode并查集相关经典题目(思路、分析、代码)

关于并查集的一些基础知识以及应用，可以看我之前的一篇文章：一文搞定并查集
看完那篇文章基本可以完全掌握并查集

547. 朋友圈

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M [i] [j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例 1:
输入: 
[[1,1,0],
 [1,1,0],
 [0,0,1]]
输出: 2 
说明：已知学生0和学生1互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回2。

分析：该题是典型的并查集应用，如果两个人是朋友，则将其归为一类，采用并查集表示，首先初始化，然后遍历，如果两个人是朋友且未在一类则unite。最后查看有多少个集合即可。

• 并：如果两个节点的属于一类，则 并 ，方法是将其中一个节点的根指向另一个节点的根即可
• 查：判断两个节点是否是一类只需要判断他们的根是否相同
• 由于该题的节点数量较少，故没有过多优化。实际上可以添加一个rank数组大致表示节点所在树的高度，当合并时令低树的根指向高树的根可以降低树的高度。

class Solution {
public:
	int par[201]; 
    void init(int n) //初始化并查集
	{
		for(int i=0;i<n;i++)  //让其父结点指向自己 
			par[i]=i;	
	}
	int find(int x) //查找某节点所在树的根节点
	{
		return par[x]==x?x:par[x]=find(par[x]);  //如果自己是根节点则返回，否则向上递归,但是将par[x]指向父亲的根节点(用于优化)	
	} 
	void unite(int x,int y)
	{
		if(find(x)==find(y))//是同一类则返回 
			return;
		else
			par[find(x)]=find(y); //让其中一个节点的根指向另一个节点的根即可 
	}
	int findCircleNum(vector<vector<int>>& M) 
	{
		int row=M.size();
		if(row==0) return 0;
		init(row); //初始化row个节点
		for(int i=0;i<row-1;i++)
		for(int j=i+1;j<row;j++)  //朋友关系是无向的,故只遍历一半即可 
		{
			if(M[i][j]==1)
				unite(i,j);	
		} 
		int result=0;
		for(int i=0;i<row;i++)
			if(par[i]==i) //一个节点是根节点则说明有一个朋友圈 
				result++;
		return result;
		
    }
};

1319. 连通网络的操作次数

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。

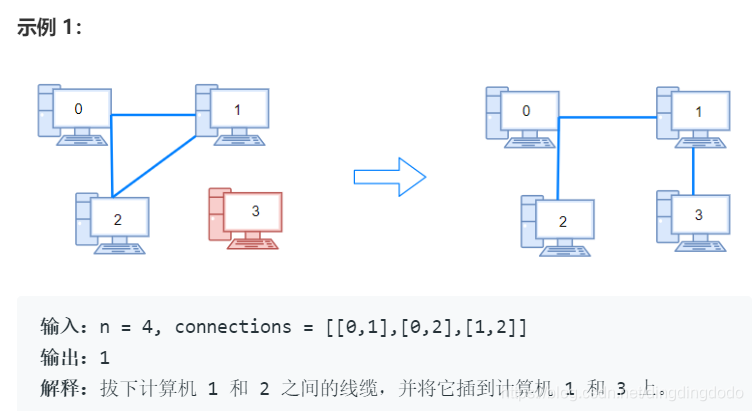
分析：最初的连接中可能存在冗余连接，即一个区域已经形成通路但仍增加了部分连接。并且，最初的连接给定后，理论上是将整个计算机分成了很多"孤岛",可以视作分类。因此，在此可以采用并查集。

• 遍历connections
• 如果当前给定的两个计算机已经连通(已经在一个类)，则不添加这条边，并且记录冗余的连接数量+1
• 当完成并查集建立后，计算网络的类别数量(即孤岛数量)
• 如果冗余连接可以将孤岛全部连接起来，则说明可以完成，理论上最小操作数是 孤岛数量-1.

在此由于节点非常多，因此采用了rank优化。

class Solution {
public:
	vector<int> par;
	vector<int> rank; 
    void init(int n) //初始化并查集
	{
        par.resize(n,0);
		for(int i=0;i<n;i++)
		{	
			par[i]=i; //将每个节点的根指向自身
		}
        rank.resize(n,0);
	}
	int find(int x) //查找某节点所在树的根节点
	{
		return par[x]==x?x:par[x]=find(par[x]);  //如果自己是根节点则返回，否则向上递归,但是将par[x]指向父亲的根节点(用于优化)	
	} 
	void unite(int x,int y)
	{
		int x_par=find(x);
		int y_par=find(y);
		if(x_par==y_par) 
			return; //是同一类，故返回
		//需要合并的话，尽量让rank低的合并到rank高的 
		if(rank[x]<rank[y])
			par[x_par]=y_par; // 
		else
        {
            if(rank[x]==rank[y])  
                rank[x]++; //如果两个树高度一样，则合并后树的高度加1
			par[y_par]=x_par;
        }
    }
	 int makeConnected(int n, vector<vector<int>>& connections) 
	 {
		init(n); //初始化n个节点
		int length=connections.size();
		int more_connections=0; //冗余连接 
		for(int i=0;i<length;i++)
		{
			if(find(connections[i][0])==find(connections[i][1])) //如果已经连通,则冗余
				more_connections++;
			else
				unite(connections[i][0],connections[i][1]); //否则合并 
		}
		int set_nums=0;
		for(int i=0;i<n;i++) //查看孤岛数量
		{
			if(par[i]==i)
				set_nums++;
		}
		return set_nums-1<=more_connections?set_nums-1:-1; 
     }	
};

990. 等式方程的可满足性

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一：“a==b” 或 “a!=b”。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

示例 1：
输入：["a==b","b!=a"]
输出：false
解释：如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个方程。没有办法分配变量同时满足这两个方程。

示例 2：
输出：["b==a","a==b"]
输入：true
解释：我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。

示例 3：
输入：["a==b","b==c","a==c"]
输出：true

分析：将相等的变量放置在一起，如果没有与之矛盾的不等式语句，就说明该方程是可以满足的。因此，采用并查集的方法，将相等的变量进行分类。

• 遍历等式，将相等的变量归为一类,如果等式两边的两个变量已经是一类，则忽略即可
• 遍历不等式，如果不等式两端的两个变量是一类的，则返回false，否则说明该不等式可以成立

由于节点数量较少，故在此不考虑根据高度进行压缩。

class Solution {
public:
    vector<int> par; //字母共26个
    void init() //初始化
    {
        par.resize(27,0);
        for(int i=0;i<26;i++)
            par[i]=i;
    }
    int find(int x) //查找根
    {
        return par[x]==x?x:par[x]=find(par[x]);
    }
    void unite(int x,int y)//进行合并
    {
        par[find(x)]=find(y);
    }
    bool equationsPossible(vector<string>& equations) 
    {
        init();
        for(int i=0;i<equations.size();i++)
        {
            if(equations[i][1]=='=') //只取等式
            {
                int x=equations[i][0]-'a';
                int y=equations[i][3]-'a';
                if(find(x)!=find(y))
                    unite(x,y);
            }
        }
        for(int i=0;i<equations.size();i++)
        {
            if(equations[i][1]=='!') //只取不等式
            {
                int x=equations[i][0]-'a';
                int y=equations[i][3]-'a';
                if(find(x)==find(y)) //说明x和y相等,但这里x和y不等,故false
                    return false;
            }
        }
        return true;
    }
};

128. 最长连续序列

给定一个未排序的整数数组，找出最长连续序列的长度。

要求算法的时间复杂度为 O(n)。

示例:
输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。

分析：该题也可以采用并查集，实际上该题用并查集是比较巧妙的。

如果数字是连续的，则将其归为一类，则最终我们的目的就是找到最长的那个类的长度。

由于数组中数字是非连续的，因此如何设置并查集？可以采用unordered_map,首先遍历数组将所有元素存储到unordered_map中，然后便可以每次判断相邻数字是否存在于unordered_map中，如果在，则将其合并，只需要维护一端即可(每次判断该数字+1是否在即可)。为了更快的找到类的长度，可以建立一个映射，每次merge时可以将根对应的value+1，说明该类的元素数量+1，维护最大的数量即可。

class Solution {
public:
    unordered_map<int,int> par; //存储节点到父结点的映射关系
    unordered_map<int,int> count;  //存储每个节点对应的类的长度
    void init(vector<int> &nums)
    {
        for(auto i:nums)
        {
            par[i]=i; //父结点指向自己
            count[i]=1; //每个类都是1
        }
    }
    int find(int x)
    {
        return x==par[x]?x:par[x]=find(par[x]);
    }
    int unite(int x,int y) //在此让返回合并后类的大小
    {
        int x_par=find(x);
        int y_par=find(y);
        if(x_par==y_par) //属于一类
            return count[y_par];
        else
        {
            par[x_par]=y_par; //让x对应的根指向y对应的根
            count[y_par]+=count[x_par]; //合并后的根的count为两个和
            return count[y_par];
        }
    }
    int longestConsecutive(vector<int>& nums) 
    {
        if(nums.size()==0) return 0;
        init(nums); //初始化
        int result=1;
        for(auto i:nums)
        {
            if(par.count(i+1)>0) //说明i+1在数组
                result=max(result,unite(i,i+1));
        }
        return result;

    }
};