Topcoder SRM 693 & Atcoder RC#56 小结

最新推荐文章于 2021-02-27 15:59:12 发布

转载最新推荐文章于 2021-02-27 15:59:12 发布 · 157 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/naturepengchen/articles/5617673.html

本文解析了两道编程竞赛题目：一是构造特定完备匹配数的二分图；二是通过状态压缩动态规划解决团队分组问题。提供了清晰的思路与代码实现。

2016-06-26 12:17:54

近期打的两场比赛，小结一下里面有趣的题。

1：TC SRM 693 div1 600pt

题意：给出一个k（<=1e9），让你造一个n（<=20）对点的二分图，点之间可以有重边，总边数为E（<=120），使得其完备匹配方案数为k。

思路：首先注意到可以有重边，这个很关键。其次，这种构造显然是拆分 k 为某个 base 进制，由于只有20对点，考虑用3进制，接下来yy一下。

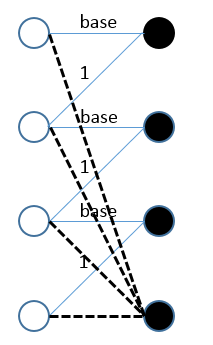
※ 如下建图，边权即为该边建立的重边数。

※ 那么最右下角的黑点，就可以决定各个进制为上的数字了。

※ 比如最右下黑点与最左下白点建立 a 条边，就能构造出 a * base^3，以此类推。

※ 可以发现一旦最右下黑点与第 i 个白点匹配，那么 i+1 ~ n 号白点只能沿着斜向的边匹配 i ~ n-1 号黑点，而 1 ~ i-1 号白点可以匹配对应的黑点，形成 base^(i-1)。因此进制之间不冲突，形成加法关系。

class BipartiteConstruction {
    public:
    vector <int> construct(int K) {
        vector<int> ans;
        ans.PB(20);
        for(int i = 0; i < 19; ++i) 
            for(int j = 0; j < 3; ++j) ans.PB(i * 20 + i);
        for(int i = 1; i < 20; ++i) ans.PB(i * 20 + i - 1);
        for(int i = 0; i < 20; ++i){
            int v = K % 3;
            for(int j = 0; j < v; ++j) ans.PB(i * 20 + 19);
            K /= 3;
        }
        return ans;
    }
};

View Code

2：Atcoder RC#56 C题

题意：给你n（<=17）个人和一个常数K，第 i 个人与第 j 个人之间有合作值 wij，让你给他们分组，使得最后的评价最高，评价计算方法：分的组数 * K - ∑（wij | i 和 j 不在同一组）

思路：ok，n 很小，考虑状压，一开始我的考虑是二维，但发现比较繁琐而且没有必要。所以定义 dp[s] 为 s 状态下的最优解，s 代表已经给哪些人安排了分组。

※转移： dp[s] = dp[f] + Val(f ^ s) + K，f 是 s 的真子集，f ^ s 表示集间差（表示新的一组取的人），Val( ts ）计算的是集合 ts 内每个人两两之间的合作值和。

※用记忆化来做的话需要枚举真超集，for(int f = (s + 1) | s; f < (1 << N); f = (f + 1) | s)，可以用方便的超集枚举法。

int N,K;
int G[20][20];
int P[MAXN];
int dp[MAXN];
 
int Solve(int s){
    if(s == (1 << N) - 1) return 0;
    if(dp[s]) return dp[s];
    int ans = 0;
    for(int f = (s + 1) | s; f < (1 << N); f = (f + 1) | s){
        int ts = s ^ f;
        ans = max(ans,K + Solve(f) + P[ts]);
    }
    return dp[s] = ans;
}
 
int main(){
    int sum = 0;
    scanf("%d%d",&N,&K);
    for(int i = 0; i < N; ++i){
        for(int j = 0; j < N; ++j){
            scanf("%d",&G[i][j]);
            sum += G[i][j];
        }
    }
    sum /= 2;
    int top = 1 << N;
    for(int s = 0; s < top; ++s){
        for(int i = 0; i < N; ++i) if(s & (1 << i)){
            for(int j = i + 1; j < N; ++j) if(s & (1 << j)){
                P[s] += G[i][j];
            }
        }
    }
    printf("%d\n",Solve(0) - sum);
    return 0;
}

View Code

转载于:https://www.cnblogs.com/naturepengchen/articles/5617673.html