K-MEANS

一、K-均值聚类（K-means）

k-means算法是一种简单的迭代型聚类算法，采用距离作为相似性指标，从而发现给定数据集中的K个类，且每个类的中心是根据类中所有值的均值得到，每个类用聚类中心来描述。对于给定的一个包含n个d维数据点的数据集X以及要分得的类别K,选取欧式距离作为相似度指标，聚类目标是使得各类的聚类平方和最小，即最小化：

 　　　　　　　                                             　

结合最小二乘法和拉格朗日原理，聚类中心为对应类别中各数据点的平均值，同时为了使得算法收敛，在迭代过程中，应使最终的聚类中心尽可能的不变。

 

二、算法步骤

K-means是一个反复迭代的过程，算法分为四个步骤：

1） 选取数据空间中的K个对象作为初始中心，每个对象代表一个聚类中心；

2） 对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类；

3） 更新聚类中心：将每个类别中所有对象所对应的均值作为该类别的聚类中心，计算目标函数的值；

4） 判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回2）。

 

三、实例

# -*- coding: UTF-8 -*-
import numpy
import random
import matplotlib.pyplot as plt
 

def calculateDistance(vecA, vecB):   
 
    return numpy.sqrt(numpy.sum(numpy.square(vecA - vecB)))

def findCentroids(data_get, k):    
 
    return random.sample(data_get, k)
 
 
def minDistance(data_get, centroidList):
 
    clusterDict = dict()  
    for element in data_get:
        vecA = numpy.array(element)  
        flag = 0  
        minDis = float("inf")  
 
        for i in range(len(centroidList)):
            vecB = numpy.array(centroidList[i])
            distance = calculateDistance(vecA, vecB)  
            if distance < minDis:
                minDis = distance
                flag = i  
 
        if flag not in clusterDict.keys():  
            clusterDict[flag] = list()
        clusterDict[flag].append(element)  
 
    return clusterDict  

 
 
def calculate_Var(clusterDict, centroidList):
   
    sum = 0.0
    for key in clusterDict.keys():
        vecA = numpy.array(centroidList[key])
        distance = 0.0
        for item in clusterDict[key]:
            vecB = numpy.array(item)
            distance += calculateDistance(vecA, vecB)
        sum += distance
 
    return sum

def getCentroids(clusterDict):
 
    centroidList = list()
    for key in clusterDict.keys():
        centroid = numpy.mean(numpy.array(clusterDict[key]), axis=0)
        centroidList.append(centroid)
 
    return numpy.array(centroidList).tolist()

 
 
def showCluster(centroidList, clusterDict):
 
    colorMark = ['or', 'ob', 'og', 'ok', 'oy', 'ow']  
    centroidMark = ['dr', 'db', 'dg', 'dk', 'dy', 'dw']  
    for key in clusterDict.keys():
        plt.plot(centroidList[key][0], centroidList[key][1], centroidMark[key], markersize=12)  
        for item in clusterDict[key]:
            plt.plot(item[0], item[1], colorMark[key])  
 
    plt.show()
 
 
data = [[0.0, 0.0], [3.0, 8.0], [2.0, 2.0], [1.0, 1.0], [5.0, 3.0],
        [4.0, 8.0], [6.0, 3.0], [5.0, 4.0], [6.0, 4.0], [7.0, 5.0]]

if __name__ == '__main__':
 
    centroidList = findCentroids(data, 3)  
    clusterDict = minDistance(data, centroidList)  
    newVar = calculate_Var(clusterDict, centroidList)  
    oldVar = -0.0001  
 
    print('***** 第1次迭代 *****')
    for key in clusterDict.keys():
        print('聚类中心: ', centroidList[key])
        print('对应聚类: ',clusterDict[key])
    print('平均均方误差: ', newVar)
    showCluster(centroidList, clusterDict)  
 
    k = 2
    while abs(newVar - oldVar) >= 0.0001:  
        centroidList = getCentroids(clusterDict)  
        clusterDict = minDistance(data, centroidList)  
        oldVar = newVar
        newVar = calculate_Var(clusterDict, centroidList)
 
        print('***** 第%d次迭代 *****' % k)
 
        for key in clusterDict.keys():
            print('聚类中心: ', centroidList[key])
            print('对应聚类: ', clusterDict[key])
        print('平均均方误差: ', newVar)
        showCluster(centroidList, clusterDict)  
 
        k += 1

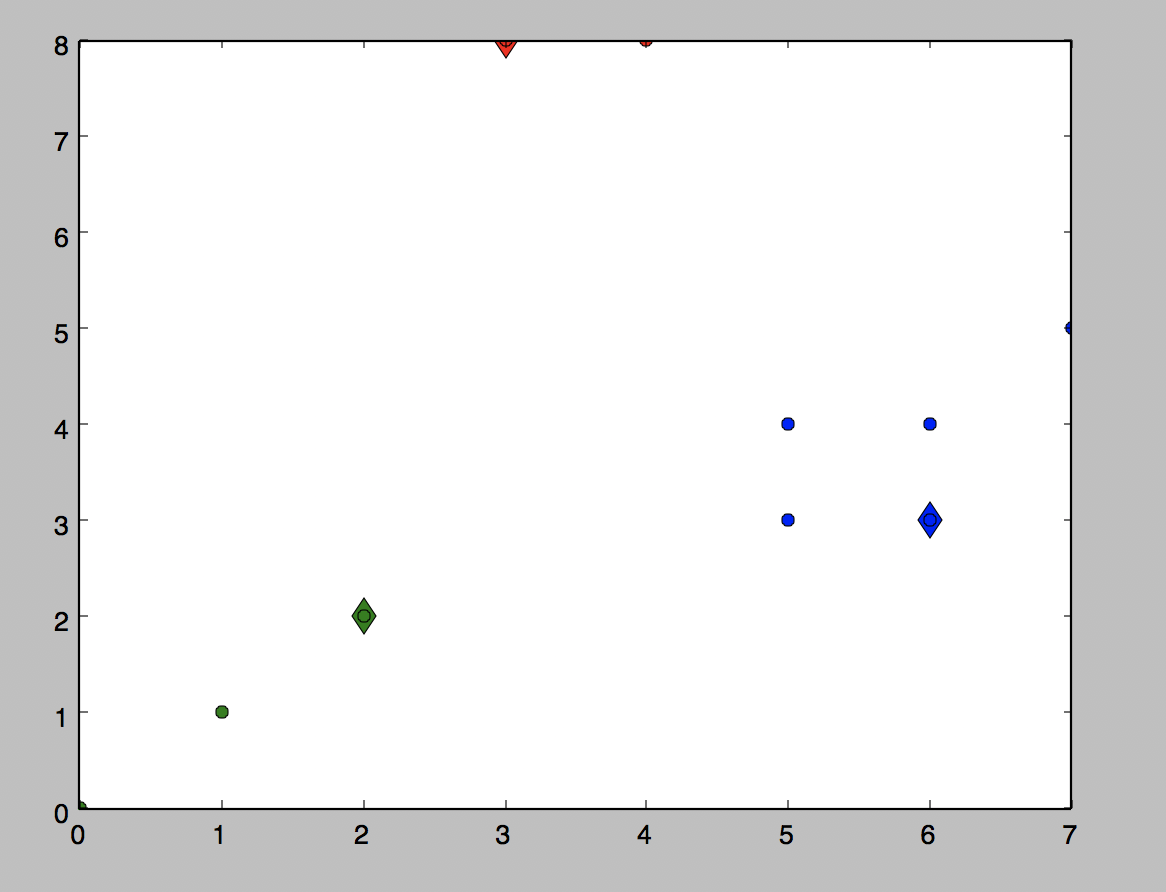
结果：

 

 

转载于:https://www.cnblogs.com/UniqueColor/p/10996269.html