卷积神经网络

卷积神经网络(CNN)

Relu激活函数

定义

不同于之前在全连接前馈神经网络中用到的sigmoid函数，这里我们要使用一个新的激活函数，也就是Relu激活函数：

\[f(x)= max(0,x)\]

图像如下：

意义

相对于sigmoid激活函数，Relu激活函数有几个优势：

1. 速度快，只需要计算一个\(\max(0,x)\)。
2. 减轻了梯度消失的问题，回忆一下计算梯度的公式：\(\nabla=\sigma'\delta x\)。这里的\(\sigma'\)是sigmoid函数的导函数，而且这个导函数最大值只能取到1/4。所以说每计算一个sigmoid函数的导函数，梯度都会越来越小，这对于深层神经网络来说会导致一个很致命的问题，也就是所谓的梯度消失问题。而Relu函数的导函数是1，不会导致梯度变小。
3. 稀疏性，Relu函数在自变量取值小于等于0的时候是不激活的，而神经科学对大脑的研究也表明，大脑在工作的时候大约只有5%神经元是激活的。比起sigmod，使用Relu函数的神经网络激活率更低。

卷积层

这里要介绍的就是卷积神经网络中最重要的一个部分了，就是因为有了卷积层所以才叫卷积神经网络。

定义

卷积神经网络一般是用于图像处理，如果把图像的所有像素作为输入，那么这个输入数量和特征量是非常巨大的，卷积的核心思想就是通过一个过滤器把图像的特征抽取出来并降低输入数量。
下面来讲解一个具体的计算过程：

图中的各个图像的说明：

• 左边为image，即输入图像，大小为5*5。
• 中间为filter，即进行卷积操作的矩阵，大小为3*3。
• 右边为feature map，卷积操作后得到的特征矩阵，大小为3*3。

符号定义：

• \(x_{i,j}\)表示image的\(i\)行\(j\)列元素。
• \(w_{i,j}\)表示filter的\(i\)行\(j\)列权重。
• \(a_{i,j}\)表示feature map的\(i\)行\(j\)列元素。
• \(f\)表示激活函数

那么卷积的计算方法就是：

\[a_{i,j}=f(\sum_{m=0}^{2}\sum_{n=0}^{2}w_{m,n}x_{i+m,j+n}+w_b)\]

以\(a_0\)为例就是：

\[\begin{align} a_{0,0}&=f(\sum_{m=0}^{2}\sum_{n=0}^{2}w_{m,n}x_{m+0,n+0}+w_b)\\ &=relu(w_{0,0}x_{0,0}+w_{0,1}x_{0,1}+w_{0,2}x_{0,2}+w_{1,0}x_{1,0}+w_{1,1}x_{1,1}+w_{1,2}x_{1,2}+w_{2,0}x_{2,0}+w_{2,1}x_{2,1}+w_{2,2}x_{2,2}+w_b)\\ &=relu(1+0+1+0+1+0+0+0+1+0)\\ &=relu(4)\\ &=4 \end{align}\]

计算结果如下图：

整个卷积的计算过程可以看下面这个动画：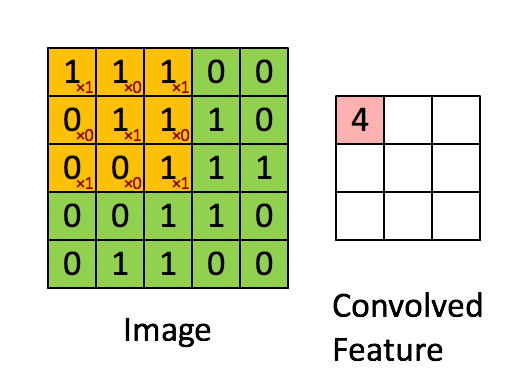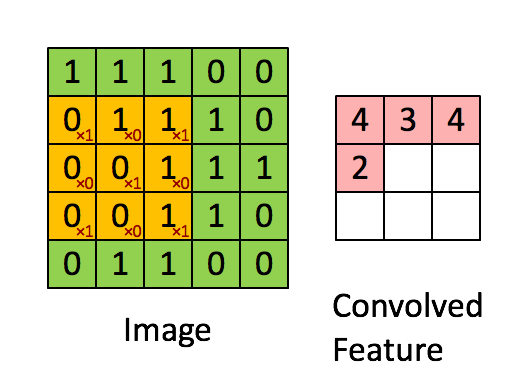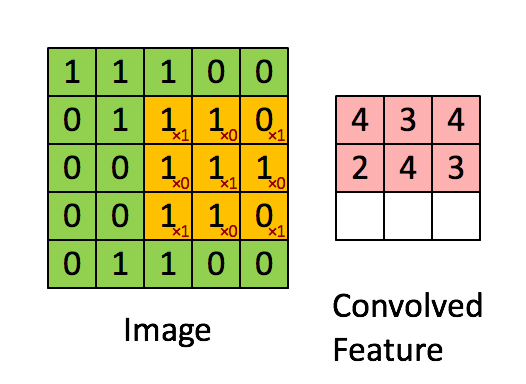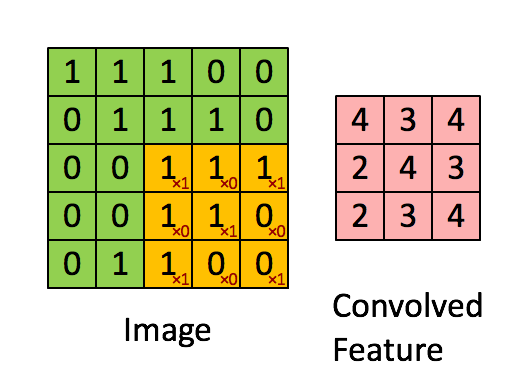

注意以上的的卷积计算过程做了两个重要的简化：

1. 步幅(stride)1为1，步幅即filter每次移动的格数，步幅变大的话，feature map是会变小的。有关stride高度和宽度的两个公式：\[\begin{align}W_2 &= (W_1 - F + 2P)/S + 1\\H_2 &= (H_1 - F + 2P)/S + 1\end{align}\]其中\(P\)为Zero Padding就是在原image矩阵的周围填充的0。\(W_1\)和\(H_1\)为卷积前的高宽。
2. 频道(channel)为1，即图像是有深度度，因为计算机中的图像一般是RGB来存储的，是三个颜色通道叠加的结果。如果channel不为1，卷积层的计算公式为：\[a_{i,j}=f(\sum_{d=0}^{D-1}\sum_{m=0}^{F-1}\sum_{n=0}^{F-1}w_{d,m,n}x_{d,i+m,j+n}+w_b)\]其中的D为深度，F为filter的大小，因为图像是方的，所以高宽一样。

下图就是完整卷积的计算过程了：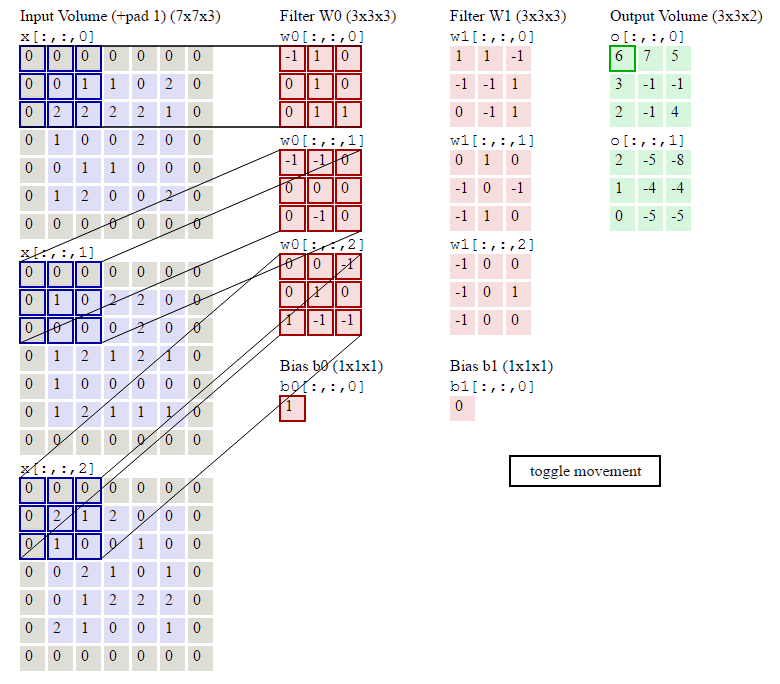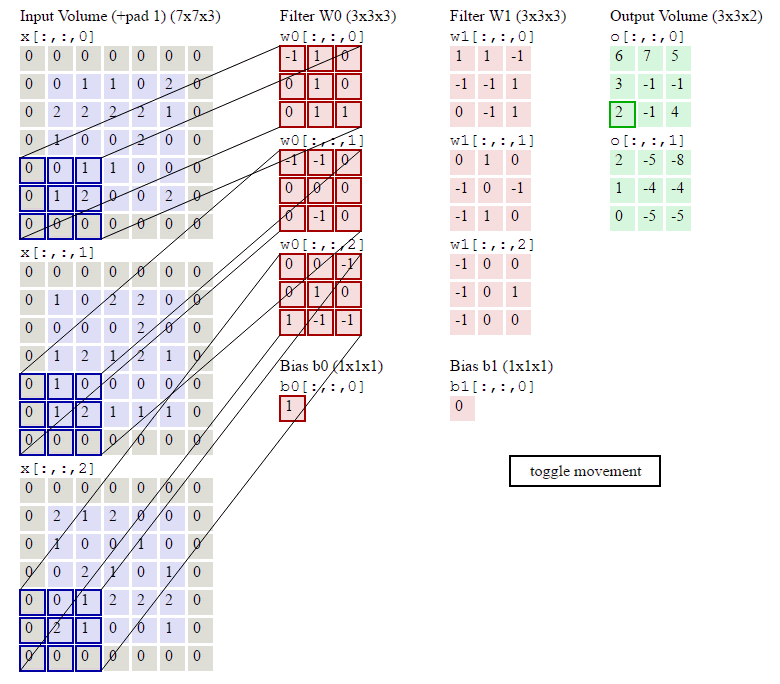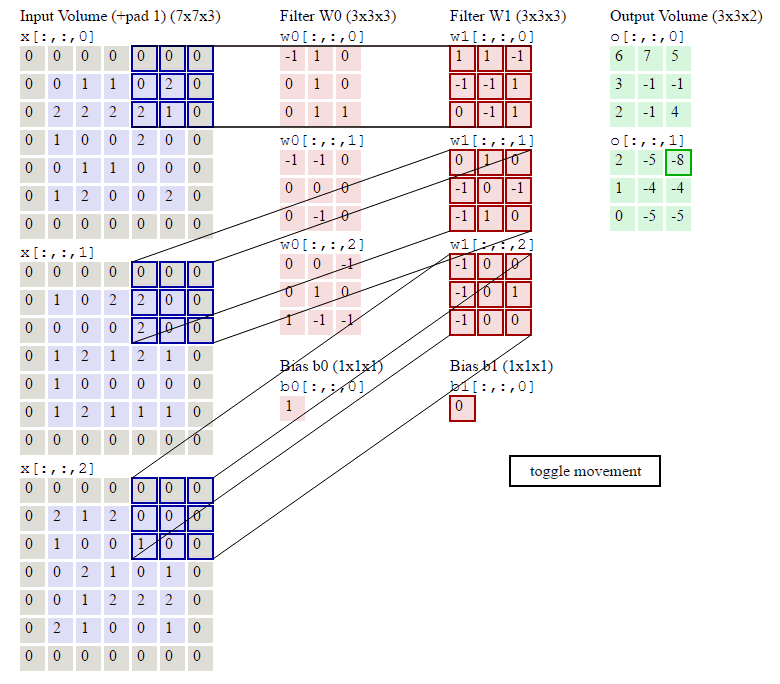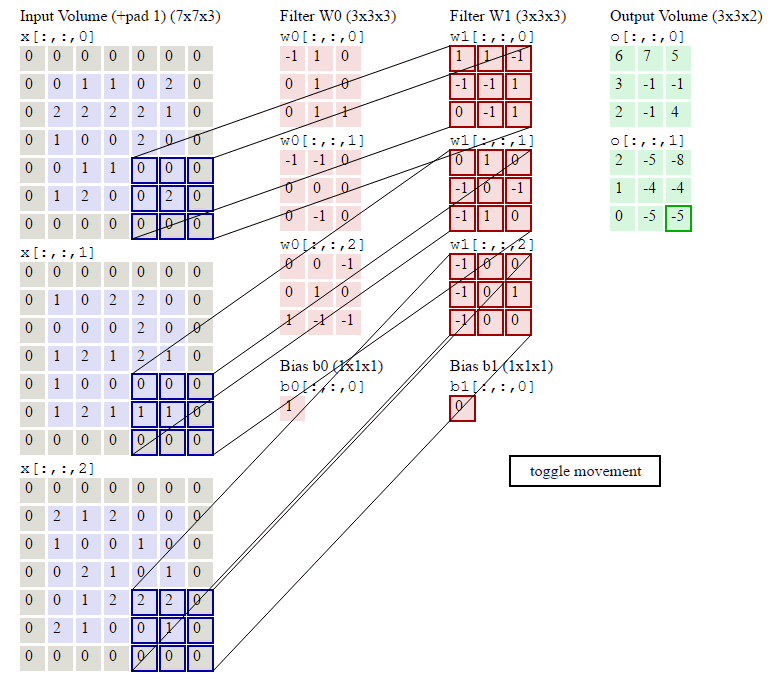

意义

在讲解卷积层计算的时候稍微提了一下卷积层意义，这里稍微详细地说明一下。
深度学习最大的意义便在于自动化的特征处理，因为只要网络够深，抽象能力足够强，是可以免于人工提取特征的。而卷积对于图像的特征的提取是非常有效的。这里强调一下，是针对图像而言的特征提取，对于其他领域可能并没那么好用。
还有另一方面是减少了参数个数，比如一个5*5的图像，如果全连接隐层有九个节点，那么权值的数量就是5*5*9个，而对于卷积层只有一个3*3的卷积矩阵而已。

池化层

计算

池化(Pooling)层最常用的池化方法是最大池化(Max Pooing)。即：

选择这个区域内最大的那个值即可。上图是2*2 Max Pooling的示例。

意义

那么池化层的意义在哪呢。池化层的主要作用其实是下采样，去掉Feature Map中不重要的样本来进一步减少参数数量。

基本构架

上图是一个很经典的CNN构架，基本来说就是：
输入->卷积->池化->卷积->池化->全连接层->输出。
通过将输入不断的卷积和池化抽取输入的特征最后连接到一个全连接层进行输出。卷积和池化层堆叠的越多一般来说神经网络的抽象能力也越好。

训练

CNN中有两个地方是需要训练的，一个是卷积层的权重，一个全连接的权重。全连接层权重的训练方法已经在之前讲过了，这里稍微提一下卷积层的训练方法。
训练参考参考1中的内容。

参考

1. 零基础入门深度学习(4) - 卷积神经网络

转载于:https://www.cnblogs.com/nevermoes/p/cnn.html