机器学习——线性判别分析

什么是线性判别分析

引自周志华老师的《机器学习》

线性判别分析是一种经典的线性学习方法，给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能的近，异类样例的投影点尽可能原，在对新样本进行分类时，将其投影到同样的这条直线上，在根据投影点的位置来确定新样本的类别

一个直观的例子：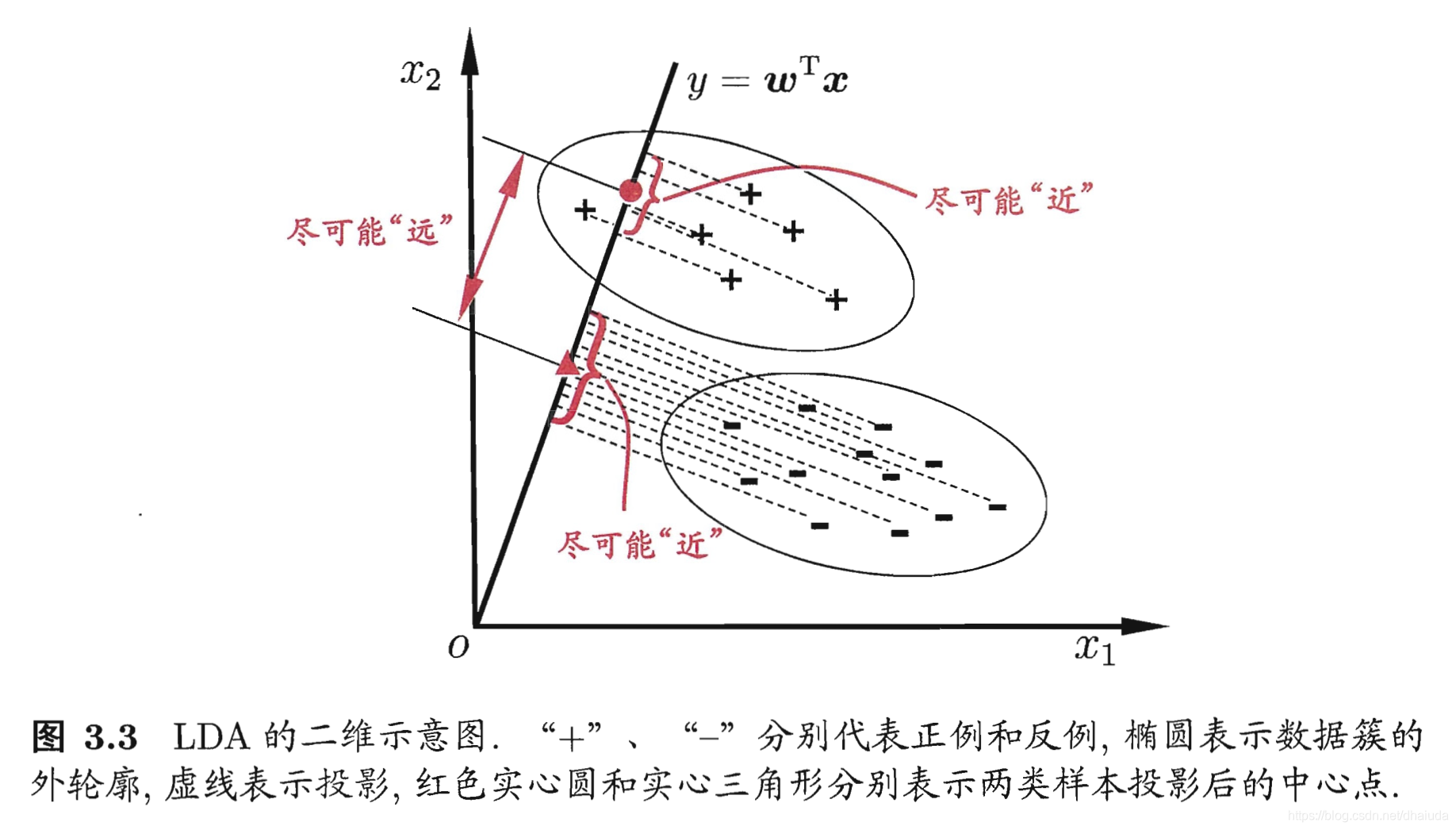

线性判别分析的作用

1、分类
2、降维，其将高维空间的点映射到一条直线上，用一个实数来表示高维空间的点，此时点的描述信息会会全部丢失，例如用三个维度（形状、甜度、颜色）来描述苹果，有一个苹果在这三个维度的得分为（1，2，3），则可以用（1，2，3）来表述这个苹果的特征，利用线性判别分析投影到直线后，我们用一个实数来表示这个苹果，但是我们无法知道苹果的甜度是多少

基本思想

线性判别分析具有两个关键点

• 1、投影后，不同类别的点尽可能远离
• 2、投影后，相同类别的点尽可能靠近

对于关键点1，我们可以使用投影后，不同类别的中心点之间的距离来衡量，中心点距离越远，类别之间的区分度越高

对于关键点2，我们可以使用方差来衡量投影后同类别点之间的散乱程度（方差的统计意义便是衡量点与点之间的散乱程度），方差越小，投影后同类别的数据之间越靠近

如何将点投影到直线上

周志华老师的《机器学习》一书并没有明显说明如何将点投影到直线上，那么我们如何用式子去刻画点投影到直线这个动作呢？

我们来看看维基百科对于线性回归的定义 我是链接：

线性判别分析 (LDA)是对费舍尔的线性鉴别方法的归纳，这种方法使用统计学，模式识别和机器学习方法，试图找到两类物体或事件的特征的一个线性组合，以能够特征化或区分它们

LDA试图通过特征的线性组合来特征化或区分它们，若特征为（$x_1$,$x_2$,…,$x_d$），那么LDA的输出应该是

$$\begin{array}{r}y=w_1{x}_1+w_2{x}_2+...+w_d{x}_d\end{array}\text{\hspace{1em}(1.0)}$$

令$w$=($w_1$,$w_2$,…,$w_d$)，x=（$x_1$,$x_2$,…,$x_d$），则式1.0可重写为

$$\begin{array}{r}y=w^{T}x\end{array}\text{\hspace{1em}(1.1)}$$

式1.1可看成是向量$w$与向量$x$的点乘，向量点乘可以写成：$w^T\ast x$=|$w$||$x$|cos$\theta$，其几何意义为向量$x$在向量$w$方向的投影长度的|$w$|倍，投影的直线为向量$w$所在方向的直线，可见线性判别分析不是把点投射到直线上，而是将点投射到直线后。在拉长|$w$|倍，由于所有的投影点都拉长了|$w$|倍，所以点与点之间的相对位置不变（虽然点与点的距离发生了变化，但只要相对位置不变，影响就不会很大）。线性判别分析用投影长度来刻画投影后点的位置。

二分类线性判别分析

接下来的任务就是如何使用式1.1去刻画第二节所述的两个关键点，我们从一个例子入手

假设我们现有一个问题——判断一个工厂生产的零件是不是好零件，一个零件只有好和坏之分，因此这是一个二分类问题，设一个零件具有d个特征，假设我们有一批样本数据，
好零件的样本为:$（x_{11},x_{12},...,x_{1d}）,（x_{21},x_{22},...,x_{2d}）,...,（x_{n1},x_{n2},...,x_{nd}）$
坏零件的样本为:$（x_{11}^{\prime },x_{12}^{\prime },...,x_{1d}^{\prime }）,（x_{21}^{\prime },x_{22}^{\prime },...,x_{2d}^{\prime }）,...,（x_{n1}^{\prime },x_{n2}^{\prime },...,x_{nd}^{\prime }）$

好零件与坏零件都有n个样本。

如何刻画类别的中心点之间的距离

线性判别分析使用均值来刻画类别中心点，好零件的均值向量$\overline{x}$为

$$（\frac{{\sum }_{i=1}^n{x}_{i1}}{n}，\frac{{\sum }_{i=1}^n{x}_{i2}}{n}，.....，\frac{{\sum }_{i=1}^n{x}_{id}}{n}）$$

投影后，各样本的值为

$$\sum _{i=1}^d{w}_i{x}_{1i}，\sum _{i=1}^d{w}_i{x}_{2i}，...，\sum _{i=1}^d{w}_i{x}_{ni}$$

投影后，样本的均值为

$$\begin{array}{r}\frac{{\sum }_{i=1}^d{w}_i{x}_{1i}+{\sum }_{i=1}^d{w}_i{x}_{2i}+...+{\sum }_{i=1}^d{w}_i{x}_{ni}}{n}\end{array}\text{\hspace{1em}(1.2)}$$

1.2可变为：

$$\begin{array}{r}\frac{w_1{\sum }_{i=1}^n{x}_{i1}}{n}+\frac{w_2{\sum }_{i=1}^n{x}_{i2}}{n}+...+\frac{w_d{\sum }_{i=1}^n{x}_{id}}{n}\end{array}\text{\hspace{1em}(1.3)}$$

1.3可变为：

$$\begin{array}{r}（w_1，w_2，...，w_d{）}^T\ast （\frac{{\sum }_{i=1}^n{x}_{i1}}{n}，\frac{{\sum }_{i=1}^n{x}_{i2}}{n}，.....，\frac{{\sum }_{i=1}^n{x}_{id}}{n})\Rightarrow w^T\overline{x}\end{array}\text{\hspace{1em}(1.4)}$$

同理可得坏零件的均值为：

$$\begin{array}{r}{w}^T\overline{x^{\prime }}\end{array}\text{\hspace{1em}(1.5)}$$

类别的中心点之间的距离可以通过下列式子进行刻画

$$\begin{array}{r}(w^T\overline{x}-w^T\overline{x^{\prime }}{)}^2\Rightarrow w^T(\overline{x}-\overline{x^{\prime }})(\overline{x}-\overline{x^{\prime }}{)}^{T}w\end{array}\text{\hspace{1em}(1.6)}$$

如何刻画投影后相同类别的散乱程度

对于好零件来说，令$x_i$表示$（x_{i1},x_{i2},...,x_{id}）$，投影后的方差为：

$$\sum _{i=1}^n(w^T{x}_i-w^T\overline{x}{)}^2=\sum _{i=1}^n(w^T(x_i-\overline{x})(x_i-\overline{x}{)}^{T}w)$$

由于矩阵的加法与乘法满足分配率，所以上式可以变为：
$$w^T(\sum _{i=1}^n(x_i-\overline{x})(x_i-\overline{x}{)}^T)w\text{\hspace{1em}(1.7)}$$

同理可得坏零件投影后的的方差为

$$w^T(\sum _{i=1}^n(x_i^{\prime }-\overline{x^{\prime }})(x_i^{\prime }-\overline{x^{\prime }}{)}^T))w\text{\hspace{1em}(1.8)}$$

将式1.7与式1.8相加得：

$$\begin{array}{rl}& w^T(\sum _{i=1}^n(x_i-\overline{x})(x_i-\overline{x}{)}^T))w+w^T(\sum _{i=1}^n(x_i^{\prime }-\overline{x^{\prime }})(x_i^{\prime }-\overline{x^{\prime }}{)}^T))w\\ =& w^T(\sum _{i=1}^n(x_i^{\prime }-\overline{x^{\prime }})(x_i^{\prime }-\overline{x^{\prime }}{)}^T+\sum _{i=1}^n(x_i-\overline{x})(x_i-\overline{x}{)}^T)w\end{array}\text{\hspace{1em}(1.9)}$$

由于${\sum }_{i=1}^n(x_i-\overline{x})(x_i-\overline{x}{)}^T)$和${\sum }_{i=1}^n(x_i^{\prime }-\overline{x^{\prime }})(x_i^{\prime }-\overline{x^{\prime }}{)}^T$为标量，所以式1.9取最小值时，1.7与1.8也具有最小值

如何用式1.9与式1.6刻画LDA的两个关键点

令$S_b$表示$(\overline{x}-$$\overline{x^{\prime }})$$(\overline{x}-$$\overline{x^{\prime }}{)}^T$,$S_w$表示$({\sum }_{i=1}^n(x_i^{,}-\overline{x^{\prime }})(x_i^{\prime }-\overline{x^{\prime }}{)}^T+{\sum }_{i=1}^n(x_i-\overline{x})(x_i-\overline{x}{)}^T)$,先明确一点，$S_b$与$S_w$均为标量，$S_b$为类间散度矩阵，$S_w$为类内散度矩阵

线性判别分析具有的两个关键点为

• 1、投影后，不同类别的点尽可能远离，令式1.6最大化
• 2、投影后，相同类别的点尽可能靠近，令式1.9最小化

因此，线性判别法的最终关键点为求下列函数的最大值

$$J=\frac{w^T{S}_{b}w}{w^T{S}_{w}w}$$

此时我们已经将问题转换为函数极值问题了，这里使用拉格朗日乘子法求解，我们将分母限制为长度为1（这是用拉格朗日乘子法一个很重要的技巧），则有：

$$\begin{array}{rl}c& =w^T{S}_{b}w-\lambda (w^T{S}_{w}w-1)\\ & =S_b(w_1^2+w_2^2+....+w_d^2)-\lambda [S_w(w_1^2+w_2^2+....+w_d^2)]+\lambda \end{array}$$

极值处的导数为0，函数$s$对$w$求偏导有：

$$\begin{gathered} \frac{\partial c}{\partial w_1}=2w_1{S}_b-2\lambda w_1{S}_w \\ \frac{\partial c}{\partial w_2}=2w_2{S}_b-2\lambda w_2{S}_w \\ ...... \\ \frac{\partial c}{\partial w_d}=2w_1{S}_b-2\lambda w_1{S}_w \end{gathered}$$

令上述式子等于0，则有
$$2S_{b}w-2\lambda S_{w}w=0\Rightarrow S_{b}w=\lambda S_{w}w$$
$S_{b}w$其实为

$$(\overline{x}-\overline{x^{\prime }})(\overline{x}-\overline{x^{\prime }}{)}^{T}w$$

$(\overline{x}-$$\overline{x^{\prime }}{)}^{T}w$为标量，我们设它为${\lambda }_w$，则有

$${\lambda }_w(\overline{x}-\overline{x^{\prime }})=\lambda S_{w}w\Rightarrow S_w^{-1}(\overline{x}-\overline{x^{\prime }})=\frac{\lambda }{\lambda w}w$$

其实 $S_w^{-1}(\overline{x}-$$\overline{x^{\prime }})$就是最优解，假设$w_1$是最优解，则$S_w^{-1}(\overline{x}-$$\overline{x^{\prime }})$为$\frac{\lambda }{\lambda w}{w}_1$，我们把$\frac{\lambda }{\lambda w}{w}_1$代入函数$J$，会发现参数$\frac{\lambda }{\lambda w}$被约掉了，所以$S_w^{-1}(\overline{x}-$$\overline{x^{\prime }})$就是最优解

---

如果您想了解更多有关深度学习、机器学习基础知识，或是java开发、大数据相关的知识，欢迎关注我们的公众号，我将在公众号上不定期更新深度学习、机器学习相关的基础知识，分享深度学习中有趣文章的阅读笔记。