代码随想录算法训练营第四天 | 24. 两两交换链表中的节点、19.删除链表的倒数第N个节点、面试题 02.07. 链表相交、142.环形链表II

24. 两两交换链表中的节点

题目

求解

两两交换链表中的节点，设置虚拟头节点辅助求解，当对节点进行位置变化时，需要知道该节点的上一个节点和下一个节点。

以tmp->before->after->nextBefore该部分链表为例，说明交换节点的操作。交换后的结果应为tmp->after->before->nextBefore，nextBefore是下一组需要进行交换的节点中靠前的一个。

进行交换的条件

当前节点位置后至少存在两个节点，才需要继续交换，即tmp.next && tmp.next.next

交换的先后顺序

交换顺序的时候不能丢失后面的节点，因此先连接after节点后面的部分，即before.next = after.next。

接着交换after和before的位置，即after.next = before，并与前面的部分连接tmp.next=after，完成本次交换

将tmp更新为下次需要交换的两个节点前面的位置，也就是此时的before

代码实现

var swapPairs = function(head) {
    // 交换两个相邻的节点
    let dummyHead = new ListNode(0,head);
    let tmp = dummyHead; // tmp指向需要交换的两个节点的前一个节点
    while(tmp.next && tmp.next.next){ // 停止的条件？
        // 交换
        let before = tmp.next, after= tmp.next.next;
        before.next = after.next;
        after.next = before;
        tmp.next = after;
        tmp = before;
    }
    return dummyHead.next;
};

19.删除链表的倒数第N个节点

题目

求解

如何找到倒数第n个节点（双指针）

采用双指针的形式，快慢指针间距离为n，当快指针为null时，慢指针即是倒数第n个节点

首先使快慢指针距离为n

let dummyHead = new LinkNode(0,head), fast = slow = dummyHead;
while(n--){
    fast = fast.next;
}

接着同时移动快慢指针，即可在快指针到达null时，使慢指针到达倒数第n个节点

while(fast){
    fast = fast.next;
    slow = slow.next;
}

由于需要删除倒数第n个节点，因此应找到倒数第n+1个节点。根据上述思想，当fast.next === null时，慢指针为倒数第n+1个节点

while(fast.next){
    fast = fast.next;
    slow = slow.next;
}

代码

var removeNthFromEnd = function(head, n) {
    let dummyHead = new ListNode(0,head),fast=slow=dummyHead;
    // 找到倒数第n个节点的前一个节点，倒数第n+1个节点
    while(n--){
        fast = fast.next;
    }
    while(fast.next!==null){
        fast = fast.next;
        slow = slow.next;
    }
    slow.next = slow.next.next;
    return dummyHead.next;
};

易错部分

在定义快慢指针时，应采用fast=slow=dummyHead而不能let fast = new ListNode(0,head),slow = new ListNode(0,head);

原因：

采用第二种定义时，在删除的节点是头节点时会出错。

因为在操作中改变的是slow的下一个节点，dummyHead仍指向原来的头节点

面试题 02.07. 链表相交

题目

求解

给定两个不同的链表，求两链表相交的起点

首先分析题目，需要找到两个节点的共同部分，公共部分的长度一定是一致的，所以当两个链表的长度不相等时，例如链表A比链表B长，只需要将链表A后部分里和链表B长度一致的部分与链表B的节点进行比较即可。

首先比较两链表长度，构建一个函数求解链表长度

var getListLen = function(head){
    let len = 0;
    let dummyHead = new ListNode(0,head),tmp=dummyHead;
    while(tmp.next){
        len++;
        tmp=tmp.next;
    }
    return len;
}

比较两个链表的长度，并且为了方便后续操作，令链表A表示更长的链表。也就是说如果lenA<lenB，对链表A和链表B进行交换

// let curA = headA, curB = headB;
if(lenA<lenB){
    [headA, headB] = [headB, headA];
    [lenA, lenB] = [lenB, lenA];
}

使节点curA指向链表A和链表B对齐的位置

let i = lenA - lenB;
while(i--){
    curA = curA.next
}

比较两链表剩余部分即可，在走到链表尾部或两链表存在相同节点时停止

while(curA && curA !== curB){
    curA = curA.next;
    curB = curB.next;
}

代码

var getIntersectionNode = function(headA, headB) {
    let lenA = getListLen(headA), lenB = getListLen(headB);
    let curA = headA, curB = headB;
    if(lenA<lenB){ // 求得谁是更长的链表，并以dummyHeadA表示它的虚拟头节点，lenA是它的长度
        [curA,curB] = [curB,curA];
        [lenA,lenB] = [lenB,lenA];
    }
    let count = lenA - lenB;
    while(count--){
        curA = curA.next; 
    }
    while(curA && curA !== curB ){
        curA = curA.next;
        curB = curB.next;
    }
    return curA;
};
var getListLen = function(head){
    let len = 0;
    let dummyHead = new ListNode(0,head),tmp=dummyHead;
    while(tmp.next){
        len++;
        tmp=tmp.next;
    }
    return len;
}

142.环形链表II

题目

求解（双指针）

定义快慢指针，快指针fast每次走两步，慢指针slow每次走一步，如果存在环，则快慢指针一定会相遇（跑步套圈）

当链表为空或只存在一个节点时不可能有环。

借助图形表示快慢指针走过的距离

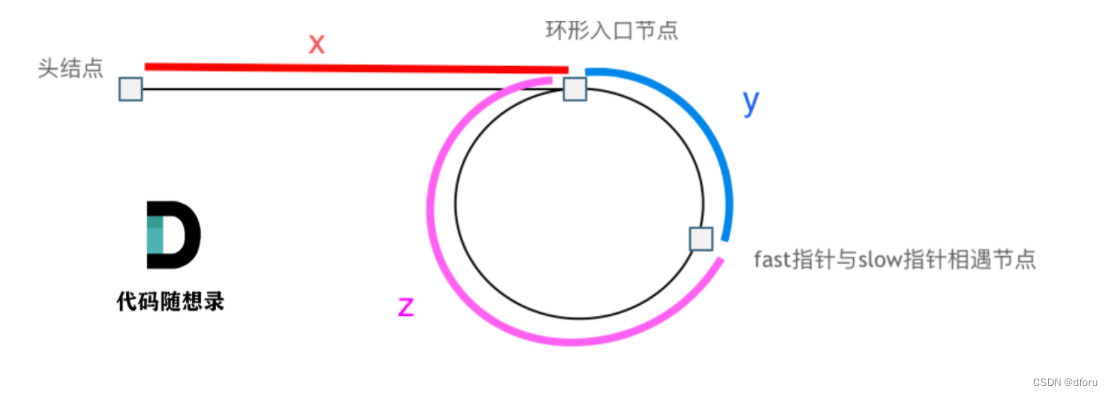
如果有环，则快慢指针相遇的结点距环的入口的距离为z。此时，快指针比慢指针多走了n(n>=1)圈，慢指针一定是第一圈（当慢指针进入环时，快指针一定已经在环里，慢指针走完一圈时，快指针已经走了两圈，一定已经相遇）

此时，慢指针走过的距离为x+y，快指针走过的距离为x+y+n(y+z)

根据快慢指针的距离，有2(x+y)=x+y+n(y+z)，即x = n(y+z) - y = (n-1)(y+z) + z

当n=1时，x=z，也就是说头节点到入口节点的距离等于相遇节点到入口节点的距离，因此只需要知道快慢指针相遇的位置

定义快慢指针

let slow = head.next, fast = head.next.next;

快慢指针能否相遇？如果能，找到位置

// 当快指针为null，或者快指针的下一个节点为null时，说明没有环。若有环，找到相遇位置
// 由于快指针每次走两步，因此需要先确定快指针的下一个节点存在，才有必要令快指针前进
while(fast && fast.next && fast !== slow){ 
    fast = fast.next.next;  
    slow = slow.next;
} 
// 判断此时是没有环 还是找到相遇位置了
if(fast! || !fast.next){ // 没有环，快指针走到链表尾部
    return null;
}

代码

var detectCycle = function(head) {
    if(!head || !head.next){
        return null;
    }
    // 快指针每次前进两步，需要判断fast.next是否存在
    let slow = head.next, fast = head.next.next;
    // 找到快慢指针在环里相遇的位置
    // 如果没有环的话，fast或fast.next有可能是null，没有环不可能相遇
    while(fast && fast.next && fast!==slow){
        fast = fast.next.next;
        slow = slow.next;
    }
    // 判断有没有环
    if(!fast||!fast.next){
        return null;
    }
    slow = head;
    while(slow!==fast){
        slow = slow.next;
        fast = fast.next;
    }
    return slow;
};