代码随想录算法训练营第十六天 | 104.二叉树的最大深度、111.二叉树的最小深度、222.完全二叉树的节点个数

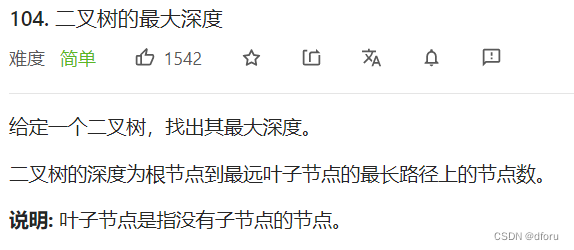
104.二叉树的最大深度 （优先掌握递归）

题目

求解

迭代法 - 层序遍历

层序遍历，记录遍历的层数

代码

var maxDepth = function(root) {
    let depth = 0;
    let queue = [];
    if(!root){return depth}
    queue.push(root);
    while(queue.length){
        let len = queue.length;
        for(let i=0;i<len;i++){
            let node = queue.shift();
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
        depth +=1;  // 深度 + 1
    }
    return depth;
};

递归法

1. 输入：根节点；输出：深度

2. 终止条件：空节点null

3. 单层递归内容：max(左子树深度,右子树深度)+1

代码

var maxDepth = function(root) {
    // 递归法
    if(!root){return 0}
    return 1+Math.max(maxDepth(root.left),maxDepth(root.right));
};

111.二叉树的最小深度 （优先掌握递归）

题目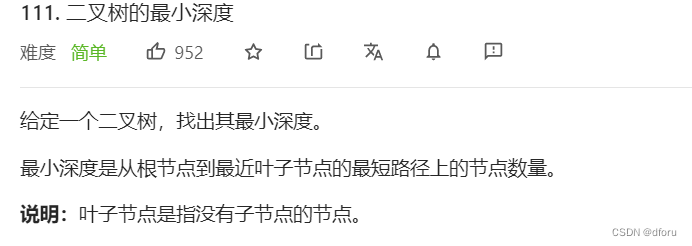

求解

迭代 - 层序遍历

逐层遍历，当出现叶节点时停止遍历，返回此时的深度

代码

var minDepth = function(root) {
    // 最小深度
    let depth = 0;
    let queue = [];
    if(!root){return depth}
    queue.push(root);
    while(queue.length){
        let len = queue.length;
        depth += 1;
        for(let i=0;i<len;i++){
            let node = queue.shift();
            if(!node.left && !node.right){
                return depth;
            }
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
};

递归

1. 输入：根节点；输出：深度

2. 终止条件：空节点null

3. 单层递归内容：

   • 左右子树为空，深度为1

   • 左子树/右子树为空，右子树/左子树深度+1

   • 左右子树都不为空，min(左子树深度,右子树深度)+1

代码

var minDepth = function(root) {
    // 递归
    // 1. input : node, return: depth
    // 2. 终止 : !node
    // 3.
    if(!root){return 0}
    if(!root.left && !root.right){return 1}
    if(!root.left){return 1+minDepth(root.right)}
    if(!root.right){return 1+minDepth(root.left)}
    return 1+Math.min(minDepth(root.left),minDepth(root.right));
};

222.完全二叉树的节点个数（优先掌握递归）

题目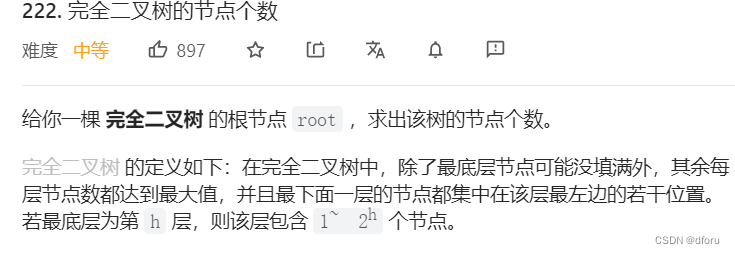

求解

迭代 - 层序遍历

记录每层节点个数

代码

var countNodes = function(root) {
    // 迭代 层序遍历
    let count = 0;
    let queue = [];
    if(!root){return 0}
    queue.push(root);
    while(queue.length){
        let len = queue.length;
        count += len;
        for(let i=0;i<len;i++){
            let node = queue.shift();
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return count;
};

递归

常规二叉树节点的计算

1. 输入：节点；输出：以该节点为根节点的二叉树的节点数量

2. 终止条件：空节点

3. 单层递归内容：左子树的节点数量+右子树的节点数量+1

代码

var countNodes = function(root) {
    // 递归
    // 普通二叉树
    if(!root){return 0}
    return countNodes(root.left) + countNodes(root.right) + 1;
};

完全二叉树节点的计算

递归到某一深度一定会有左孩子或者右孩子为满二叉树

1. 输入：节点；输出：以该节点为根节点的满二叉树的节点数量

2. 终止条件：空节点null

3. 单次递归的内容：

   • 判断是否是满二叉树：通过比较左右子树深度

   • 是满二叉树：节点数量为2^h-1

代码

var countNodes = function(root) {
    // 递归
    // 完全二叉树
    // 根据左子树和右子树的深度 判断是否满二叉树
    if(!root){return 0;}
    let leftDepth = 0,
        rightDepth = 0;
    let leftNode = root.left,
        rightNode = root.right;
    while(leftNode){
        leftDepth++;
        leftNode = leftNode.left;
    }
    while(rightNode){
        rightDepth;
        rightNode = rightNode.right;
    }
    if(leftDepth == rightDepth){return ((2<<leftDepth)-1)}
    return countNodes(root.left) + countNodes(root.right) +1;
};