Ｄｅｅｐ ｌｅａｒｎｉｎｇ ( 1 )

   今天开始学习 Machine   Learning，接下来还有 Deep Learning  & Pattern Recognition ，为机器视觉方面知识的系统学习做准备。

   相关知识

   分布函数：

   分布函数（cumulant distribution function,cdf）是概率统计中重要的的函数，正是通过它，可用数学分析的方法来研究随机变量。

设X是一个 随机变量，x是任意 实数，函数   称为X的分布函数。有时也记为X~F(x)

对于任意实数

   

,  

 

因此，若已知X的分布函数，就可以知道X落在任一 区间(x1,x2]上的 概率，在这个意义上说，分布函数完整地描述了随机变量的 统计规律性。

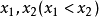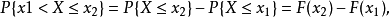
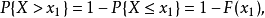
如果将X看成是数轴上的随机点的坐标，那么，分布函数F(x)在x处的 函数值就表示X落在区间(-∞,x]上的概率。

F(x)为随机变量X的分布函数，其充分必要条件为

(1)（非降性）

 

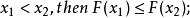
(2)(有界性）

 

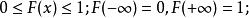
(3)右连续性

   

;

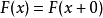联合分布：

随机变量X和Y的联合分布函数是设(X,Y)是二维随机变量，对于任意实数x,y，二元函数：F(x,y) = P{(X<=x) 交 (Y<=y)} => P(X<=x, Y<=y)称为二维          随机变量(X,Y)的分布函数。

设E是一个随机试验，它的样本空间是S={e}。设X=X(e)和Y=Y(e)是定义在S上的随机变量，由它们构成的一个向量（X,Y），叫做二维随机向量或        二维随机变量。

设(X,Y)是二维 随机变量，对于任意实数x,y， 二元函数：

F(x,y) = P{(X<=x) 交 (Y<=y)} => P(X<=x, Y<=y)

称为： 二维随机变量(X,Y)的 分布函数，或称为随机变量X和Y的联合分布函数

联合概率分布的几何意义

如果将 二维 随机变量(X,Y)看成是平面上随机点的坐标，那么 分布函数F(x,y)在(x,y)处的 函数值就是随机点(X,Y)落在以点(x,y)为顶点而位于该点左         下方的无穷矩形域内的 概率。

对离散随机变量而言，联合分布概率 密度函数为Pr(X = x & Y = y)，即

P(X=x and Y=y)=P(Y=y∣X=x)P(X=x)=P(X=x∣Y=y)P(Y=y)= P(X<=xi, Y<yi)

因为是概率分布函数，所以必须有

∑x∑yP(X=x and Y=y)=1

   互信息：

      互信息(Mutual Information)是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随       机变量由于已知另一个随机变量而减少的不肯定性。

设两个随机变量

   

的联合分布为

   

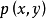，边际分布分别为

   

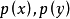，互信息

   

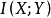是联合分布

   

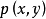与乘积分布

   

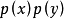的相          对熵，即

互信息与多元 对数 似然比检验以及皮尔森

   

校验有着密切的联系。

信息的含义

信息是 物质、能量、信息及其属性的标示。逆维纳信息定义

信息是 确定性的增加。逆香农信息定义

信息是 事物现象及其属性标识的集合。

互信息的含义

信息论中的互信息

一般而言，信道中总是存在着噪声和干扰，信源发出消息x，通过信道后信宿只可能收到由于干扰作用引起的某种变形的y。信宿收到y后推测信源发出x的 概率，这一过程可由 后验概率p(x|y)来描述。相应地，信源发出x的概率p(x)称为 先验概率。我们定义x的后验概率与先验概率比值的 对数为y对x的互信息量（简称互信息）。 [1]  

根据熵的连锁规则，有

因此，

这个差叫做X和Y的互信息，记作I(X;Y)。

按照熵的定义展开可以得到：

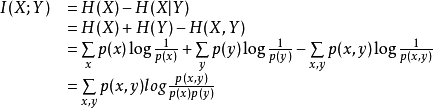
非负性

 

，且等号成立的充要条件是

   

和

   

相互独立。

链法则

数据处理不等式

如果

   

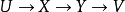构成马式链，则

 

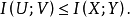
其他

某个词t和某个类别Ci传统的互信息定义如下:

互信息是 计算语言学模型分析的常用方法，它度量两个对象之间的相互性。在过滤问题中用于度量特征对于主题的 区分度。互信息的定义与交叉熵近似。互信息本来是 信息论中的一个概念,用于表示信息之间的关系, 是两个随机变量统计相关性的测度，使用互信息理论进行特征抽取是基于如下假设:在某个特定类别出现频率高,但在其他类别出现频率比较低的词条与该类的互信息比较大。通常用互信息作为特征词和类别之间的测度，如果特征词属于该类的话，它们的互信息量最大。由于该方法不需要对特征词和类别之间关系的性质作任何假设，因此非常适合于 文本分类的特征和类别的 配准工作。