线性回归算法梳理-Task3

回归评价指标MSE、RMSE、MAE、R-Squared

波士顿房产数据

1. 波士顿房产数据(只使用房间数量这个特征)

2. 数据切分（train_test_split）

3. MSE、MAE、RMSE、r2_score(自己写)VS scikit-learn中的MSE和MAE、r2_score

from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

boston = datasets.load_boston()
# print(boston.DESCR)       #获得关于房价的描述信息
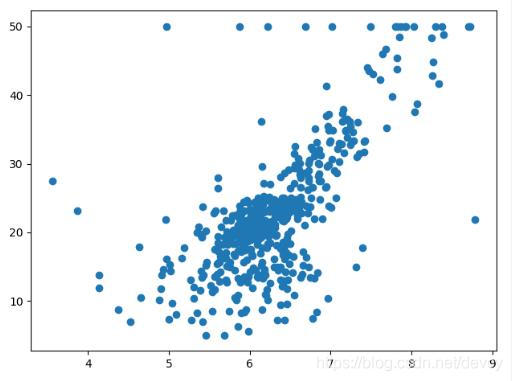
x = boston.data[:,5]  #得到RM列的数据
print(x.shape)
x = x.reshape(-1,1) #变为1列
y = boston.target
y = y.reshape(-1,1) #变为1列
print(y.shape)
plt.scatter(x, y)
plt.show()

x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.25,random_state = 0)
#创建线性回归模型
regr = LinearRegression()
#用训练集训练模型
regr.fit(x_train,y_train)
#用训练得出的模型进行预测
y_pred = regr.predict(x_test)

x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.25,random_state = 0)

mse_test = np.sum((y_pred-y_test)**2)/len(y_test)
mae_test = np.sum(np.absolute(y_pred-y_test))/len(y_test)
rmse_test = mse_test ** 0.5
r2_score = 1- (mse_test/ np.var(y_test))
print('均方误差:{},平均绝对误差:{},\n均方根误差:{},决定系数:{}'.format(mse_test,mae_test,rmse_test,r2_score))

from sklearn.metrics import mean_squared_error #均方误差
from sklearn.metrics import mean_absolute_error #平方绝对误差
from sklearn.metrics import r2_score #R square
#调用函数获得结果
mse_test1 = mean_squared_error(y_test,y_pred)
mae_test1 = mean_absolute_error(y_test,y_pred)
rmse_test1 = mse_test1 ** 0.5
r2_score1 = r2_score(y_test,y_pred)
print('均方误差:{},平均绝对误差:{},\n均方根误差:{},决定系数:{}'.format(mse_test1,mae_test1,rmse_test1,r2_score1))

参考文献
https://www.jianshu.com/p/9ee85fdad150 回归评价指标MSE、RMSE、MAE、R-Squared
https://blog.youkuaiyun.com/weixin_41043240/article/details/79587583 np.reshape里面的-1