The Core

最新推荐文章于 2024-10-17 16:03:45 发布

原创最新推荐文章于 2024-10-17 16:03:45 发布 · 247 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#博弈论

本文探讨了在博弈论中，核心玩家（Core Players）的概念及其重要性。核心玩家是在大型合作团队中不可或缺的角色，他们的存在确保了团队的稳定。文章通过举例说明，解释了如何确定是否存在核心玩家，并分析了团队是否愿意留在大团队的条件。此外，还讨论了convex game的概念，即团队联合的收益大于单独行动的总和，以及这种类型博弈的特征。最后，文章提出了一个问题：在现实世界中，人们是否倾向于参与有核心玩家的博弈，以及如何设计博弈规则以影响The Core的存在。

[1]Kevin Leyton-Brown (UBC), GTO-7-04: The Core, Nov 22, 2013, Game Theory Online, https://www.youtube.com/watch?v=DW_-I8UuU6I&list=PLeY-lFPWgBTif4PmLSN8eJsfOhFv_QUPl&index=4

[2]Matt Jackson (Stanford), GTO-7-05: Comparing the Core and the Shapley Value in an Example, Nov 22, 2013, Game Theory Online, https://www.youtube.com/watch?v=zmtFhP4cMhQ&list=PLeY-lFPWgBTif4PmLSN8eJsfOhFv_QUPl&index=5

【轉註】夏普利值（the Shapley value）定義了大團隊（grand coalition）的收益分配。

但人們是否願意留在大團隊？會不會更想要小團隊（smaller coalition），也許團隊總收入低些，但每個人分到的收益反而多。[1]

例如國會投票博弈中政黨A和政黨B合謀，故意讓投票失敗，然後這筆錢somehow到了兩黨面前，兩黨私下分，那麼兩黨可以分到比Shapley value更多的錢。這樣兩黨就有從大團隊背離出去成立小團隊的動力了。

那到底什麼條件下人們願意加入大團隊（grand coalition）呢？答案是：核心玩家在大團隊中。

如何定義核心玩家呢？

我們不看夏普利值了，我們來另外構造一個收益分配數組 $[x_1,x_2,...,x_n]$ ，參與者集合 $N=\{1,2,...,n\}$ ，參與者 $i$ 的收益分配額是 $x_i$ 。

和夏普利值一樣， $x_1+x_2+...+x_n=v(N) \text{\space \space}(1)$ 。 $v$ 是博弈價值函數，詳細定義見夏普利值（the Shapley Value）的定義和舉例，直覺理解可以是一次買賣的成交價，一次拍賣的成交價，企業的總收益。

對於任意小團體 $S(S\subseteq N)$ ，聯立不等式方程組：

$\sum_{i\in S}x_i\geq v(S)$

並同等式（1）。如果有解，就是有核心玩家，所有收益值 $x_i$ 可以為正數的參與者為核心玩家。

舉個例子，上面的投票博弈（Voting games），我們來計算The Core。

$x_1+x_2+x_3+x_4=100 \text{\space \space \space} (2)$

$x_1+x_2\geq v(\{1,2\})=100 \text{\space \space \space} (3)$

$x_1+x_2+x_3\geq v(\{1,2,3\})=100 \text{\space \space \space} (4)$

$x_2+x_3+x_4\geq v(\{2,3,4\})=100 \text{\space \space \space} (5)$

好了，我們不需要列出更多的不等式，已經可以看出無解。

(2)和(4)，推出 $x_4=0$ ；(2)和(5)，推出 $x_1=0$ ；(2)和(3)，推出 $x_3+x_4=0$ ，又 $x_4=0$ ，那麼 $x_3=0$ 。這樣等式(2)不成立。

這是數學嚴謹的方法，直覺地，為什麼這個博弈沒有核心玩家呢？因為能獲得收益的小團隊組合是 $\{1,2\},\{1,3\},\{1,4\},\{1,2,3\},\{1,2,4\},\{1,3,4\},\{2,3,4\}$ ，看起來前面的集合參與者 $1$ 都在，但最後一個集合沒有參與者 $1$ 。換句話說沒有一個玩家是成功的不可或缺的參與者。

換個投票規則，如果必須大於等於80%的人同意，決議才通過。那麼，成功的小團隊組合是 $\{1,2,3\},\{1,2,4\}$ ，參與者 $1$ 和 $2$ 是成功團隊的不可或缺的成員。我們來計算The Core以驗證。

$x_1+x_2+x_3+x_4=100 \text{\space \space \space} (6)$

$x_1+x_2+x_3\geq v(\{1,2,3\})=100 \text{\space \space \space} (7)$

$x_1+x_2+x_4\geq v(\{1,2,4\})=100 \text{\space \space \space} (8)$

解為 $x_1+x_2=100,x_3=0,x_4=0$ 。參與者3和4是成功必要的參與者，因為可被取代，在The Core中值為零。

我們來計算這種情況的每個參與者的夏普利值。

$\phi_1(N,v)=\phi_2(N,v)=\frac{1000}{24},\phi_3(N,v)=\phi_4(N,v)=\frac{200}{24}$

看另一個例子[2]， $S=\{1,2,3\}$ 。

我在想，是不是西方文化中核心玩家的概念是忌諱的，所以老師竭盡全力很委婉很含糊地傳達The Core的概念。

老師說當且僅當團隊中存在有一票否決權的參與者，存在The Core。其中無一票否決權的參與者payoff是0。

為什麼要將參與者模糊化成其收益值？參與者payoff為零列在The Core有什麼意思？分文不值。為什麼不索性說，分文不值的參與者沒有躋身The Core？

我們就簡單粗暴地認為：從不可或缺性來分配收益的話，核心玩家通吃。其他人能掙點小錢（夏普利值為正），但不在核心圈。

但這也說明，當我們遇到The Core這個概念，直覺反應是——這個博弈中隱性或顯性的有一票否決權的參與者。

（註：以下是我對The Core的疑惑。）

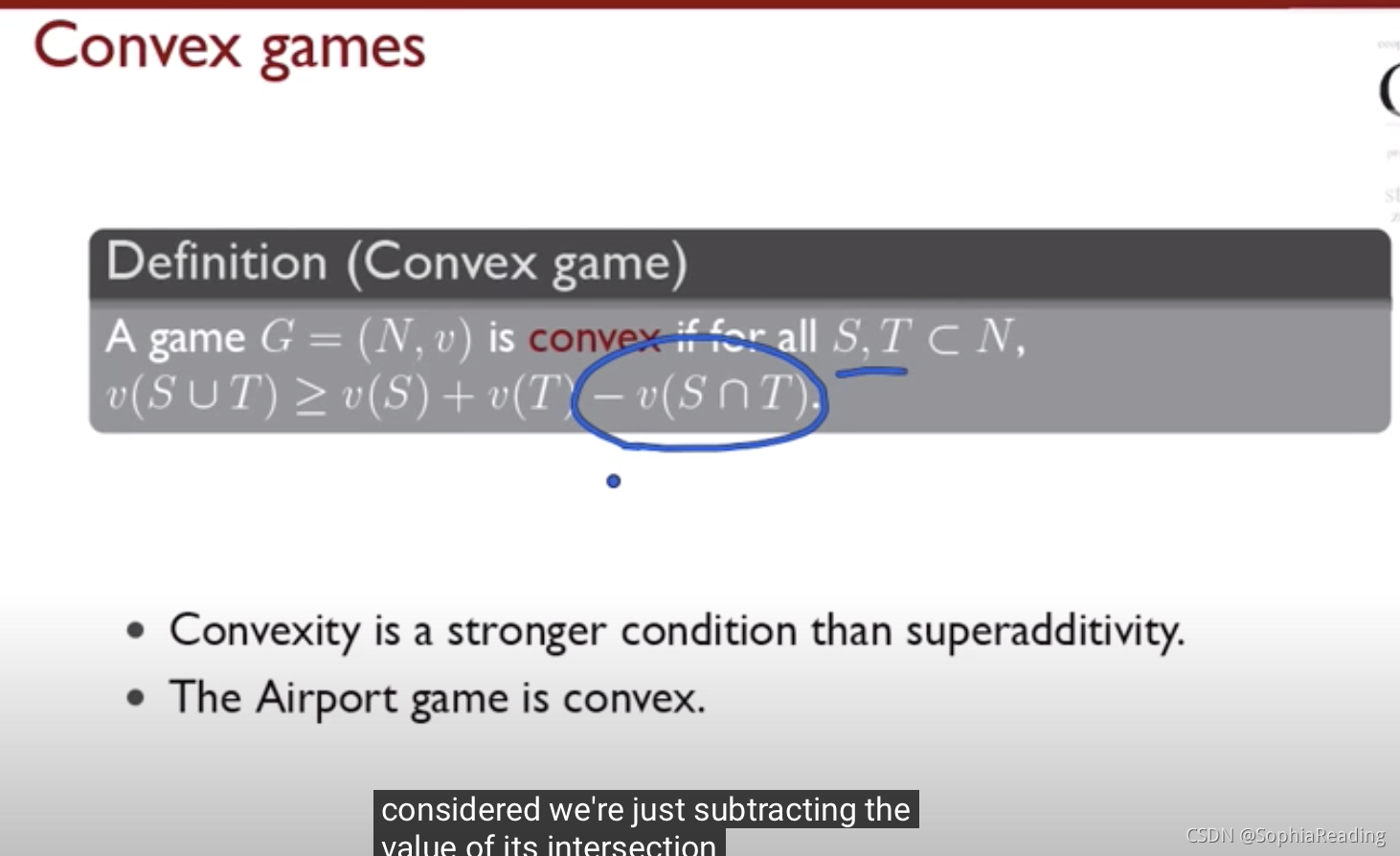
老師又定義convex game。convexity比優加性（superadditivity）還要嚴格，因為優加性認為S和T沒有交集，而convexity允許S和T有交集，且還要減去。就是博弈價值計算時，沒有水分。convex game的含義是兩個團隊聯合博弈的價值大於各自為戰的價值總和。老師說Airport game是convex game。

建機場的博弈（Airport Game）

幾個靠近的城市聯合建一個大機場好，還是各建一個小機場好？ $n$ 個城市為參與者， $N=\{1,2,...,n\}$ 。如果建一個大機場，其成本主要取決於最大的飛機的跑道。（這是真的嗎？跑道這麼貴嗎？）分攤成本的話，設建大機場總成本為 $na$ ，各建一個機場，成本為 $c_i$ 。 $v(\{i\})=c_i-a$ 。那確實滿足 $v(S\cup T)\geq v(S)+v(T)-v(S\cap T ), (S,T\subseteq N)$ 。