八大排序算法

插入排序

包括直接插入排序和希尔排序

直接插入排序

将一个记录插入到已排序好的有序表中，从而得到一个新，记录数增1的有序表。

直接插入排序最适合排序那些基本有序列表。

希尔排序

直接插入排序再排序基本有序列表非常之快。针对这一优点，shell提出了非常优秀的希尔排序算法。希尔排序也被称为缩小增量排序。
算法首先按照一定步长对数据进行分组，对每组进行插入排序，然后将步长折半，继续对每组进行插入排序，最后步长变为1，相当于对所有元素进行了一次插入排序。
希尔排序是一个典型的非常简单但是计算复杂度很难的算法。可以证明希尔排序的平均复杂度仅仅为n^1.3

选择排序

包括直接选择排序和堆排序

直接选择排序

在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比较为止。

堆排序

使用最大堆或者最小堆进行排序。先构建堆，然后一次弹出堆顶的元素。

交换排序

包括冒泡排序和快速排序

冒泡排序

在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。

快速排序

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

public static int partition(int []array,int lo,int hi){
        //固定的切分方式
        int key=array[lo];
        while(lo<hi){
            while(array[hi]>=key&&hi>lo){//从后半部分向前扫描
                hi--;
            }
            array[lo]=array[hi];
            while(array[lo]<=key&&hi>lo){从前半部分向后扫描
                lo++;
            }
            array[hi]=array[lo];
        }
        array[hi]=key;
        return hi;
    }

    public static void sort(int[] array,int lo ,int hi){
        if(lo>=hi){
            return ;
        }
        int index=partition(array,lo,hi);
        sort(array,lo,index-1);
        sort(array,index+1,hi); 
     }

归并排序

先将要排序的序列分成两个子序列，然后分别排序。然后将排序结果归并。递归完成所有排列。

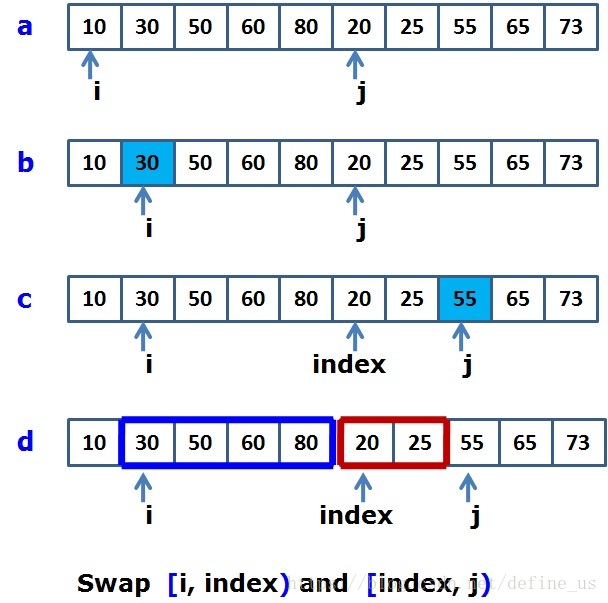
归并排序的难点在于原地归并。不使用辅助空间。这里面用到了所谓的手摇算法。

    public static void main(String[] args) {
        System.out.println("begin");
        int[] a = new int[]{2,4,5,2,3,
                6,12,21,23,34,
                32,12,9,27,87,
                23,31,2,4,5};
        //int[] a = new int[]{5,4,3,2,1};
        sort(a,0,a.length-1);
        for(int i:a){
            System.out.println(i);
        }

    }

    public static void sort(int[] a,int i,int j){
        if(i==j){
            return;
        }
        if(i==j-1){
            if(a[i]>a[j])swap(a, i, j);
            return;
        }

        int mid = i + (int)Math.floor((j-i)/2);
        sort(a,i,mid);
        sort(a,mid+1,j);
        int pre = i;
        int after = mid + 1;
        while (true){
            if(a[pre]<=a[after]){
                pre = pre + 1;
                if(pre>=after){
                    return;
                }
            }else{
                int index = after;
                while(true){
                    after = after + 1;
                    if(after>j){
                        swapSeg(a,pre,index-1,after-1);
                        return;
                    }
                    if(a[after]>a[pre]){
                        swapSeg(a,pre,index-1,after-1);
                        break;
                    }
                }
            }
        }

    }

    //利用手摇算法交换段
    public static void swapSeg(int[] a,int i,int index,int j){
        trans(a,i,index);
        trans(a,index+1,j);
        trans(a,i,j);
    }

    public static void trans(int[] a,int i,int j){
        int begin = i;
        int end = j;
        while (true){
            swap(a,begin,end);
            begin++;
            end--;
            if(begin==end || begin>end){
                return;
            }
        }
    }

    public static void swap(int[] a,int i,int j){
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

基数排序

也被称为桶排序。想象一下，给你一万个数，但是这一万个数只有1，2，3三个值，请问如何排序。显然你会把一万个分到1，2，3三个桶里，然后顺序排列即可。这也就是桶排序的原理。
桶排序不算是正统排序问题，因为他必须建立在所要排序的数值取值有限的先验知识上。

各种排序的性质总结如下图

排序的稳定性是指，相等的元素在排序前后会不会交换彼此的顺序。

排序的本质是什么？排序的本质是消除逆序数。两个数，位置和大小不匹配称为一个逆序数。消除逆序数最简单的就是比较相邻的两个元素，这样做只能是得到n^2的复杂度。希尔、快排、堆排都是希望可以比较比较远的两个数的大小。这样，才能偶尔通过一次比较，消除多于一个的逆序数。其实，他们只不过是消除逆序数选取的规则不同罢了。

附录

复杂度大小比较
O(1)
O(log2n)
o(nf)(f在幂次上，小于1)
O(n)
O(nlog2n)
O(n2)
O(n3)
O(nk)
O(2n)