图像处理：直方图均衡化原理与应用-优快云博客

本文链接：https://blog.youkuaiyun.com/deepinC/article/details/82793702

本文介绍了图像直方图的基本概念，阐述了直方图均衡化的理论，包括其目的、变换函数的性质，并通过示例展示了直方图均衡化的过程。此外，还探讨了直方图在图像增强中的应用，如通过灰度分布概率、平均值和方差来分析图像特征。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

基本概念

图像直方图：数字图像直方图是离散函数 $h(rk)=nk\mathcal{h}(r_k)=n_k$ ，其中 $r_k$ 是指第 $k$ 级灰度， $n_k$ 是图像中灰度级为 $r_k$ 的像素值的个数。若用图像中的每个灰度级对应的 $n_k$ 除以它的像素个数的总数，就是归一化的直方图。一般情况下，若图像的直方图成均匀分布态势，则图像的对比度会较高且有比较丰富的灰度色调。
直方图均衡：其目的是使得图像的灰度值分布尽可能地“均匀”的分布到各个级别，从而提高灰度对比，使得图像的视觉效果更好。具体如下实例：

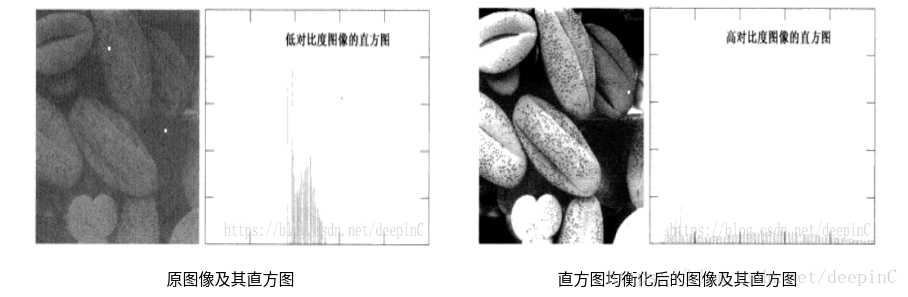
局部直方图均衡：将图像分成若干块，对每块单独作均衡处理

直方图均衡化理论证明

找到一个变换函数 $s = h (r)$ ，使得该函数具有如下性质：

单调递增——目的是为了”可逆/可还原“变换
$rand(h(r))∈[0,L−1]\text{rand}(h(r)) \in [0, L-1]$

即直方图均衡化的变换函数必须满足上述两个性质

注意到，若变换后的变量 $s$ 是一个具有均匀概率密度的随机变量时，则意味着有 $s$ 所生成的图像对应的直方图是均匀分布的，即均衡的。下面就要找到这样一个变换函数。
其实，存在如下变换： $\int_0^r{p_r(w)dw}，\tag{1}$
其中 $p_r(w)$ 为 $r$ 的概率密度函数。实质上，该变换函数 $T$ 是 $r$ 的累积概率分布函数，它一定是满足上述的两个性质的。同时，经过该变换后得到的随机变量 $s$ ，其概率密度函数也必定是均匀分布的。下面证明这一点：

因
$(2)dsdr=dT(r)dr=(L−1)ddr∫0rpr(w)dw=(L−1)pr(r)>0\frac{ds}{dr} = \frac{dT(r)}{dr} = (L - 1) \frac{d}{dr} \int_0^rp_r(w)dw = (L - 1) p_r(r) > 0 \tag{2}$
又由基本概率论可知，对于 $p_r(r)$ 和 $p_s(s)$ ，其各自表示随机变量 $r$ 和 $s$ 的概率密度函数， $s$ 为变换后的随机变量， $r$ 为变换前的随机变量，那么它们具有如下公式：
$(3)ps(s)=pr(r)∣drds∣p_s(s) = p_r(r) \left|\frac{dr}{ds}\right| \tag{3}$
故将（2）代入（3）可得：
$(4)ps(s)=pr(r)∣drds∣=pr(r)∣1(L−1)pr(r)∣=1L−1p_s(s) = p_r(r) \left|\frac{dr}{ds}\right| = p_r(r) \left|\frac{1}{(L - 1)p_r(r)}\right| = \frac{1}{L - 1} \tag{4}$
由（4）可得， $s$ 是一个具有均匀概率密度的随机变量。这意味着由 $s$ 生成的图像所对应的直方图是均匀分布的，变换函数 $T$ 即为直方图均衡变换函数

以上就是变换函数 $T$ 为什么可对直方图进行均衡化处理的理论证明，公式（1）即为连续情况下直方图均衡化的核心公式

直方图均衡化示例

下面举个例子来说明如何对二维离散图像进行直方图均衡化
给定如下 3×3 大小的图像，其灰度级别为 $[0, 3]$ ，即 $L = 4$ ：
$\left[\begin{array}{lll} 0 & 3 & 3 \\[.4em] 1 & 2 & 3 \\[.4em] 2 & 0 & 0 \end{array}\right]$
该图像的各个像素值 $r$ 对应的概率密度函数 $p_r(r)$ 为： $pr(0)=39,pr(1)=19,pr(2)=29,pr(3)=39p_r(0) = \displaystyle\frac{3}{9}, p_r(1) = \displaystyle\frac{1}{9}, p_r(2) = \displaystyle\frac{2}{9}, p_r(3) = \displaystyle\frac{3}{9}$ 。所以根据公式（1），其在离散变量下对应的输出像素 $s$ 为： $p_r(0) = 1, T(1) = 3 \displaystyle\sum_{i=0}^1{p_r(i)} = \displaystyle\frac{4}{3}， T(2) = 3 \displaystyle\sum_{i=0}^2{p_r(i)} = 2, T(3) = 3 \displaystyle\sum_{i=0}^3{p_r(i)} = 3$ ，故其均衡化后的输出图像为：
$\left[\begin{array}{lll} 1 & 3 & 3 \\[.4em] \displaystyle\frac{4}{3} & 2 & 3 \\[.8em] 2 & 1 & 1 \end{array}\right]$

在图像增强中使用直方图统计

涉及公式：

图像灰度分布概率： $p(ri)=nin,i=1,2,…,L−1p(r_i) = \displaystyle\frac{n_i}{n}, i=1,2,\dots,L-1$ ，其中 $n_i$ 表示灰度级为 $i$ 的像素点个数， $n$ 为总的像素点个数
图像灰度平均值： $\displaystyle\sum_{i=1}^{L-1}{r_i p(r_i)}$ —— 衡量图像整体是偏暗还是偏亮。若该值偏大，则说明偏亮；否则相反
图像灰度方差： $μ=∑i=1L−1(ri−m)2p(ri)\mu = \displaystyle\sum_{i=1}^{L-1}{(r_i - m)^2 p(r_i)}$ —— 衡量图像整体的灰度变化是否明显，即对比度是否高。若该值偏大，则说明对比度高；否则相反

具体应用例子：

如何判断图像的某个像素点是否处于边缘处？

取以该像素点为中心的一个领域，统计该领域内所有像素的方差 $μ\mu$ 。若 $μ\mu$ 偏大，则说明该像素点处于边缘处，否则不是
如何判断图像的某个像素点是否处于较黑暗处？

取以该像素点为中心的一个领域，统计该领域内所有像素的均值 $m$ 。若 $m$ 偏小，则说明该像素点处于偏暗处，否则不是