java之学习记录 11 - 1 - 数据结构与算法高级（红黑树）

红黑树

平衡二叉查找树

这种二叉查找树就退化成了链表，由于树的深度变得多了，查找的效率也会大幅下降

 

所以需要对这种二叉树进行自平衡，红黑树就是一种自平衡的二叉查找树。

 

红黑树（Red Black Tree）

除了二叉查找树 (BST) 的特征外，还有以下特征：

• 每个节点要么是黑色，要么是红色
• 根节点是黑色
• 每个叶子节点都是黑色的空结点（NIL结点）（为了简单期间，一般会省略该节点）
• 如果一个节点是红色的，则它的子节点必须是黑色的（父子不能同为红）
• 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点（平衡的关键）
• 新插入节点默认为红色，插入后需要校验红黑树是否符合规则，不符合则需要进行平衡

一颗典型的红黑树：

在对红黑树进行添加或者删除操作时可能会破坏这些特点，所以红黑树采取了很多方式来维护这些特点，从而维持平衡。主要包括：左旋转、右旋转和颜色反转

 

左旋（ RotateLeft ）

 

逆时针 旋转红黑树的两个结点，使得父结点被自己的右孩子取代，而自己成为自己的左孩子

上图所示过程如下：

• 1. 以X为基点逆时针旋转
• 2. X的父节点被x原来的右孩子Y取代
• 3. c保持不变
• 4. Y节点原来的左孩子c变成X的右孩子

右旋（ RotateRight ）

 

顺时针 旋转红黑树的两个结点，使得父结点被自己的左孩子取代，而自己成为自己的右孩子

上图所示过程如下：

• 1. 以X为基点顺时针旋转
• 2. X的父节点被x原来的左孩子Y取代
• 3. b保持不变
• 4. Y节点原来的右孩子c变成X的左孩子

颜色反转

 

就是当前节点与父节点、叔叔节点同为红色，这种情况违反了红黑树的规则，需要将红色向祖辈上传，父节点和叔叔节点红色变为黑色，爷爷节点从黑色变为红色（爷爷节点必为黑色，因为此前是符合红黑树规则的）。这样每条叶子结点到根节点的黑色节点数量并未发生变化，因此都其他树结构不产生影响

红黑树插入有五种情况，每种情况对应着不同的调整方法：

 

1. 新结点（ A ）位于树根，没有父结点

直接让新结点变色为黑色，规则 2 得到满足。同时，黑色的根结点使得每条路径上的黑色结点数目都增加了1 ，所以并没有打破规则 5

2. 新结点（ B ）的父结点是黑色

新插入的红色结点 B 并没有打破红黑树的规则，所以不需要做任何调整

3. 新结点（ D ）的父结点和叔叔结点都是红色

两个红色结点 B 和 D 连续，违反了规则 4 。因此先让结点 B 变为黑色

这样一来，结点 B 所在路径凭空多了一个黑色结点，打破了规则 5 。因此我们让结点 A 变为红色

结点 A 和 C 又成为了连续的红色结点，再让结点 C 变为黑色

经过上面的调整，这一局部重新符合了红黑树的规则

 

4. 新结点（ D ）的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的右孩子，父结点（B ）是祖父结点的左孩子

 

以结点 B 为轴，做一次左旋转，使得新结点 D 成为父结点，原来的父结点 B 成为 D 的左孩子

这样进入了情况 5

 

5. 新结点（ D ）的父结点是红色，叔叔结点是黑色或者没有叔叔，且新结点是父结点的左孩子，父结点（B ）是祖父结点的左孩子

 

以结点 A 为轴，做一次右旋转，使得结点 B 成为祖父结点，结点 A 成为结点 B 的右孩子

接下来，让结点 B 变为黑色，结点 A 变为红色

经过上面的调整，这一局部重新符合了红黑树的规则

 

红黑树构建过程

 

如下图：

上图所示过程如下：

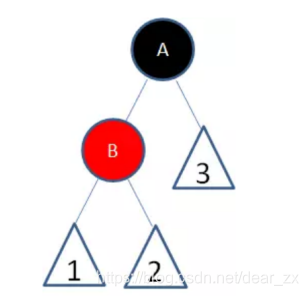
1. 新插入节点默认为红色，5<10，插入到左子节点，插入后左子树深度为2（叶子节点黑色+根节点黑色），右子树深度为也是2（叶子节点黑色+根节点黑色），满足红黑树规则。

2. 新插入节点为红色，9<10，需要在左子树进行插入，再和5比较，大于5，放到5的右子树中，此时各个叶子节点到根节点的深度依然是2，但5和9两个节点都是红色，不满足规则第4条，需要进行左旋、右旋操作，使其符合规则。可以看出经过操作后，左右子树又维持了平衡。

上图所示过程如下：

1. 插入节点3后，可以看到又不符合红黑树的规则了，而此时的情况，需要采用颜色反转的操作，就是把5、10两个节点变为黑色，5、10的父节点变为红色，但父节点9是根节点，不能为红色，于是再将9变为黑色，这样整个树的深度其实增加了1层。

2. 继续插入6节点，对树深度没有影响。

3. 插入7节点后，6、7节点都为红节点，不满足规则4，需要进行颜色反转调整，也就是7的父节点和叔叔节点变为黑色，爷爷节点5变为红色。

上图所示过程如下：

1. 继续插入节点19，对树深度没有影响，红黑树的规则都满足，无需调整。

2. 插入节点32后，又出现了不满足规则4的情况，此时节点32没有叔叔节点，如果颜色反转的话，左右子树的深度就出现不一致的情况，所以需要对爷爷节点进行左旋操作。

3. 父节点取代爷爷节点的位置，父节点变为黑色，爷爷节点变为父节点的左子树变为红色。

上图所示过程如下：

1. 插入节点24后，红黑树不满足规则4，需要调整。

2. 此时父节点32和叔叔节点10都为红色，需要进行颜色反转，爷爷节点19变为红色，父节点、叔叔节点变为黑色，颜色反转树的深度不发生变化。

上图所示过程如下：

1.插入节点17后，未破坏红黑树规则，不需要调整。

代码实现

/**
* 红黑树结点
*/
public class RBTreeNode {
    private int key;
    private boolean isBlack;
    private RBTreeNode left;
    private RBTreeNode right;
    private RBTreeNode parent;
    public RBTreeNode(int key) {
        this.key = key;
        this.isBlack = false; //新节点默认是红色
    }
    public int getKey() {
        return key;
    }
    public boolean isBlack() {
        return isBlack;
    }
    public RBTreeNode getLeft() {
        return left;
    }
    public RBTreeNode getRight() {
        return right;
    }
    public RBTreeNode getParent() {
        return parent;
    }
    public void setKey(int key) {
        this.key = key;
    }
    public void setBlack(boolean black) {
        isBlack = black;
    }
    public void setLeft(RBTreeNode left) {
        this.left = left;
    }
    public void setRight(RBTreeNode right) {
        this.right = right;
    }
    public void setParent(RBTreeNode parent) {
        this.parent = parent;
    }
    @Override
    public String toString() {
        return "RBTreeNode{" +
            "key=" + key +
            ", color=" + (isBlack==true?"BLACK":"RED") +
            '}';
    }
}



/**
* 红黑树
*/
public class RBTree {
    RBTreeNode root; //根节点
    /**
    * 遍历节点
    *
    */
    public void list(RBTreeNode node) {
        if(node==null) return ;
        //叶子
        if(node.getLeft()==null&&node.getRight()==null){
            System.out.println(node);
            return ;
        }
        System.out.println(node);
        //递归 左孩子
        list(node.getLeft());
        //递归 右孩子
        list(node.getRight());
    }
    public void insert(int key) {
        RBTreeNode node = new RBTreeNode(key);
        if (root == null) {
            node.setBlack(true);//根是黑色的
            root = node;
            return;
        }
        RBTreeNode parent = root;
        RBTreeNode son = null;
        if (key <= parent.getKey()) {
            son = parent.getLeft();
        } else {
            son = parent.getRight();
        }
        //find the position
        while (son != null) {
            parent = son;
            if (key <= parent.getKey()) {
                son = parent.getLeft();
            } else {
                son = parent.getRight();
            }
        }
        if (key <= parent.getKey()) {
            parent.setLeft(node);
        } else {
            parent.setRight(node);
        }
        node.setParent(parent);
        // 自平衡
        banlanceInsert(node);
    }
    /**
    * 自平衡
    *
    * @param node
    */
    private void banlanceInsert(RBTreeNode node) {
        RBTreeNode father, grandFather;
        while ((father = node.getParent()) != null && father.isBlack() == false)
        {
            grandFather = father.getParent();
            //父为祖左孩子
            if (grandFather.getLeft() == father) {
                RBTreeNode uncle = grandFather.getRight();
                if (uncle != null && uncle.isBlack() == false) {
                    setBlack(father);
                    setBlack(uncle);
                    setRed(grandFather);
                    node = grandFather;
                    continue;
                }
                if (node == father.getRight()) {
                    //左旋
                    leftRotate(father);
                    RBTreeNode tmp = node;
                    node = father;father = tmp;
                }
                setBlack(father);
                setRed(grandFather);
                //右旋
                rightRotate(grandFather);
            }
            //父为祖右孩子
            else {
                RBTreeNode uncle = grandFather.getLeft();
                if (uncle != null && uncle.isBlack() == false) {
                    setBlack(father);
                    setBlack(uncle);
                    setRed(grandFather);
                    node = grandFather;
                    continue;
                }
                if (node == father.getLeft()) {
                    //右旋
                    rightRotate(father);
                    RBTreeNode tmp = node;
                    node = father;
                    father = tmp;
                }
                setBlack(father);
                setRed(grandFather);
                //左旋
                leftRotate(grandFather);
            }
        }
        setBlack(root);
    }
    /**
    * 左旋
    *
    * @param node
    */
    private void leftRotate(RBTreeNode node) {
        RBTreeNode right = node.getRight();
        RBTreeNode parent = node.getParent();
        if (parent == null) {
            root = right;
            right.setParent(null);
        } else {
            if (parent.getLeft() != null && parent.getLeft() == node) {
                parent.setLeft(right);
            } else {
                parent.setRight(right);
            }
            right.setParent(parent);
        }
        node.setParent(right);
        node.setRight(right.getLeft());
        if (right.getLeft() != null) {
            right.getLeft().setParent(node);
        }
        right.setLeft(node);
    }
    /**
    * 右旋
    *
    * @param node
    */
    private void rightRotate(RBTreeNode node) {
        RBTreeNode left = node.getLeft();
        RBTreeNode parent = node.getParent();
        if (parent == null) {
            root = left;
            left.setParent(null);
        } else {
            if (parent.getLeft() != null && parent.getLeft() == node) {
                parent.setLeft(left);
            } else {
                parent.setRight(left);
            }
            left.setParent(parent);
        }
        node.setParent(left);
        node.setLeft(left.getRight());
        if (left.getRight() != null) {
            left.getRight().setParent(node);
        }
        left.setRight(node);
    }
    private void setBlack(RBTreeNode node) {
        node.setBlack(true);
    }
    private void setRed(RBTreeNode node) {
        node.setBlack(false);
    }
    public static void main(String[] args) {
        RBTree rb=new RBTree();
        rb.insert(10);//根节点
        rb.insert(5);
        rb.insert(9);
        rb.insert(3);
        rb.insert(6);
        rb.insert(7);
        rb.insert(19);
        rb.insert(32);
        rb.insert(24);
        rb.insert(17);
        rb.list(rb.root);
    }
}

时间复杂度 ： O(logn)

应用

在 JDK1.8 中 HashMap 使用数组 + 链表 + 红黑树的数据结构。内部维护着一个数组 table ，该数组保存着每个链表的表头结点或者树的根节点。HashMap 存储数据的数组定义如下，里面存放的是 Node<K,V> 实体：

 

transient Node<K, V>[] table;//序列化时不自动保存 

/*** 桶的树化阈值：即 链表转成红黑树的阈值， * 在存储数据时，当链表长度 > 该值时，则将链表转换 成红黑树 */ 

static final int TREEIFY_THRESHOLD = 8;