目录-动态规划问题整理

介绍

本篇文章为大熊个人的动规笔记，非算法教程。

技巧性总结

从台阶看分析动规时候的误区

要注意分清楚
有时候会傻逼的认为
那么取决于n-1，是不是f(n) = f(n-1) +1 …但是这是方法数，不是路径长度，事实上如果只考虑前进一步的话，f(n)与f(n-1)是同一条的路径达到的，所以其实是同一个方法。我们看，这其实是一颗多叉决策树

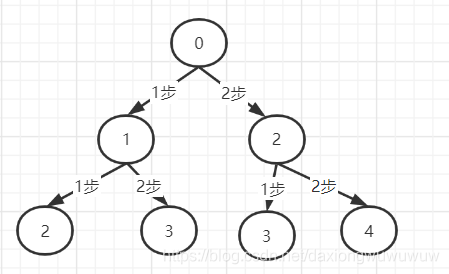
也就是说，我们事实上求得是这颗树的一个分支条数（方法），而非到达该分支的时候的步数（路程），比如达到2的方法树，其实我们看的只有条数，而不是节点数

很明显，上面只有两条。那么下面的1-2-3台阶其实也是一样的道理。如果要是求路径数，也就是节点长度，那么肯定会有个最值

初始化的时候该初始化到多少？

根据dp公式

比如dp[i] = dp[i-3] + dp[i-2]+dp[i-1] i减去的那个最大有3，那么应该初始化到3才能保证dp[i-3]取到i0

一般的矩形

一般二维数组需要初始化可以做出选择的两列，详见矩阵路径。

打印dp数组

刷题总结时候一定要记得打印dp数组，不然写了也是白写。比如刷leetcode的时候像这样打印出来

题目类型

台阶与矩阵

大熊的动态规划-台阶与矩阵笔记

背包

背包就是:能背负的重量为Wb
物品也有自己的重量Wg ，以及自己的价值Vg，然后用背包装东西求价值最大

牛客网 0-1 背包问题

题目：

借用一下算法大神labuladong的框架

for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 择优(选择1，选择2...)

我自行修改一下以上框架

for X1 in X1的所有取值：
    for X2 in X2的所有取值：
        for ...
            dp[X][X2][...] = 择优(选择1，选择2...)

X1、X2…Xn均为变量，dp[X1][X2]的值为y
那么我们看看01背包中的x和y都有哪些
首先有一下的变量
y我们先确定，y就是价值，我们要求的就是价值
那么x可以从如下几个地方取

a.物品两个属性，物品单个价值不算，因为y就是总价值，同个维度，所以应该取物品的个数。
b.背包的重量范围 ,这个肯定是x
那么就是y=dp[a][b]，当背包重量为b，物品个数为a的时候，y就是这个时候背包物品的最大价值。

那么接下来我们的代码将会是这样的

int dp[a][b]
for(int[] row:dp){
	Arrays.fill(row,-1)
}
for i in [1..a]:
   for j in [1..b]:
         //判断;如果物品放不进去背包
         //物品可以放进背包
        dp[i][j] = max（把物品装入背包，不把物品加入背包）
return dp[i][j]

问题来了，什么他么的叫把物品装入背包？做选择的时候一定要牢记dp的定义！
dp是什么，重量为a，个数为b的时候的最大值，什么的最大值？价值！
不装把
好，dp[i][j] = dp[i]-1[j] 反正重量j一定的情况下要不要这个东西都一样
装把
好 dp[i][j] = dp[i-1[j-物品重量]+物品价值。这时候i和j都在变。
这时候我们处理一下代码,感觉牛客网的判定有点问题，不管了。

public class Main {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 计算01背包问题的结果
     * @param V int整型 背包的体积
     * @param n int整型 物品的个数
     * @param vw int整型二维数组 第一维度为n,第二维度为2的二维数组,vw[i][0],vw[i][1]分别描述i+1个物品的vi,wi
     * @return int整型
     */
    
    public int knapsack (int V, int n, int[][] vw) {
        // write code here
        if(V==0 || n==0 || vw==null){
            return 0;
        }
        int[][] dp=new int[n+1][V+1];
        for(int i=1;i<=n;i++){
            for(int j=1;j<=V;j++){
                if(j<vw[i-1][0]){
                    dp[i][j]=dp[i-1][j];
                }
                else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-vw[i-1][0]]+vw[i-1][1]);
                }
            }
        }
        return dp[n][V];
    }
}

494. 目标和

leetcode416 分割等和子集

这个问题也是一个背包的问题。
分割两个等和子集也就是把数字塞进容量为sum/2为容量的背包。
那么设置dp[n][m]，物品个数是n,背包容量是m
y=dp[n][m]，代表着前n个物品，能不能正好装满容量为m的背包
那么怎么考虑base case呢？
当n为0，m不是0的时候，没有东西，那肯定不行。为false
当n不为0，m为0的时候，有东西和一个容量为0的背包，不用填东西就能“装满”，这行。
那么对于一个物品来说，它也只有三种情况，放得进去（放或者不放）或者不放
【！！！！！！】我们的代码是这样的:这里要特别特别！！！！！！！！！！！注意
dp的初始数组设置！！！！我之前设置为dp[n][m]，那是不对的！！！应该是dp[n+1][m+1]为什么？因为确实有物品为0，空背包的情况存在，n的取值范围是0-N，m同理，都是双闭合空间！。

class Solution {
    public boolean canPartition(int[] nums) {
        //边界条件，如果和是奇数就没必要在这判断了。
        int sum = 0;
        for(int num:nums){
            sum+=num;
        }
        if(sum%2==1){
            return false;
        }
        //不是奇数，开启背包
        int half = sum/2;
        boolean[][] dp = new boolean[nums.length+1][half+1];
        //处理base case
        for(boolean[] row:dp){
            Arrays.fill(row,false);
        }
        for(int i=0;i<nums.length;i++){
            dp[i][0] = true;
        }
        //处理背包
        for(int i=1;i<=nums.length;i++){
            for(int w=1;w<=half;w++){
                if(nums[i-1]>w){//物品放不进背包
                    dp[i][w] = dp[i-1][w];
                }else{                 
                    dp[i][w] =
                        (dp[i-1][w-nums[i-1]]) || //加入背包,能不能完全放满的情况和dp[i-1][w-nums[i]]是一样的
                        (dp[i-1][w]);//不加入背包,可能相同重量i-1个物品就能放满 ;
                }
            }
        }
        return dp[nums.length][half];

    }
}

leercode518 零钱兑换2

这是个无限的背包问题，也就是说固定的背包，无限的物品

定义dp。y=dp[amount+1][coins.length+1].因为同时存在amount和coin均可以是0的情况呢。
然后这里有个奇葩的设定，当金额为0的时候，并不是没有方法可以凑出来，而是有一种方法可以“凑”出来，也就是不凑，所以会有dp[0][i]=1这种骚操作。然后推导公式的时候我推导错误了。。
我推导成了这个
dp[i][j] = dp[i-coins[j-1]][j] + dp[i][j-1]+1
因为我想着，这个数字放进去的话，那么就是凑成i-coins[j-1]这个金额再加一个金币即可，然后我就加一。。但是我忘记了
题目求得是组合数不是硬币数
首先组合数，比如我有1，2 两个硬币，每种硬币无限个。比如说
【1】组成2的方法有两种！[2] 以及[1,1]
【2】那么组成3的方法呢？如果我加一就是三种，但是事实上，只是
[2] 和[1,1] 变成了 [2,1],[1,1,1],大家多加了一枚1块钱的硬币所以组合数不变，硬币的数量变了，正确的组合数应该是
dp[i][j] = dp[i-coins[j-1]][j] + dp[i][j-1]

class Solution {
    public int change(int amount, int[] coins) {
        //y=dp[amount+1][coins.length+1]
        int[][] dp = new int[amount+1][coins.length+1]; //金额为amount，硬币组合为0--coins.length情况下可以凑成金额为amount的组合树
        //basecase,金额是0，[错]没有方式可以凑,一种方式可以凑那就是都不放。。没有硬币没有方法可以凑
        for(int i=0;i<dp[0].length;i++){
            dp[0][i] = 1;
        }
        for(int i=1;i<=amount;i++){
            for(int j=1;j<=coins.length;j++){
                if(coins[j-1]>i){
                    dp[i][j] = dp[i][j-1];//这枚硬币放不进去
                }else{
                    //dp[i][j] = dp[i-coins[j-1]][j] + dp[i][j-1]+1 ;//可以放进去+可以不放进去，错误的推导公式
                    dp[i][j] = dp[i-coins[j-1]][j] + dp[i][j-1];
                }
            }
        }
        return dp[amount][coins.length]; 
    }
}

子序列

大熊的子序列笔记

剪绳子

大熊的剪绳子笔记