BZOJ 1711 吃饭dining/Luogu P1402 酒店之王 拆点+最大流流匹配

题意：

　　（吃饭dining）有F种食物和D种饮料，每种食物或饮料只能供一头牛享用，且每头牛只享用一种食物和一种饮料。现在有n头牛，每头牛都有自己喜欢的食物种类列表和饮料种类列表，问最多能使几头牛同时享用到自己喜欢的食物和饮料。（1 <= f <= 100, 1 <= d <= 100, 1 <= n <= 100）

 

　　（酒店之王）XX酒店的老板想成为酒店之王，本着这种希望，第一步要将酒店变得人性化。由于很多来住店的旅客有自己喜好的房间色调、阳光等，也有自己所爱的菜，但是该酒店只有p间房间，一天只有固定的q道不同的菜。

有一天来了n个客人，每个客人说出了自己喜欢哪些房间，喜欢哪道菜。但是很不幸，可能做不到让所有顾客满意（满意的条件是住进喜欢的房间，吃到喜欢的菜）。

这里要怎么分配，能使最多顾客满意呢？

 

分析：
　　我们想想发现，这两道题并没什么不同，都是一些人，一些东西，分别喜欢两类东西中的一些，每人只能占有两类中的各一样东西，问如何安排，让更多的人满意。

　　倘若只有一类东西，也许我们会想到二分图匹配。

　　但是两样东西，建二分图我们是建不出来的，所以只能藉由网络流来解决匹配问题，我们依旧是考虑题目中的限制问题：

　　首先限制1.喜欢两类东西中的各一些。

　　限制2.每人只能在两类中各占有一样东西。

　　我们发现限制不多，所以建图也没那么复杂。我们一单位的流量当然是代表一样东西。

　　我们怎么建出满足限制2的图？

　　引出一个拆点技巧，我们将人拆成两个点，我们保证这两个点之间的流量最大是1，所以一个人最多选一样东西。

　　所以我们把图简称这样：

　　

 

 

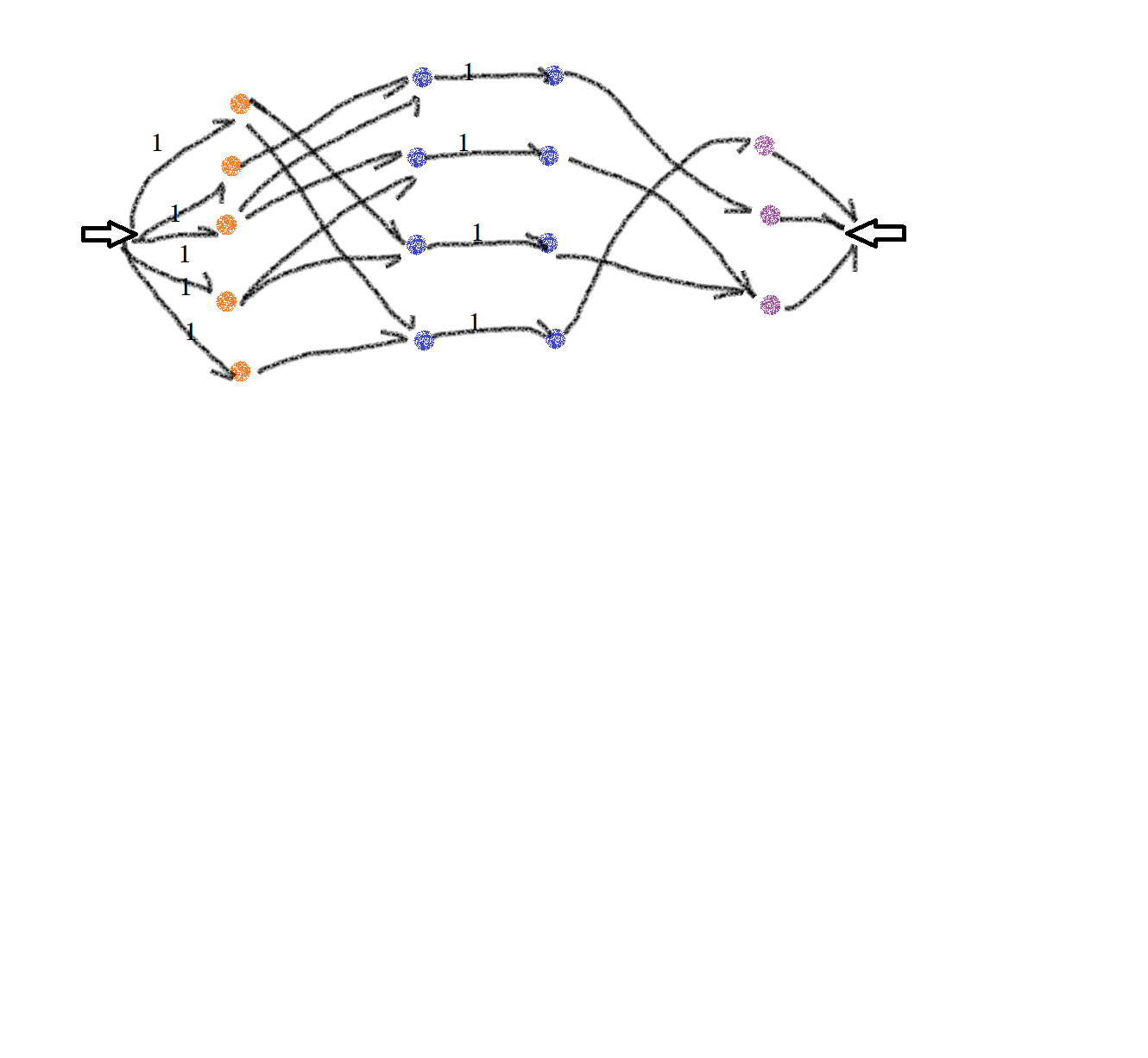
图丑请不要在意这些细节2333

　　蓝色的点代表人，橙色代表第一类物品，紫色代表第二类物品，边容量都是1.

　　只不过源点向第一类物品连边，第一类物品向喜欢它的人的一号店连边，人的一号点向二号点连边，人的二号点向他喜欢的第二类物品连边，第二类物品向汇点连边即可。这样，一单位流量流经一个人的两个点，代表被这个人选择了。

　　两道题几乎一模一样，都不用改数据范围，改改主函数就好了

代码：

 1 #include<bits/stdc++.h>
 2 #define ms(a,x) memset(a,x,sizeof(a))
 3 using namespace std;int tot=0;
 4 const int N=10005,inf=0x3f3f3f3f;
 5 struct node{int y,z,nxt;}e[N*2];
 6 int S,T,q[N],h[N],c=1,n,m,k,d[N];
 7 int c1[N],ho[N],di[N],c2[N];
 8 int add(int x,int y,int z){
 9     e[++c]=(node){y,z,h[x]};h[x]=c;
10     e[++c]=(node){x,0,h[y]};h[y]=c;
11 } bool bfs(){
12     int f=1,t=0;ms(d,-1);
13     q[++t]=S;d[S]=0;
14     while(f<=t){
15         int x=q[f++];
16         for(int i=h[x],y;i;i=e[i].nxt)
17         if(d[y=e[i].y]==-1&&e[i].z)
18         d[y]=d[x]+1,q[++t]=y;
19     } return (d[T]!=-1);
20 } int dfs(int x,int f){
21     if(x==T) return f;int w,tmp=0;
22     for(int i=h[x],y;i;i=e[i].nxt)
23     if(d[y=e[i].y]==d[x]+1&&e[i].z){
24         w=dfs(y,min(e[i].z,f-tmp));
25         if(!w) d[y]=-1;
26         e[i].z-=w;e[i^1].z+=w;
27         tmp+=w;if(tmp==f) return f;
28     } return tmp;
29 } void dinic(){
30     while(bfs()) tot+=dfs(S,inf);
31 } int main(){
32     scanf("%d%d%d",&n,&m,&k);
33     S=0,T=n*2+m+k+1;
34     for(int i=1;i<=m;i++) ho[i]=i;
35     for(int i=1;i<=n;i++) c1[i]=i+m;
36     for(int i=1;i<=k;i++) di[i]=n+m+i;
37     for(int i=1;i<=n;i++) c2[i]=n+m+k+i;
38     for(int i=1;i<=m;i++) add(S,ho[i],1);
39     for(int i=1;i<=k;i++) add(di[i],T,1);
40     for(int i=1;i<=n;i++) add(c1[i],c2[i],1);
41     for(int i=1,u,v;i<=n;i++){
42         scanf("%d%d",&u,&v);
43         for(int j=1,p;j<=u;j++) 
44         scanf("%d",&p),add(ho[p],c1[i],1);
45         for(int j=1,p;j<=v;j++) 
46         scanf("%d",&p),add(c2[i],di[p],1);
47     } dinic();printf("%d\n",tot);return 0;
48 }

吃饭dining

 1 #include<bits/stdc++.h>
 2 #define ms(a,x) memset(a,x,sizeof(a))
 3 using namespace std;int tot=0;
 4 const int N=10005,inf=0x3f3f3f3f;
 5 struct node{int y,z,nxt;}e[N*2];
 6 int S,T,q[N],h[N],c=1,n,m,k,d[N];
 7 int c1[N],ho[N],di[N],c2[N];
 8 int add(int x,int y,int z){
 9     e[++c]=(node){y,z,h[x]};h[x]=c;
10     e[++c]=(node){x,0,h[y]};h[y]=c;
11 } bool bfs(){
12     int f=1,t=0;ms(d,-1);
13     q[++t]=S;d[S]=0;
14     while(f<=t){
15         int x=q[f++];
16         for(int i=h[x],y;i;i=e[i].nxt)
17         if(d[y=e[i].y]==-1&&e[i].z)
18         d[y]=d[x]+1,q[++t]=y;
19     } return (d[T]!=-1);
20 } int dfs(int x,int f){
21     if(x==T) return f;int w,tmp=0;
22     for(int i=h[x],y;i;i=e[i].nxt)
23     if(d[y=e[i].y]==d[x]+1&&e[i].z){
24         w=dfs(y,min(e[i].z,f-tmp));
25         if(!w) d[y]=-1;
26         e[i].z-=w;e[i^1].z+=w;
27         tmp+=w;if(tmp==f) return f;
28     } return tmp;
29 } void dinic(){
30     while(bfs()) tot+=dfs(S,inf);
31 } int main(){
32     scanf("%d%d%d",&n,&m,&k);
33     S=0,T=n*2+m+k+1;
34     for(int i=1;i<=m;i++) ho[i]=i;
35     for(int i=1;i<=n;i++) c1[i]=i+m;
36     for(int i=1;i<=k;i++) di[i]=n+m+i;
37     for(int i=1;i<=n;i++) c2[i]=n+m+k+i;
38     for(int i=1;i<=m;i++) add(S,ho[i],1);
39     for(int i=1;i<=k;i++) add(di[i],T,1);
40     for(int i=1;i<=n;i++) add(c1[i],c2[i],1);
41     for(int i=1;i<=n;i++)
42     for(int j=1,p;j<=m;j++)
43     scanf("%1d",&p),p?add(ho[j],c1[i],1):0;
44     for(int i=1;i<=n;i++)
45     for(int j=1,p;j<=k;j++)
46     scanf("%1d",&p),p?add(c2[i],di[j],1):0;
47     dinic();printf("%d\n",tot);return 0;
48 }

酒店之王

 

转载于:https://www.cnblogs.com/Alan-Luo/p/10242406.html